矩阵,学过线性代数的都知道,矩阵满足结合律,但不满足交换律
关于矩阵,有很多经典的应用,可以看下大牛的博客http://www.matrix67.com/blog/archives/276
下面的题目中,最常见的一种应用就是利用矩阵求递推式,可以通过构造矩阵求幂
在这方面,最常见的就是在斐波那契数列方面,可以看下这个博客,超牛的http://www.cnblogs.com/Knuth/archive/2009/09/04/1559951.html
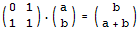 很容易构造出关于斐波那契的矩阵,累乘求幂,就可以求出斐波那契的对应的项
很容易构造出关于斐波那契的矩阵,累乘求幂,就可以求出斐波那契的对应的项
直接开始题目吧
题目,直接矩阵求幂,再求该矩阵的迹,注意,利用矩阵乘法满足结合律,我看可以利用二进制优化求幂次数。比如:A^7=A^4 * A^2 * A^1
具体的结合代码很容易理解的
 View Code
View Code
#include<iostream>
#include<algorithm>
#include<string>
using namespace std;
const int MOD = 9973;
const int N = 11;
int ret[N][N],init[N][N],temp[N][N];
int n;
void init_()
{
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
ret[i][j]=(i==j);
}
void matmul(int a[][N],int b[][N])
{
memset(temp,0,sizeof(temp));
for(int i=0;i<n;i++)
for(int k=0;k<n;k++)
if(a[i][k])
for(int j=0;j<n;j++)
if(b[k][j])
temp[i][j]=(temp[i][j]+a[i][k]*b[k][j])%MOD;
memcpy(a,temp,sizeof(temp));
}
void q_mod(int k)
{
init_();
for(;k;k>>=1)
{
if(k&1)
matmul(ret,init);
matmul(init,init);
}
}
int main()
{
int T,k;
scanf("%d",&T);
while(T--)
{
scanf("%d %d",&n,&k);
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
scanf("%d",&init[i][j]);
q_mod(k);
int ans=0;
for(int i=0;i<n;i++)
ans=(ans+ret[i][i])%MOD;
printf("%d\n",ans);
}
return 0;
}
题目:很明显的递推式求值,与斐波那契数列很类似,只需要重新构造一下矩阵A=
A B
1 0
向量a=(1,1),则当n大于2 时,f(n)=A^(n-2) * a
 View Code
View Code
#include<iostream>
#include<algorithm>
#include<string>
using namespace std;
const int MOD = 7;
const int N = 2;
int ret[N][N],init[N][N],temp[N][N];
int n;
void init_()
{
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
ret[i][j]=(i==j);
}
void matmul(int a[][N],int b[][N])
{
memset(temp,0,sizeof(temp));
for(int i=0;i<n;i++)
for(int k=0;k<n;k++)
if(a[i][k])
for(int j=0;j<n;j++)
if(b[k][j])
temp[i][j]=(temp[i][j]+a[i][k]*b[k][j])%MOD;
memcpy(a,temp,sizeof(temp));
}
void q_mod(int k)
{
init_();
for(;k;k>>=1)
{
if(k&1)
matmul(ret,init);
matmul(init,init);
}
}
int main()
{
int a,b,k;
n=2;
while(scanf("%d %d %d",&a,&b,&k)==3 && (a||b||k))
{
init[0][0]=a,init[0][1]=b;
init[1][0]=1,init[1][1]=0;
if(k<3)
{
printf("1\n");
continue;
}
k-=2;
q_mod(k);
int ans=(ret[0][0]+ret[0][1])%MOD;
printf("%d\n",ans);
}
return 0;
}
构造如下矩阵即可解决问题咯,很清晰

 View Code
View Code
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 10;
int n=10,mod;
int ret[N][N],init[N][N],temp[N][N];
void init_()
{
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
ret[i][j]=(i==j);
}
void matmul(int a[][N],int b[][N])
{
memset(temp,0,sizeof(temp));
for(int i=0;i<n;i++)
for(int k=0;k<n;k++)
if(a[i][k])
for(int j=0;j<n;j++)
if(b[k][j])
temp[i][j]=(temp[i][j]+a[i][k]*b[k][j])%mod;
memcpy(a,temp,sizeof(temp));
}
void q_mod(int k)
{
init_();
for(;k;k>>=1)
{
if(k&1)
{
matmul(ret,init);
}
matmul(init,init);
}
}
int main()
{
int k;
while(scanf("%d %d",&k,&mod)==2)
{
for(int i=0;i<n;i++)
scanf("%d",&init[0][i]);
if(k<10)
{
printf("%d\n",k);
continue;
}
for(int i=1;i<n;i++)
for(int j=0;j<n;j++)
if(i==j+1)
init[i][j]=1;
else init[i][j]=0;
k-=9;
q_mod(k);
int ans=0;
for(int i=0;i<n;i++)
ans=(ans+ret[0][i]*(n-i-1))%mod;
printf("%d\n",ans);
}
return 0;
}
只要知道这个公式,就可以轻松解决了

 View Code
View Code
#include<iostream>
#include<algorithm>
#include<math.h>
using namespace std;
const int N = 2;
int init[N][N],ret[N][N],temp[N][N];
int mod;
void init_(int n)
{
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
ret[i][j]=(i==j);
}
void matmul(int a[][N],int b[][N],int n)
{
memset(temp,0,sizeof(temp));
for(int i=0;i<n;i++)
for(int k=0;k<n;k++)
if(a[i][k])
for(int j=0;j<n;j++)
if(b[k][j])
temp[i][j]=(temp[i][j]+a[i][k]*b[k][j])%mod;
memcpy(a,temp,sizeof(temp));
}
void q_mod(int k,int n)
{
init_(n);
for(;k;k>>=1)
{
if(k&1)
matmul(ret,init,n);
matmul(init,init,n);
}
}
int main()
{
int T,n,m;
scanf("%d",&T);
while(T--)
{
scanf("%d %d",&n,&mod);
if(n==0)
{
printf("0\n");
continue;
}
init[0][0]=init[0][1]=1;
init[1][0]=1;
init[1][1]=0;
q_mod(n*2-1,2);
int ans=ret[0][0]%mod;
printf("%d\n",ans);
}
return 0;
}
分析:
首先,我们将问题整理一下,就是对等差数列 ai=k*i+b,求所有的f(ai)之和除以M的余数
当0<=i<N
大家有没有想到,因为ai是等差数列,倘若f(ai)也是个等什么序列,那说不定就有公式求了
f(ai)显然不是等差数列,直接看上去也不是等比数列
但是如果把f(ai)换成我们刚才所说的Fibonacci矩阵呢?
是的,可是我们对矩阵是直接求幂即可,由于矩阵加法的性质,我们要求A^ai的右上角元素之和,只要求A^ai之和的右上角元素
就矩阵这个东西来说,完全可以看作一个等比数列, 首项是:A^b 公比是:A^k 项数是:N
呵呵,我们可以把问题进一步简化
因为矩阵的加法对乘法也符合分配律,我们提出一个A^b来,形成这样的式子: A^b*( I + A^k + (A^k)^2 + .... + (A^k)^(N-1) )
A^b 和 A^k 显然都可以用我们之前说过的方法计算出来,这剩下一部分累加怎么解决呢
简单起见,设A^k=B 要求 G(N)=I + ... + B^(N-1),设i=N/2 若N为偶数,G(N)=G(i)+G(i)*B^i 若N为奇数,G(N)=I+ G(i)*B + G(i) * (B^(i+1))
呵呵,这个方法就是比赛当时ACRush用的 而农夫用的则是更精妙的方法,大家可想知道
我们来设置这样一个矩阵 B I O I 其中O是零矩阵,I是单位矩阵
将它乘方,得到 B^2 I+B O I 乘三方,得到 B^3 I+B+B^2 O I 乘四方,得到 B^4 I+B+B^2+B^3 O I
既然已经转换成矩阵的幂了,继续用我们的二分或者二进制法,直接求出幂就可以了 该部分解释来自http://www.cnblogs.com/Knuth/archive/2009/09/04/1559951.html
 第二种方法
第二种方法
#include<iostream>
#include<algorithm>
#include<math.h>
using namespace std;
const int N =4;
__int64 init[N][N],temp[N][N],ret[N][N];
__int64 bb[N][N],B[N][N];
int mod;
void init_(int n)
{
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
init[i][j]=1;
init[0][0]=0;
for(int i=0;i<N;i++)
for(int j=0;j<N;j++)
ret[i][j]=(i==j);
}
void matmul(__int64 a[][N],__int64 b[][N],int n)
{
memset(temp,0,sizeof(temp));
for(int i=0;i<n;i++)
for(int k=0;k<n;k++)
if(a[i][k])
for(int j=0;j<n;j++)
if(b[k][j])
temp[i][j]=(temp[i][j]+a[i][k]*b[k][j])%mod;
memcpy(a,temp,sizeof(temp));
}
void q_mod(int n,int k)
{
for(;k;k>>=1)
{
if(k&1)
matmul(ret,init,n);
matmul(init,init,n);
}
}
void make(int n)
{
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
ret[i][j]=(i==j);
memset(init,0,sizeof(init));
for(int i=0;i<n/2;i++)
for(int j=0;j<n/2;j++)
init[i][j]=B[i][j];
for(int i=0;i<n/2;i++)
for(int j=n/2;j<n;j++)
init[i][j]=ret[i][j-n/2];
for(int i=n/2;i<n;i++)
for(int j=n/2;j<n;j++)
init[i][j]=ret[i-n/2][j-n/2];
}
int main()
{
int n,k,b;
while(scanf("%d %d %d %d",&k,&b,&n,&mod)==4)
{
init_(2);
q_mod(2,b);
memcpy(bb,ret,sizeof(ret));
init_(2);
q_mod(2,k);
memcpy(B,ret,sizeof(ret));
make(4);
q_mod(4,n);
for(int i=0;i<2;i++)
for(int j=0;j<2;j++)
ret[i][j]=ret[i][j+2];
matmul(bb,ret,2);
printf("%I64d\n",bb[0][1]%mod);
}
return 0;
}
很有意思的题目,利用图的邻接矩阵和矩阵运算的性质
很裸的题目
 View Code
View Code
#include<iostream>
#include<algorithm>
#include<string>
using namespace std;
const int N = 21;
const int MOD = 1000;
int n,m;
int init[N][N],ret[N][N],temp[N][N];
int g[N][N];
void init_()
{
memcpy(init,g,sizeof(g));
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
ret[i][j]=(i==j);
}
void matmul(int a[][N],int b[][N])
{
memset(temp,0,sizeof(temp));
for(int i=0;i<n;i++)
for(int k=0;k<n;k++)
if(a[i][k])
for(int j=0;j<n;j++)
if(b[k][j])
temp[i][j]=(temp[i][j]+a[i][k]*b[k][j])%MOD;
memcpy(a,temp,sizeof(temp));
}
void q_mod(int k)
{
init_();
for(;k;k>>=1)
{
if(k&1)
matmul(ret,init);
matmul(init,init);
}
}
int main()
{
while(scanf("%d %d",&n,&m)==2 && (n||m))
{
int a,b,t;
memset(g,0,sizeof(g));
for(int i=0;i<m;i++)
{
scanf("%d %d",&a,&b);
g[a][b]=1;
}
scanf("%d",&t);
while(t--)
{
int k;
scanf("%d %d %d",&a,&b,&k);
q_mod(k);
printf("%d\n",ret[a][b]);
}
}
return 0;
}
hdu3306 Another kind of Fibonacci
一开始面对这个平方和束手无策呀,后来将利用递推式将平方展开之后,发现还是一个递推式,而且我们S(n)=S(n-1)+A(n)^2
所以,就可以构造出一个矩阵出来了

 View Code
View Code
#include<iostream>
#include<algorithm>
#include<string>
using namespace std;
const int N = 4;
const __int64 MOD = 10007;
__int64 init[N][N],temp[N][N],ret[N][N];
__int64 x,y;
void init_()
{
memset(init,0,sizeof(init));
init[0][0]=init[0][1]=init[2][1]=1;
init[1][1]=((x%MOD)*x)%MOD;
init[1][2]=((y%MOD)*y)%MOD;
init[1][3]=((2*x)%MOD*y)%MOD;
init[3][1]=x%MOD;
init[3][3]=y%MOD;
for(int i=0;i<N;i++)
for(int j=0;j<N;j++)
ret[i][j]=(i==j);
}
void matmul(__int64 a[][N],__int64 b[][N])
{
memset(temp,0,sizeof(temp));
for(int i=0;i<N;i++)
for(int k=0;k<N;k++)
if(a[i][k])
for(int j=0;j<N;j++)
if(b[k][j])
temp[i][j]=(temp[i][j]+a[i][k]*b[k][j])%MOD;
memcpy(a,temp,sizeof(temp));
}
void q_mod(int k)
{
init_();
for(;k;k>>=1)
{
if(k&1)
matmul(ret,init);
matmul(init,init);
}
}
int main()
{
__int64 n;
while(scanf("%I64d %I64d %I64d",&n,&x,&y)==3)
{
q_mod(n);
__int64 ans=0;
for(int i=0;i<N;i++)
ans=(ans+ret[0][i])%MOD;
printf("%I64d\n",ans);
}
return 0;
}
关键还是求出递推式子,纠结了好久,利用DFA,有限自动机,找出状态之间的转移
这里解释的很详细http://blog.chinaunix.net/uid-24323834-id-261400.html
 View Code
View Code
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 4;
int init[N][N],temp[N][N],ret[N][N];
int mod;
void init_()
{
memset(init,0,sizeof(init));
init[0][0]=init[0][2]=init[0][3]=1;
for(int i=1;i<N;i++)
for(int j=0;j<N;j++)
if(i==j+1)
init[i][j]=1;
for(int i=0;i<N;i++)
for(int j=0;j<N;j++)
ret[i][j]=(i==j);
}
void matmul(int a[][N],int b[][N])
{
memset(temp,0,sizeof(temp));
for(int i=0;i<N;i++)
for(int k=0;k<N;k++)
if(a[i][k])
for(int j=0;j<N;j++)
if(b[k][j])
temp[i][j]=(temp[i][j]+a[i][k]*b[k][j])%mod;
memcpy(a,temp,sizeof(temp));
}
void q_mod(int k)
{
init_();
for(;k;k>>=1)
{
if(k&1)
matmul(ret,init);
matmul(init,init);
}
}
int main()
{
int n;
int f[5]={0,2,4,6,9};
while(scanf("%d %d",&n,&mod)==2)
{
if(n<=4)
{
printf("%d\n",f[n]%mod);
continue;
}
q_mod(n-4);
int ans=0;
for(int i=0;i<4;i++)
ans=(ans+ret[0][i]*f[4-i])%mod;
printf("%d\n",ans);
}
return 0;
}
题意:同样,还是递推式的问题
给你n个硬币,问你存在连续相同(正面or反面)长度>2的排列数。
n很大,显然dp还要加上优化,n<=(10^9),很显然的是用矩阵。
dp[i][j]表示前i个硬币最后j个是连续的。
那么dp[i][j]只有两种转移方法:dp[i+1][j+1],dp[i+1][1];
因为长度一旦超过2,我们就可以确定这个排列是符合要求的,后面的任何一位不管是正面还是反面都满足要求,所以就可以算出dp[i][3]*2^(n-i);
一旦出现了连续三个就可以满足这个式子。
dp[i][3]=dp[i-1][2];
dp[i][2]=dp[i-1][1];
dp[i][1]=dp[i-1][1]+dp[i-1][2];
dp[1][1]=2;dp[1][2]=0;dp[1][3]=0;
这里我们引入多一列dp[i][4]记录前面满足条件的总数;
dp[i][4]=dp[i-1][3]+dp[i-1][4]*2(这里乘2,就是前面满足条件的排列在第i位可以任意放);
 View Code
View Code
#include<iostream>
#include<algorithm>
#include<string>
using namespace std;
const int MOD = 10007;
const int N =4;
int init[N][N],ret[N][N];
void init_()
{
for(int i=0;i<N;i++)
for(int j=0;j<N;j++)
ret[i][j]=(i==j);
memset(init,0,sizeof(init));
init[0][0]=2;
init[0][1]=init[1][2]=init[2][3]=init[3][3]=init[3][2]=1;
}
void matmul(int a[][N],int b[][N])
{
int temp[N][N]={0};
for(int i=0;i<N;i++)
for(int k=0;k<N;k++)
if(a[i][k])
for(int j=0;j<N;j++)
if(b[k][j])
temp[i][j]=(temp[i][j]+a[i][k]*b[k][j])%MOD;
memcpy(a,temp,sizeof(temp));
}
void q_mod(int k)
{
init_();
for(;k;k>>=1)
{
if(k&1)
matmul(ret,init);
matmul(init,init);
}
}
int main()
{
int n;
while(scanf("%d",&n)==1)
{
if(n<=2)
{
printf("%d\n",0);
continue;
}
q_mod(n);
printf("%d\n",(ret[0][3]*2)%MOD);
}
return 0;
}
题意:求出长度为1~n的串中包含K种颜色的珠子的方案数

构造完矩阵之后,之后就是跟hdu1588类似的过程,注意矩阵中的值,哪一个才是想要求的
 View Code
View Code
#include<iostream>
#include<algorithm>
#include<string>
using namespace std;
const int N = 61;
const __int64 MOD = 1234567891;
__int64 init[N][N],ret[N][N],temp[N][N];
void init_(int k)
{
memset(init,0,sizeof(init));
for(int i=0;i<k-1;i++)
{
init[i][i]=k-i;
init[i][i+1]=k-i-1;
}
init[k-1][k-1]=1;
for(int i=0;i<k;i++)
init[i][i+k]=1;
for(int i=k;i<2*k;i++)
init[i][i]=1;
for(int i=0;i<2*k;i++)
for(int j=0;j<2*k;j++)
ret[i][j]=(i==j);
}
void matmul(__int64 a[][N],__int64 b[][N],int n)
{
memset(temp,0,sizeof(temp));
for(int i=0;i<n;i++)
for(int k=0;k<n;k++)
if(a[i][k])
for(int j=0;j<n;j++)
if(b[k][j])
temp[i][j]=(temp[i][j]+a[i][k]*b[k][j])%MOD;
memcpy(a,temp,sizeof(temp));
}
void q_mod(int n,int k)
{
init_(n);
for(;k;k>>=1)
{
if(k&1)
matmul(ret,init,2*n);
matmul(init,init,2*n);
}
}
int main()
{
int T,n,k;
scanf("%d",&T);
while(T--)
{
scanf("%d %d",&n,&k);
q_mod(k,n);
printf("%I64d\n",(ret[0][2*k-1]*k)%MOD);
}
return 0;
}
与3306完全类似,不过要注意最后负数的处理
 View Code
View Code
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 4;
__int64 mod;
__int64 ret[N][N],init[N][N];
void init_(__int64 a2)
{
memset(init,0,sizeof(init));
init[0][0]=init[0][3]=init[1][3]=init[3][1]=1;
init[2][2]=-1;
init[0][1]=init[1][1]=(((4*a2)%mod)*a2)%mod;
init[0][2]=init[1][2]=((-4)*a2)%mod;
init[2][1]=(2*a2)%mod;
for(int i=0;i<N;i++)
for(int j=0;j<N;j++)
ret[i][j]=(i==j);
}
void matmul(__int64 a[][N],__int64 b[][N])
{
__int64 temp[N][N]={0};
for(int i=0;i<N;i++)
for(int k=0;k<N;k++)
if(a[i][k]!=0)
for(int j=0;j<N;j++)
if(b[k][j]!=0)
temp[i][j]=(temp[i][j]+a[i][k]*b[k][j])%mod;
memcpy(a,temp,sizeof(temp));
}
void q_mod(int k,__int64 a2)
{
init_(a2);
for(;k;k>>=1)
{
if(k&1)
matmul(ret,init);
matmul(init,init);
}
}
int main()
{
int T,n;
__int64 v[4],a2;
scanf("%d",&T);
while(T--)
{
scanf("%I64d %d %I64d",&a2,&n,&mod);
if(n==2)
{
printf("%I64d\n",(((a2%mod)*a2)%mod+1)%mod);
continue;
}
v[0]=(((a2%mod)*a2)%mod+1)%mod;
v[1]=((a2%mod)*a2)%mod;
v[2]=a2%mod;
v[3]=1;
q_mod(n-2,a2);
__int64 ans=0;
for(int i=0;i<N;i++)
ans=(ans+ret[0][i]*v[i])%mod;
if(ans<0)
printf("%I64d\n",ans+mod);
else printf("%I64d\n",ans);
}
return 0;
}
同样,利用图的邻接矩阵的性质,不过要先离散化,矩阵不大,可以直接打表
 View Code
View Code
#include<iostream>
#include<algorithm>
#include<string>
#include<map>
using namespace std;
const int MOD =2008;
const int N = 30;
int g[N][N];
int ans[10001][N][N];
map<int,int> ms;
void matmul(int a[N][N],int m,int n)
{
int temp[N][N]={0};
for(int i=0;i<n;i++)
for(int k=0;k<n;k++)
if(a[i][k])
for(int j=0;j<n;j++)
if(g[k][j])
temp[i][j]=(temp[i][j]+a[i][k]*g[k][j])%MOD;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
ans[m][i][j]=temp[i][j];
}
int main()
{
int n,m,t1,t2,u,v;
int v1,v2;
while(scanf("%d",&n)==1)
{
ms.clear();
int num=0;
memset(g,0,sizeof(g));
for(int i=0;i<n;i++)
{
scanf("%d %d",&u,&v);
if(ms.find(u)==ms.end())
ms[u]=num++;
if(ms.find(v)==ms.end())
ms[v]=num++;
g[ms[u]][ms[v]]++;
}
memcpy(ans[0],g,sizeof(g));
for(int i=1;i<=10000;i++)
{
matmul(ans[i-1],i,num);
}
scanf("%d",&m);
while(m--)
{
__int64 ans1=0;
scanf("%d %d %d %d",&v1,&v2,&t1,&t2);
if(ms.find(v1)==ms.end()||ms.find(v2)==ms.end())
{
printf("0\n");
continue;
}
if(t1>t2)
swap(t1,t2);
for(int i=t1==0?t1:t1-1;i<t2;i++)
ans1=(ans1+ans[i][ms[v1]][ms[v2]])%MOD;
printf("%I64d\n",ans1);
}
}
return 0;
}
求递推式的方式跟之前的很类似,不过首先我们要知道,要使用矩阵来实现状态的转移是有条件的,每一个状态之间的转移必须情况是一样的,同时,是在二维的状态上转移,如果直接求的话,我们需要记录的状态有三个,是否为符合要求的串,也就是串中是否有至少一对相邻的字母的ASCii相差32,以什么字母结尾,还有当前的长度,,很明显,这三个状态都是必不可少的,那该怎么办,正难则反,“至少一个”,对立面是什么,我们可以考虑求出相邻字母小于等于32的字符串的方案数和相邻字母相差小于32的字符串的方案数,那么俩者相减即为所有了,这俩种都可以通过构造矩阵求出
 View Code
View Code
#include<iostream>
#include<algorithm>
#include<math.h>
using namespace std;
const int N = 52;
const __int64 MOD = 1000000007;
__int64 ret[N][N],init[N][N];
__int64 A[N][N],B[N][N];
void matmul(__int64 a[][N],__int64 b[][N])
{
__int64 temp[N][N]={0};
for(int i=0;i<N;i++)
for(int k=0;k<N;k++)
if(a[i][k])
for(int j=0;j<N;j++)
if(b[k][j])
temp[i][j]=(temp[i][j]+a[i][k]*b[k][j])%MOD;
memcpy(a,temp,sizeof(temp));
}
void q_mod(int k)
{
for(int i=0;i<N;i++)
for(int j=0;j<N;j++)
ret[i][j]=(i==j);
for(;k;k>>=1)
{
if(k&1)
matmul(ret,init);
matmul(init,init);
}
}
int main()
{
char letter[N];
memset(A,0,sizeof(A));
memset(B,0,sizeof(B));
for (int i = 'a';i <= 'z';i++)
{
letter[i - 'a'] = i;
letter[i - 'a' + 26] = i - 'a' + 'A';
}
for (int i = 0;i < N;i++)
{
for (int j = 0;j < N;j++)
{
if (abs(letter[i] - letter[j]) <= 32) A[i][j] = 1;
if (abs(letter[i] - letter[j]) < 32) B[i][j] = 1;
}
}
int T,n;
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
__int64 ans1=0,ans2=0;
memcpy(init,A,sizeof(A));
q_mod(n-1);
for(int i=0;i<N;i++)
for(int j=0;j<N;j++)
ans1=(ans1+ret[i][j])%MOD;
memcpy(init,B,sizeof(B));
q_mod(n-1);
for(int i=0;i<N;i++)
for(int j=0;j<N;j++)
ans2=(ans2+ret[i][j])%MOD;
printf("%I64d\n",(ans1-ans2+MOD)%MOD);
}
return 0;
}
这题目,我想,如果事先知道是用矩阵做的话,应该不难想出如何构造矩阵了,关键是在不知道用矩阵做的情况下,该怎么去思考 呢?
其实,这类题目有一个共同点,就是递推,或者说是状态的转移,而这个题目就很好的诠释了这一点,当前状态是否改变与前一个状态有关,而且,前后状态的转移方式是一样的

 View Code
View Code
#include<iostream>
#include<algorithm>
#include<math.h>
using namespace std;
const int N = 100;
const int MOD = 2;
int init[N][N],ret[N][N],temp[N][N];
void matmul(int a[][N],int b[][N],int n)
{
memset(temp,0,sizeof(temp));
for(int i=0;i<n;i++)
for(int k=0;k<n;k++)
if(a[i][k])
for(int j=0;j<n;j++)
if(b[k][j])
temp[i][j]=(temp[i][j]+a[i][k]*b[k][j])%MOD;
memcpy(a,temp,sizeof(temp));
}
void q_mod(int n,int k)
{
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
ret[i][j]=(i==j);
memset(init,0,sizeof(init));
for(int i=0;i<n;i++)
init[i][i]=1;
for(int i=1;i<n;i++)
init[i][i-1]=1;
init[n-1][n-2]=init[0][n-1]=1;
for(;k;k>>=1)
{
if(k&1)
matmul(ret,init,n);
matmul(init,init,n);
}
}
int main()
{
int n,k;
char str[N+1],ans[N+1];
while(scanf("%d",&k)==1)
{
scanf("%s",str);
n=strlen(str);
q_mod(n,k);
for(int i=0;i<n;i++)
{
int t=0;
for(int j=0;j<n;j++)
t+=ret[i][j]*(str[j]-'0');
ans[i]=t%MOD+'0';
}
ans[n]='\0';
puts(ans);
}
return 0;
}
hdu 3096 Life Game
周期L的大小为10^9 这么大的话,首先应该想到的就是矩阵了,其实主要也是因为周期的状态值之间的变换是有规律,这种规律性可以转化为递推式,很明显就可以用矩阵来做了
构造一个01矩阵:行表示每一个位置的标号,(i,j)表示 i 位置可以由j位置累加
 View Code
View Code
#include <iostream> #include<vector> #include<algorithm> #include<string> const int N = 100; using namespace std; int buttom; int n,mod; int map[N][N],a[N]; __int64 temp[N][N]; __int64 init[N][N],ret[N][N]; vector<int> g[N]; int dirup[6][2] = {-1,-1, -1,0, 0,-1,0,1, 1,0, 1,1}; int dirmid[6][2] = {-1,-1, -1,0, 0,-1,0,1, 1,-1, 1,0}; int dirdown[6][2] = {-1,0, -1,1, 0,-1,0,1, 1,-1, 1,0}; int input(int n) { int num=0; for (int i = 1; i <= 2*n - 1; i++ ) { int tt = i > n ? 3*n -i - 1 : n + i -1; for (int j = 1 ; j <= tt; j++) { map[i][j]=num;//给每一个位置标号 scanf("%d",&a[num++]); } } for(int i=0;i<num;i++) g[i].clear(); return num; } inline bool isok(int i , int j) { // if(i < 1 || i > 2*n - 1) return false; int tt = i > n ? 3*n -i - 1 : n + i -1; if(j < 1 || j > tt) return false; return true; } void build(int num) { memset(temp,0,sizeof(temp)); for (int i = 1; i <= 2*n - 1; i++ ) { int tt = i > n ? 3*n -i - 1 : n + i -1; for (int j = 1 ; j <= tt; j++) { for (int k = 0 ; k < 6 ; k++) { int i1,j1; if( i < n ) i1 = dirup[k][0] + i , j1 = dirup[k][1] +j; else if(i == n) i1 = dirmid[k][0] + i , j1 = dirmid[k][1] + j; else i1 = dirdown[k][0] + i , j1 = dirdown[k][1] + j; if(isok(i1,j1)) { g[map[i1][j1]].push_back(map[i][j]); } } } } memset(init,0,sizeof(init)); for(int i=0;i<num;i++)//构造初始矩阵 { init[i][i]=1;//要加上自身的值 for(int j=0;j<g[i].size();j++)//标号为i的位置可以由g[i][j]得到 { init[i][g[i][j]]=1; } } } void matmul(__int64 a[][N],__int64 b[][N],int nn) { memset(temp,0,sizeof(temp)); for(int i=0;i<nn;i++) for(int k=0;k<nn;k++) if(a[i][k]) for(int j=0;j<nn;j++) if(b[k][j]) temp[i][j]=(temp[i][j]+a[i][k]*b[k][j])%mod; memcpy(a,temp,sizeof(temp)); } void q_mod(int nn,int k) { for(int i=0;i<nn;i++) for(int j=0;j<nn;j++) ret[i][j]=(i==j); for(;k;k>>=1) { if(k&1) matmul(ret,init,nn); matmul(init,init,nn); } } int main() { int k,cas=0; while(~scanf("%d%d%d",&n,&mod,&k)) { if(!(n||k||mod)) break; int nn=input(n); build(nn); q_mod(nn,k); __int64 ans=0; for(int i=0;i<nn;i++) { __int64 b=0; for(int j=0;j<nn;j++) { b+=ret[i][j]*a[j]; if(b>=mod) b%=mod; } ans+=b;//注意这里不能取模 } printf("Case %d: %I64d\n",++cas,ans); } return 0; }
hdu3483 A Very Simple Problem
题意:计算

不是自己想出来的,,关于二项式系数,一开始没想到,,,
 View Code
View Code
/*求sum(x^k*k^x) k=1~N x^(k+1)*(k+1)^x=x^k*x*(k+1)^x 然后用二项式定理展开(k+1)^x即可 例如当x=4时 | 1x 0 0 0 0 0 | |x^k*k^0| |x^(k+1)*(k+1)^0| | 1x 1x 0 0 0 0 | |x^k*k^1| |x^(k+1)*(k+1)^1| | 1x 2x 1x 0 0 0 |*|x^k*k^2|=|x^(k+1)*(k+1)^2| | 1x 3x 3x 1x 0 0 | |x^k*k^3| |x^(k+1)*(k+1)^3| | 1x 4x 6x 4x 1x 0 | |x^k*k^4| |x^(k+1)*(k+1)^4| | 1x 4x 6x 4x 1x 1x | | S(k) | | S(k+1) | */ #include<iostream> #include<algorithm> using namespace std; const int N = 50+10; __int64 init[N][N],ret[N][N],temp[N][N]; int mod; void init_mat(int x) { memset(init,0,sizeof(init)); for(int i=0;i<x+2;i++) for(int j=0;j<=i;j++) { if(j==0 || j==i) init[i][j]=x; else { if(i!=x+1) init[i][j]=init[i-1][j-1]+init[i-1][j];//利用杨辉三角的性质求二项式系数 else init[i][j]=init[i-1][j]; init[i][j]%=mod; } } init[x+1][x+1]=1; } void matmul(__int64 a[][N],__int64 b[][N],int n) { memset(temp,0,sizeof(temp)); for(int i=0;i<n;i++) for(int k=0;k<n;k++) if(a[i][k]) for(int j=0;j<n;j++) if(b[k][j]) { temp[i][j]=temp[i][j]+a[i][k]*b[k][j]; if(temp[i][j]>=mod) temp[i][j]%=mod; } memcpy(a,temp,sizeof(temp)); } void q_mod(int k,int n) { for(int i=0;i<n;i++) for(int j=0;j<n;j++) ret[i][j]=(i==j); for(;k;k>>=1) { if(k&1) matmul(ret,init,n); matmul(init,init,n); } } int main() { int n,x; while(scanf("%d %d %d",&n,&x,&mod)==3) { if(n<0 && x<0 && mod<0) break; init_mat(x); q_mod(n-1,x+2); __int64 ans=0; for(int i=0;i<x+2;i++) { ans+=ret[x+1][i]*x; if(ans>=mod) ans%=mod; } printf("%I64d\n",ans); } return 0; }
hdu3509 Buge's Fibonacci Number Problem
解决了上一个题目,那这个题目也很好解决了
 View Code
View Code
/* 题意: F[n] = a*F[n-1]+b*F[n-2] 求 Sn = ∑F[i]^k 矩阵乘法 Sn = ∑F[i]^k = F[n]^k + Sn-1 = (aF[n-1]+bF[n-2])^k + Sn-1 二项式定理展开 = C(k,0)F[n-1]^kF[n-2]^0 + + C(k,k)F[n-1]^0F[n-2]^k + Sn-1 * 构造向量 T(n-1) = (F[n-1]^kF[n-2]^0 , , F[n-1]^0F[n-2]^k , Sn-1) 则T(n) = (F[n]^kF[n-1]^0 , , F[n]^0F[n-1]^k , Sn) 现在的问题是如何构造出矩阵A,使得 T(n-1)*A = T(n) 由式子*,我们能知道A的最后一列(第K+1列)是(C(k,0) , , C(k,k),1)T 现在剩下的问题是维护向量剩下的那些项,即F[n-1]^xF[n-2]^(k-x) 同样是用二项式定理展开即可,这里不赘述了 */ #include<algorithm> #include<iostream> #include<math.h> using namespace std; const int N = 50+10; __int64 init[N][N],ret[N][N],temp[N][N],C[N][N]; __int64 mod; __int64 xx[N]; __int64 power(__int64 a,int k) { __int64 res=1; for(;k;k>>=1) { if(k&1) res=(res*a)%mod; a*=a; if(a>=mod) a%=mod; } return res; } void show(__int64 a[N][N],int n) { for(int i=0;i<n;i++) { for(int j=0;j<n;j++) cout<<a[i][j]<< ' '; cout<<endl; } } void init_mat(int x,__int64 a,__int64 b,__int64 f1,__int64 f2) { for(int i=0;i<=x;i++) C[i][i]=C[i][0]=1; for(int i=2;i<=x;i++) for(int j=1;j<i;j++) C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod; memset(init,0,sizeof(init)); for(int i=0;i<x+1;i++) for(int j=0;j<=x-i;j++) init[i][j]=(((C[x-i][j]*power(a,x-i-j))%mod)*power(b,j))%mod; for(int j=0;j<x+1;j++) init[x+1][j]=init[0][j]; init[x+1][x+1]=1; for(int i=0;i<x+1;i++) { xx[i]=power(f2,x-i)*power(f1,i); if(xx[i]>=mod) xx[i]%=mod; } xx[x+1]=power(f1,x)+power(f2,x); if(xx[x+1]>=mod) xx[x+1]%=mod; //show(init,x+2); } void matmul(__int64 a[][N],__int64 b[][N],int n) { memset(temp,0,sizeof(temp)); for(int i=0;i<n;i++) for(int k=0;k<n;k++) if(a[i][k]) for(int j=0;j<n;j++) if(b[k][j]) { temp[i][j]=temp[i][j]+a[i][k]*b[k][j]; if(temp[i][j]>=mod) temp[i][j]%=mod; } memcpy(a,temp,sizeof(temp)); } void q_mod(int k,int n) { for(int i=0;i<n;i++) for(int j=0;j<n;j++) ret[i][j]=(i==j); for(;k;k>>=1) { if(k&1) matmul(ret,init,n); matmul(init,init,n); } } int main() { int n,k; int T; __int64 f1,f2,a,b; scanf("%d",&T); while(T--) { scanf("%I64d %I64d %I64d %I64d %d %d %I64d",&f1,&f2,&a,&b,&k,&n,&mod); if(n==1) { printf("%I64d\n",power(f1,k)); continue; } else if(n==2) { __int64 ans=power(f1,k)+power(f2,k); if(ans>=mod) ans%=mod; printf("%I64d\n",ans); continue; } init_mat(k,a,b,f1,f2); q_mod(n-2,k+2); //show(ret,k+2); __int64 ans=0; for(int i=0;i<k+2;i++) ans=(ans+ret[k+1][i]*xx[i])%mod; printf("%I64d\n",ans); } return 0; }
以上部分图片来自《矩阵乘法题目总结》
