啊!DP!
顾名思义,树形DP就是在树上所做的动态规划。我们一般所做的动态规划多是线性的,线性DP我们可以从前向后或从后向前两种方法,不妨类比一下,在树上我们同样可以有两种方法,从根向树叶或者从树叶向根。从根向树叶传值的题不多见,而从叶向根传送值的题较多,下面我们主要来分析这种题。
分析:
把该题抽象到一颗树中,设i的下属就是他的儿子,则有两种情况:
如果i参加,他的儿子就不能参加。
如果i不参加,他的儿子可参加可不参加。
所以设f[i][1]表示i参加,f[i][0]表示i不参加,则有
f[i][0]+=max(f[j][0],f[j][1]); f[i][1]+=f[j][0]+w[i]; //j是i的儿子
所以
ans=max(f[i][1],f[i][0]) //最大快乐指数
得到基础代码:(很粗略,不过好懂)
#include<cstdio> #include<iostream> using namespace std; const int maxn=6005; int f[maxn][2],n,r[maxn]; int son[maxn][maxn],tot[maxn]; int vis[maxn]; int end; void tree_dp(int x) { for (int i=1;i<=tot[x];i++) { int y=son[x][i]; //哪个儿子 tree_dp(y); //刷新y的快乐指数 f[x][0]+=max(f[y][0],f[y][1]); f[x][1]+=f[y][0]; } } void work() { scanf("%d",&n); for (int i=1;i<=n;i++) scanf("%d",&f[i][1]); //父亲(上司)要去的情况,要加本身的快乐指数 int k,l; for (int i=1;i<=n;i++) { scanf("%d%d",&l,&k); if(l!=0&&k!=0) { son[k][++tot[k]]=l; vis[l]=1; //l是儿子 } } for (int i=1;i<=n;i++) { if(!vis[i]) //找根节点(非儿子) { end=i; break; } } tree_dp(end); printf("%d",max(f[end][0],f[end][1])); } int main() { work(); return 0; }
在这里就要说一下vector了,真的很好用
关于DP有一点很重要——多叉树转二叉树。
树有很多种,二叉树是一种人人喜欢的数据结构,简单而且规则。
但一般来说,树形动规的题目很少出现二叉树,因此将多叉树转成二叉树就是一种必备的手段,方法非常简单,“左儿子,右兄弟” 。
就是将一个节点的第一个儿子放在左儿子的位置,下一个儿子,即左儿子的第一个兄弟,放在左儿子的右儿子位置上,再下一个兄弟接着放在右儿子的右儿子,以此类推。
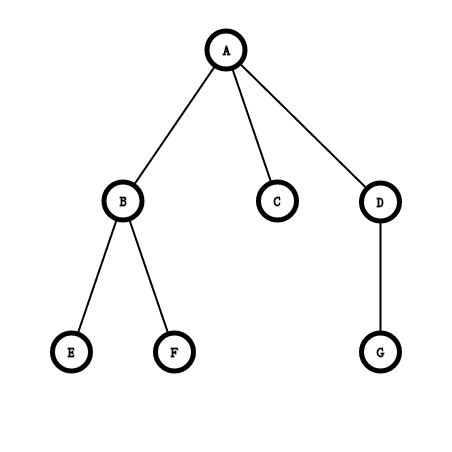 变为
变为
代码:
scanf("%d%d",&u,&v) //v的父亲是u if(l[u]==0) l[u]=v; //多叉树转二叉树 如果u没有儿子,则v作u的儿子 else r[v]=l[u]; //如果u有儿子,则为上一个儿子l[u]的兄弟 l[u]=v; //刷新l[u],作为下一个兄弟的“父亲”
为什么要这样转二叉,等会你就知道了。(好神秘)
分析:以样例为例,课程之间关系如下图:
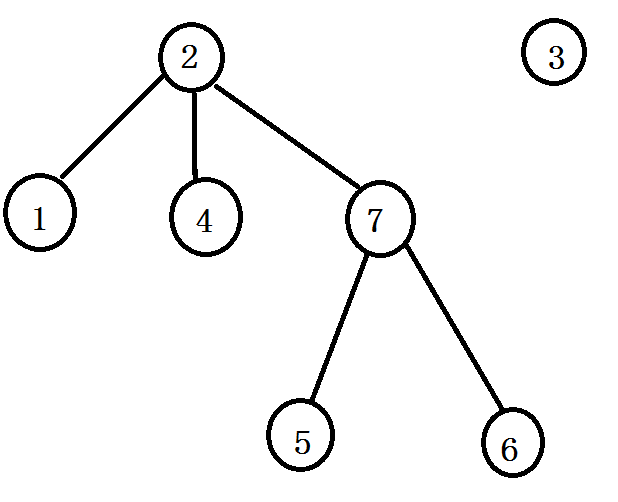 转换为
转换为 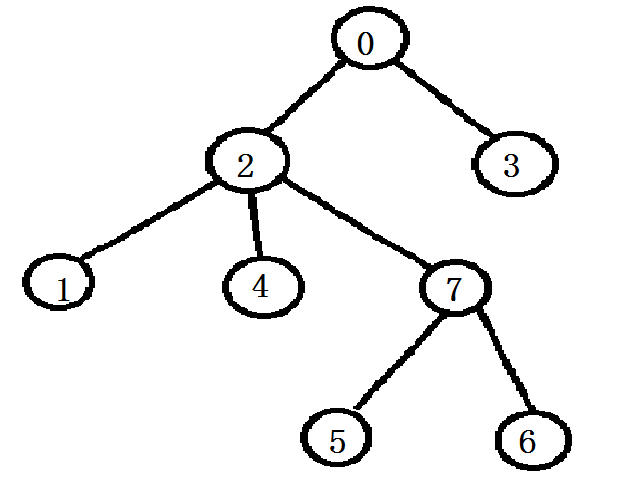
在转化后的二叉树上,我们如果选第1,就必须先选2,如果选3,不一定要选2。
设dp[i][j]表示选到第i门课,还要选j门课的最大学分,那么分两种情况讨论:
如果选i,则还要在l[i]上选k门,并且在r[i]上选就j-k-1门。
如果不选i,则只能在r[i]上选j门,0<=k<j。
现在你知道这种转二叉树的好处了吧。
#include<cstdio> #include<iostream> #include<cstring> using namespace std; const int maxn=305; int n,m; int k,s[maxn]; int last[maxn],l[maxn],r[maxn],vis[maxn][maxn]; int end; int f[maxn][maxn]; int tree_f(int x,int sum) //动归方程 { if(!sum||x==-1) return 0; if(vis[x][sum]!=0) return f[x][sum]; int minn=-1<<30; vis[x][sum]=1; minn=max(minn,tree_f(r[x],sum)); //不选i,就只能在右子树上选sum门。 for (int i=0;i<=sum-1;i++) minn=max(minn,tree_f(l[x],i)+tree_f(r[x],sum-i-1)+s[x]); //选i,左子树上选i门,右子树上选sum-i-1门。 f[x][sum]=minn; return minn; } void work() { memset(l,-1,sizeof(l)); memset(r,-1,sizeof(r)); memset(f,-1,sizeof(f)); scanf("%d%d",&n,&m); for (int i=1;i<=n;i++) { scanf("%d%d",&k,&s[i]); if(l[k]==0) l[k]=i; //多叉树转二叉树 else r[i]=l[k]; l[k]=i; } printf("%d",tree_f(0,m+1)); } int main() { work(); return 0; }
最后再来道题练练手吧(不要害怕,不用多叉树转二叉树)
P2458 [SDOI2006]保安站岗
题目大意:一棵树有N个节点,现在需要将所有节点都看守住,如果我们选择了节点i,那么节点i本身,节点i的父亲和儿子都会被看守住。
每个节点有一个选择代价,求完成任务所需要的最小的代价。
分析:根据每个节点其实有只有三个状态:
①被自己看守;②被儿子看守;③被父亲看守。
我们设这三种状态分别为F1,F2,F3。
当然最终作为答案的根节点没有父亲就没有F3。
接下来我们要考虑怎么转移。
首先看F1,我们规定F1[ i ]代表的是i节点被自己看守且以i为根的子树都已被看守的最小代价,也就是说一定会选择 i 节点自己,答案中必定会加入选择他自己的代价Wi。
因为这个点会被自己看管,所以只要考虑在其儿子的三个状态中选一个最小的,保证这个节点下面的子树都已被看守就行了。
所以F1[ i ] += min( F1[ Si ], F2[ Si ], F3[ Si ] ) + w[ i ],其中Si代表i节点的儿子。
接下来看F2,我们规定F2[ i ]代表i节点被儿子看守且以i为根的子树都已被看守的最小代价,也就是说一定不选i节点,但是至少要在i节点的儿子中选择一个而且最多也就选一个,因为代
价是正数,选一个就能把i看住,就不需要选择多余的点在增加代价了。
因为i节点不能被选,所以只能在其儿子的F1, F2状态中选择小的(F3[ Si ]代表选择i节点,而不能选i节点,所以不能用F3[ Si ]),来保证其子树都已被看守。
所以F2[ i ] += min{ F1[ Si ], F2[ Si ] } + t。t代表选择一个儿子的最小代价:t = F1[ Si ] - min{ F1[ Si ], F2[ Si ] }。
顺便解释一下t的转移:t是Si被看管的代价中选一个最小的,如果是F1,那么说明Si已经被选,就不用再加W[ Si ]了,如果是F2,那么F1 - F2 = W[ i ]。(注意F1和F2代表的意义)
最后看F3,我们规定F3[ i ]代表i节点被父亲看守且以i为根的子树都已经被看守的最小代价,也就是说一定不选i节点和其儿子节点,必须选择他的父亲。因为必须选择父亲,那么i一定会被父亲看守,那么我们只要保证其下面的子树都已被看守,就是在儿子的F1, F2中选一个小的,因为还是不能选i,所以其儿子的F3状态仍然不用考虑,同F2。
所以F3[ i ] += min{ F1[ Si ], F2[ Si ]}。
看代码吧……………*&%^qaq^%&*
#include<cstdio> #include<iostream> #include<cstring> using namespace std; const int maxn=1505; const int inf=0x3f3f3f3f; int n; struct edge{ int num,k,m; }e[maxn]; int s[maxn][maxn],fa[maxn],f1[maxn],f2[maxn],f3[maxn]; int ans; void tree_dp(int i) { f1[i]=e[i].k; f2[i]=f3[i]=0; int minn=inf; for (int j=1;j<=e[i].m;j++) { tree_dp(s[i][j]); f1[i]+=min(f1[s[i][j]],min(f2[s[i][j]],f3[s[i][j]])); f2[i]+=min(f1[s[i][j]],f2[s[i][j]]); int t=f1[s[i][j]]-min(f1[s[i][j]],f2[s[i][j]]); minn=min(minn,t); f3[i]+=min(f1[s[i][j]],f2[s[i][j]]); } f2[i]+=minn; } void work() { scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&e[i].num); //注意读入 scanf("%d%d",&e[e[i].num].k,&e[e[i].num].m); for (int j=1;j<=e[e[i].num].m;j++) { scanf("%d",&s[e[i].num][j]); //儿子节点数 fa[s[e[i].num][j]]=e[i].num; } } memset(f1,inf,sizeof(f1)); memset(f2,inf,sizeof(f2)); memset(f3,inf,sizeof(f3)); for (int i=1;i<=n;i++) { if(!fa[i]) //没有父亲,就是根节点 { tree_dp(i); ans=min(f1[i],f2[i]); //根节点只有2种情况 break; } } printf("%d",ans); } int main() { work(); return 0; }
练习:P2016 战略游戏
总之多练吧%%%%%%ε=ε=ε=┏(゜ロ゜;)┛
提高篇:提升——树形DP