机器学习 Hidden Markov Models 3

Viterbi Algorithm

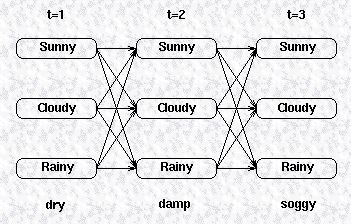
前面我们提到过，HMM的第二类问题是利用HMM模型和可观察序列寻找最有可能生成该观察序列的隐藏变量的序列。简单来说，第一类问题是通过模型计算生成观察序列的概率，而第二类问题通过观察序列计算最有可能生成该观察序列的的隐藏变量的序列。我们还是先来看如下一张图：

这里写图片描述

我们希望找到生成该观察序列的概率最高的一个隐藏变量的序列。换句话说，我们想要最大化如下的式子：

max P r (observed sequence | hidden state combination)

一种简单直观的方法是将所有可能的隐藏变量的序列全部列出，然后求出它们生成可观察序列的概率，然后挑出概率最大的一个隐藏变量序列，这种穷举法无疑是非常低效而且耗时的。与之前介绍的forward算法类似，我们可以借助状态转换矩阵以及confusion矩阵来减低运算的复杂度。

我们还是利用递归的方式去选择这样一条最优的隐藏变量序列，我们先定义一个局部概率Pσ,它表示某一路径到达某一中间状态的概率，这里的局部概率与forward算法里面提到的局部概率有点不一样，forward算法里的局部概率是所有路径到达某一中间状态的概率之和，而这里的局部概率，表示一条最优路径到达某一中间状态的概率。先来看如下的一张图：

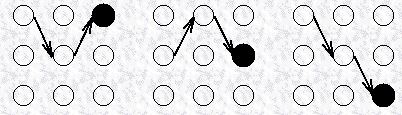
这里写图片描述

对于上图所示的各个路径，无论是到达中间时序的状态，还是到达最终时序的状态，都存在一条最优的路径，比如下图所示分别给出了到达最终时序的三个状态的路径，我们把这些路径称为局部最佳路径，每一个这样的局部最佳路径都有一个概率，称为局部概率，这个定义与forward算法里的局部概率不一样，这里的局部概率表示最佳路径的局部概率。

这里写图片描述

因此，Pσ(i,t)，表示所有在t时刻到达状态i的路径中，最佳的一条局部路径的概率，很显然，对于任何的t,i这样的最佳路径和最大局部概率都是存在的。因此在最终时刻t=T，每一个状态都应该有一个局部最佳路径和最大局部概率，那么全局最佳路径就是选择局部概率最大所对应的那条路径。

对应初始状态的局部概率，其定义和在forward算法中的一样，由初始概率和confusion矩阵决定，如下式所示：

P σ (i, t = 1) = π (i) b i, t = 1

我们接下来将要计算

t时刻的局部概率，同样地利用递归的方法，我们可以通过

t−1时刻的局部概率计算

t时刻的局部概率，我们先看下面的一张图。为了找到在

t时刻到达X状态的最佳路径，我们知道，只有三条路径可以选择，就是从

t−1时刻的状态A,B,C中的一个选择一条最佳路径，

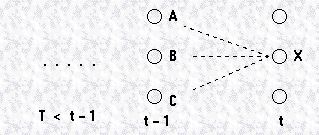
这里写图片描述

之前我们介绍过马尔科夫假设，即一个状态发生的概率只与之前的状态有关，而且对于一阶的马尔科夫过程，当前状态只和前一个状态有关，如果我们要计算状态A到状态X的概率，可以由下式表示：

P r (most probable path to A) \cdot P r (X | A) \cdot P r (observation | X)

因此，

t时刻到达状态X的最佳路径，应该满足如下的表达式：

P r (X t) = max i = A, B, C P r (i t - 1) \times P r (X | i) \times P r (observation | X)

上式右边的第一项是

t−1时刻的局部概率，第二项由状态转换矩阵决定，第三项由confusion矩阵决定。因此，在

t时刻给定观察变量，而推出隐藏变量的状态为

i的概率为：

P σ (i, t) = max j (P σ (j, t - 1) \cdot a j i \cdot b i, t)

现在我们已经知道如何求解到达隐藏变量中间状态和最终状态的局部概率

Pσ(i,t), 但是，我们的目标是通过观察变量的一个序列找到对应的最有可能生成该观察序列的一个隐藏变量序列。

我们已经知道，为了计算时刻t的某一状态的局部概率，我们只要知道t−1时刻的局部概率，一旦计算出局部概率，我们就能确定系统t−1时刻最有可能的状态，我们可以用一个表达式来表示这个选择的过程：

ϕ (i, t) = a r g max j (P σ (j, t - 1) \cdot a j i)

注意到这个表达式和计算局部概率的表达式很像，唯一的区别在于这个表达式没有用到confusion矩阵，也就是没有隐藏变量与观察变量的转换概率。因为这里要找的是隐藏变量的前一个状态，所以与观察变量没有关系。通过这个表达式，我们可以确定到达当前状态i的前一状态j。

下面，我们对这个算法做一个总结，对于有n个隐藏状态的HMM模型，对于每个隐藏状态i,i=1,2,...n，假设存在一组时序长度为T的观察序列：

X i = (X i, 1, X i, 2, . . . X i, T)

隐藏状态的初始局部概率，即

t=1时刻的概率，

Pσ(i,t=1)，可以由转换矩阵和confusion矩阵以及观察序列和隐藏状态的初始概率得到。对于

t=2,3,...T以及

i=1,2,...n。我们有：

P σ (i, t) = max j (P σ (j, t - 1) \cdot a j i \cdot b i, t) ϕ (i, t) = a r g max j (P σ (j, t - 1) \cdot a j i)

假设

i T = a r g max (P σ (i, T))

我们可以知道在

t=T时刻，即最终时刻，哪个状态的局部概率最大。对于

t=T−1,...1，我们有：

i t = ϕ (i t + 1, t + 1)

所以，通过上式进行回溯，一旦回到初始时刻，那么序列

i1,i2,...iT记录的就是最有可能生成观察序列的一个隐藏变量序列。

最后，我们做个小结，对于一个特定的HMM模型，Viterbi Algorithm用来寻找最有可能生成一组观察变量序列的隐藏变量序列，这个算法记录了每一个隐藏状态的局部概率Pσ以及每一个隐藏状态的回溯点ϕ，隐藏状态的局部概率就是通过回溯点到达该状态的概率。

Forward-backward algorithm

前面我们介绍了两类问题，并且介绍了相应的两种算法。第一类问题是用来评估模型的，我们介绍了forward算法；第二类问题是寻找最佳的隐藏变量序列的，我们利用的
是Viterbi算法，这两类问题都要用到已知的模型，转换矩阵，confusion矩阵，观察变量的序列等等。而第三类问题比前两类要复杂地多，它们没有现成的模型，我们需要
估计一个可行的模型，这属于学习问题，这类问题要用Forward-backward算法来解决，这个算法要比前面介绍的两种算法更加复杂，这里就不再详细介绍了。有兴趣的可以
参考下面的文献：

L R Rabiner and B H Juang, `An introduction to HMMs’, IEEE ASSP Magazine, 3, 4-16.

参考来源：

http://www.comp.leeds.ac.uk/roger/HiddenMarkovModels/html_dev/main.html