Support vector machine, SVM
-
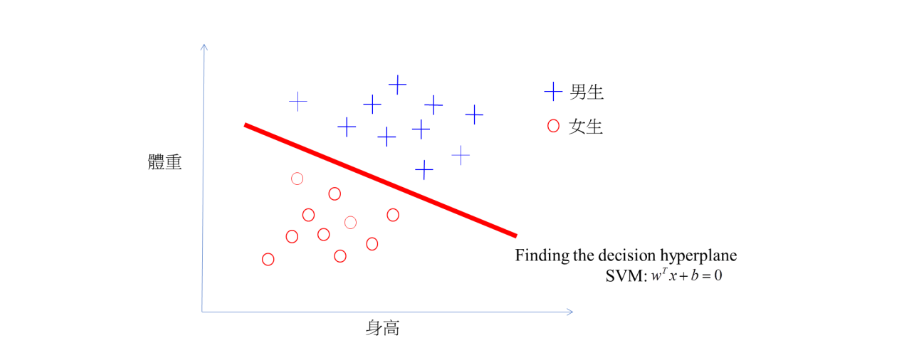
central point is: 找一个决策边界使得两类之间的间隔最大(也就是下图那个红线),间隔最大使它有别于感知机。间隔最大也就一位置以充分大的确信度对它进行分类
-
SVM通过两步来找决策边界:1)将数据映射到一个高维空间里,这时决策边界可以用一个超平面来表示; 2) 尽量让超平面与每个类别最近的数据点之间的距离最大化,从而计算出良好决策边界(分割超平面)
-
涉及到很多向量的内积
source: https://medium.com/@chih.sheng.huang821/機器學習-支撐向量機-support-vector-machine-svm-詳細推導-c320098a3d2e
-
SVM則是去假設有一個hyperplane(wTx+b=0)可以完美分割兩組資料,所以SVM就是在找參數(w和b) 讓兩組之間的距離最大化。
-
svm学习方法包含 线性可分 linearly separable case, 线性支持 以及 非线性支持向量机。
-
当数据线性可分,通过硬间隔最大化 (hard magin maximization) ; 当训练数据近似线性可分,通过 soft margin maximization; 当线性不可分时,用核技巧 kernal trick 及软间隔最大化 学习。
1. 线性可分支持向量机与硬间隔最大化

Form of equation defining the decision surface separating the classes is a hyperplane of the form:
wTx + b = 0
– w is a weight vector
– x is input vector
– b is bias
Functional margin 函数间隔
既然是间隔最大 那首先得了解什么是函数间隔 一般来说 一个点距离分类超平面的远近可以表示分类预测的确信程度

为了约束w,引入了几何间隔 geometric margin, 而根据下面这个图:
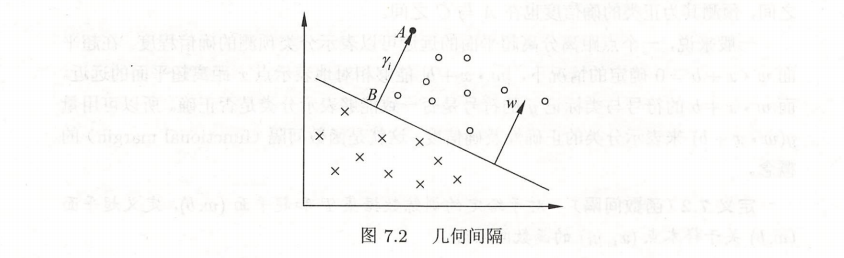
我们可以导出几何间隔的概念:

所以现在基本想法就是能正确划分训练数据集并且集合间隔最大的分离超平面。 而对于这个条件的分离超平面是唯一的。这里的最大化 也是hard margin
这里插一下目标函数 损失函数之类的概念 因为我又搞混了
损失函数(loss function),或者叫代价函数(cost function)。损失函数越小,就代表模型拟合的越好。
这个时候还有一个概念叫风险函数(risk function)。风险函数是损失函数的期望,这是由于我们输入输出的 遵循一个联合分布,但是这个联合分布是未知的,所以无法计算。但是我们是有历史数据的,就是我们的训练集, 关于训练集的平均损失称作经验风险(empirical risk),即 ,所以我们的目标就是最小化 ,称为经验风险最小化。
到这里完了吗?还没有。我们不仅要让经验风险最小化,还要让结构风险最小化。这个时候就定义了一个函数,这个函数专门用来度量模型的复杂度,在机器学习中也叫正则化(regularization)。
到这一步我们就可以说我们最终的优化函数是:即最优化经验风险和结构风险,而这个函数就被称为目标函数。
收
现在得到线性可分支持向量机学习的最优化问题:
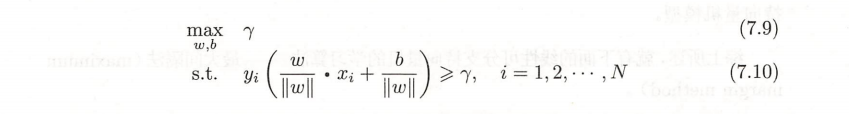
而根据之前得到的几何间隔的概念,又转换成 max λ/||w||的问题。 又函数间隔λ并不影响它的解,故可以去λ = 1, 代入发现最小化 1/||w|| 等价于 最小化的 1/2||w||^2 (想想导数),于是就可以转化为
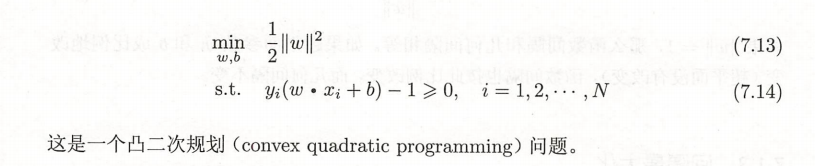
求解这个约束最优化问题得到最优解 w,b,由此得到分离超平面:
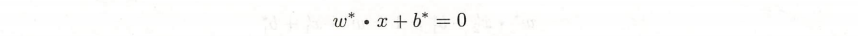
以及分类决策函数:
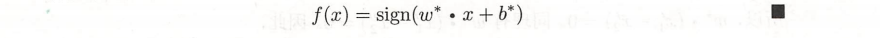
支持向量与间隔边界
训练集的样本点中与分离超平面距离最近的样本点的实例成为 支持向量 support vector,中间有个长带。Example:
source: http://web.mit.edu/6.034/wwwbob/svm-notes-long-08.pdf

分离超平面时只有支持向量起作用,其他实例点不起作用:
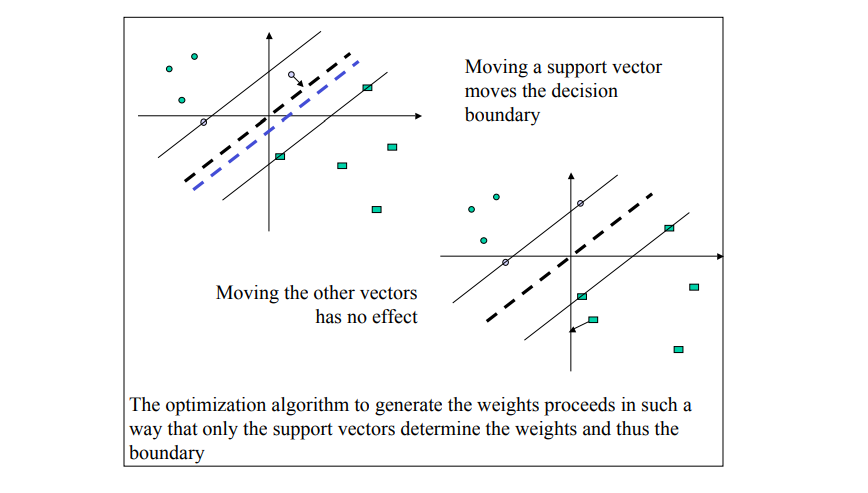
间隔依赖于分离超平面的法向量w, 等于2/||w||
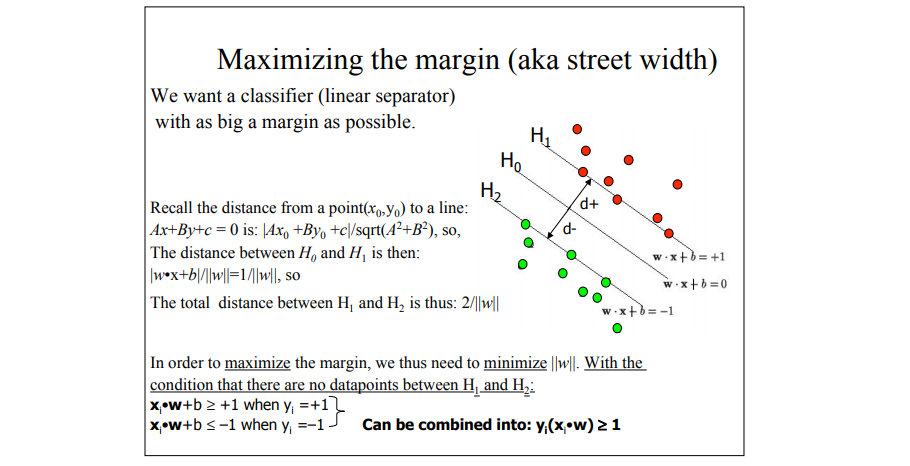
拉格朗日来了
为了求解这个最优化问题,用拉格朗日对偶性,又是上一章的那个dual解决primal的问题。
关于拉格朗日乘子法问题可以参照 https://www.matongxue.com/madocs/939.html 非常清晰 关于 梯度 法向量 约束条件等等
个人理解就是,作为一种约束条件下的最优化求解,也就是求一种最小化距离问题,比如取最小值时两个函数可能相切 (图自Wiki)
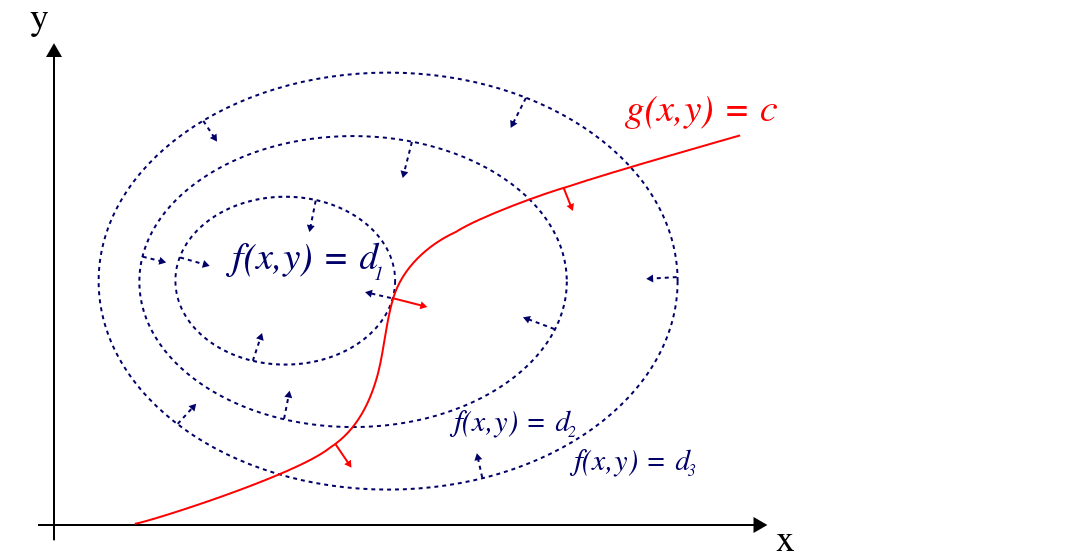
收

整体的学习算法就是:

线性支持向量机和软间隔最大化
- 当线性不可分时... 对每个样本点引入松弛变量,于是原来的目标函数上 加了松弛变量后再支付一个代价
就变成如下凸二次规划问题:
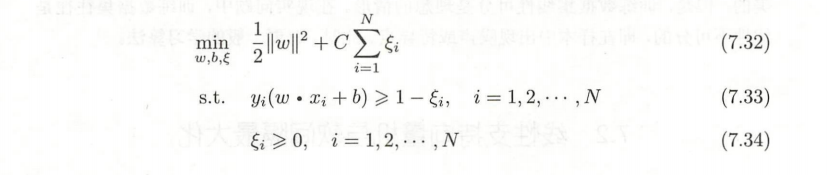
惩罚参数 C > 0
同样为了求出这个问题,对偶问题是拉格朗日函数的极大极小问题。
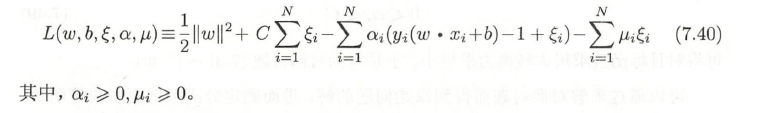
步骤如:
- 先对 w b ξ 求极小,得到三个式子;
- 将得到的式子带入原拉格朗日函数中,在对minL (w, b, ξ, α,μ) 求 α的极大
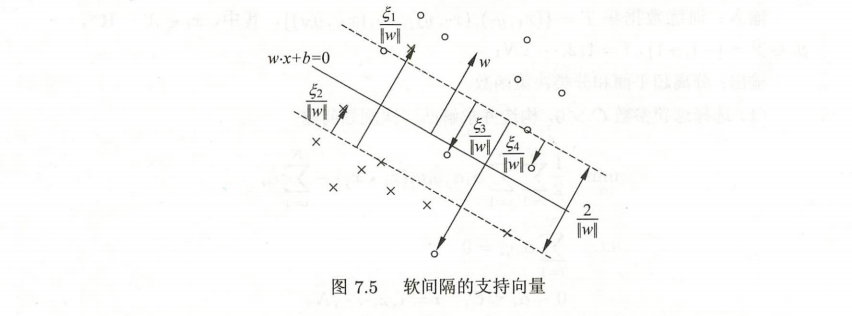
hinge loss function 合页损失函数
线性支持向量机优化目标可写成:
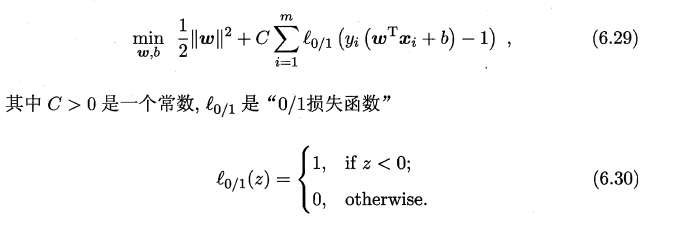
而由于这些l函数非凸 非连续 数学性质不大好 就会使得6.29这个式子不大好解,就会把0-1loss 转换成其他的凸的连续函数且是 l0/1的上届来解,又叫 surrogate loss function
- The penalty for a misclassified point is proportional to the distance from the decision boundary
不同的surrogate loss function对应着不同的优化问题,就有着不同的优化目标和优化方法,也就从本质上定义了不同类型的分类器。 (source:http://sofasofa.io/forum_main_post.php?postid=1000605)
那对于向量机,用的是 hinge loss function , 写法是:

- 一般的 [公式] 是预测值,在-1到1之间, [公式] 是目标值(-1或1)。其含义是, [公式] 的值在-1和+1之间就可以了,并不鼓励 [公式] ,即并不鼓励分类器过度自信,让某个正确分类的样本距离分割线超过1并不会有任何奖励,从而使分类器可以更专注于整体的误差。
- 不仅要分类正确,而且确信度足够高时损失才是0.
3. 非线性支持向量机和核函数
基本想法是 通过一个非线性变换将输入空间对应于一个特征空间 是的在输入控件中的超曲面模型对应于特征空间中的超平面模型。 E.g.

(source: https://towardsdatascience.com/truly-understanding-the-kernel-trick-1aeb11560769)
关于核函数
source:https://github.com/ws13685555932/machine_learning_derivation/blob/master/07 核方法.pdf
Kernel method Kernel trick Kernel function
简而言之就是 非线性带来高维转换 + 对偶表示带来内积
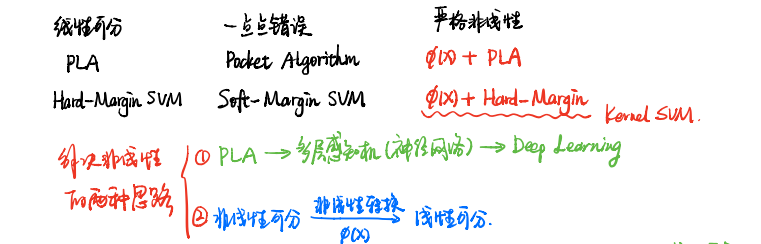
在和函数 K(x,z)给定的条件下,可以利用解线性分类问题的方法求解非线性分类问题的支持向量机
常用核函数
Polynomial Kernel
Gaussian kernel
String kernel
哈哈哈哈哈这个剩下的我都看不懂哈哈哈哈