LCA树上倍增

LCA就是最近公共祖先，比如

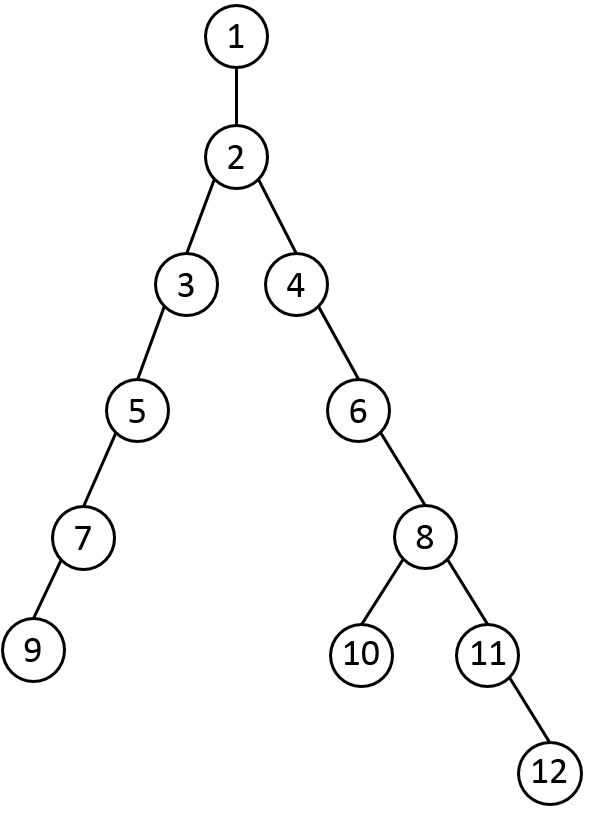
节点10和11的LCA就是8,9和3的LCA就是3。

我们这里讲一下用树上倍增来求LCA。

大家都可以写出暴力解法，两个节点依次一步一步往上爬，直到爬到了相同的一个节点。

二树上倍增就是对暴力的优化，改成了一次爬好几步。

具体怎么爬呢？就是两个点每次爬 2^j 步，而 j 满足的是两个点爬到的点不能相同，因为这样可能是公共祖先，但不一定是最近的。在这种条件下要使 j 尽可能的大。

举个例子，比如上图的节点7和8，当 j = 2 时，都爬到了节点 1，然而很显然这不是 LCA(7, 8)，所以只能取 j = 1,7和8分别跳到3和4。然后发现3和4跳不了了，算法结束，答案就是3和4的父亲节点2。

还有一个小点，若两个点深度不同，只需让深的点往上跳到相同的深度就行。

接下来就开始写代码了。

先要预处理节点 i 跳 2^j 步跳到的点是什么。开一个数组fa[i][j]，代表了节点i向上爬了2^j 步所到达的节点。那么递推式就是 fa[i][j] = fa[fa[i][j - 1]][j - 1]。

然后就直接可以求LCA了。

以洛谷的板子为例。传送门：https://www.luogu.org/problemnew/show/P3379

 1 #include<cstdio>
 2 #include<iostream>
 3 #include<cmath>
 4 #include<algorithm>
 5 #include<cstring>
 6 #include<vector> 
 7 using namespace std;
 8 const int maxn = 5e5 + 5;
 9 vector<int>v[maxn];  
10 int dep[maxn], fa[maxn][25],vis[maxn]; 
11 void dfs(int now)        //预处理 
12 {
13     vis[now] = 1;
14     for(int i = 1; (1 << i) <= dep[now]; ++i)
15         fa[now][i] = fa[fa[now][i - 1]][i - 1];
16     for(int i = 0; i < v[now].size(); ++i)
17         if(!vis[v[now][i]])
18         {
19             dep[v[now][i]] = dep[now] + 1;
20             fa[v[now][i]][0] = now;    //就是v[now][i]的父亲now 
21             dfs(v[now][i]);
22         }
23 }
24 int lca(int x, int y)    //O(logn)
25 { 
26     if(dep[x] < dep[y]) swap(x, y);
27     for(int i = 20; i >= 0; --i)    //使x, y深度相同
28         if(dep[x] - (1 << i) >= dep[y]) x = fa[x][i];
29     if(x == y) return x; //若两点正好重合，直接返回 
30     for(int i = 20; i >= 0; --i)
31         if(fa[x][i] != fa[y][i])
32         {
33             x = fa[x][i]; y = fa[y][i];
34         }
35     return fa[x][0];    //x的父亲节点就是x向上跳2^0步 
36 }
37 int main()
38 {
39     int n, m, s; scanf("%d%d%d", &n, &m, &s);
40     for(int i = 1; i < n; ++i)
41     {
42         int a, b; scanf("%d%d", &a, &b);
43         v[a].push_back(b); v[b].push_back(a);
44     }
45     dfs(s);
46     while(m--)
47     {
48         int a, b; scanf("%d%d", &a, &b);
49         printf("%d
", lca(a, b));
50     }
51     return 0;
52 }

时间复杂度是O(nlogn)。