传送门
IOI的题思维难度确实不小,但是很多题的代码却没有那么难写,也希望这是以后OI以及ACM的出题趋势吧。
首先两个点之间的路径条数不可能等于3,因为如果两点间有3条不同的路径,那么这个图就一定就会有4条路径,见下图:
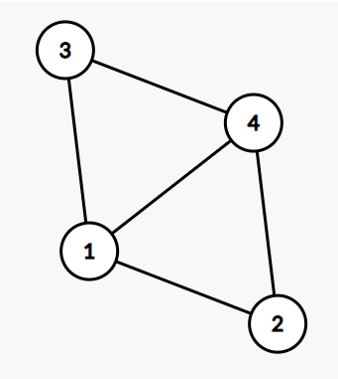
这里能看出1和4之间有3条路径,但2和3之间就有2-1-3,2-1-4-3,2-4-3,2-4-1-3这四条路径。
那么如果(p[i][j] = 3),直接返回0.
现在考虑(p[i][j])为1和2的情况。
对于(p[i][j]=1),就是一棵树;
对于(p[i][j]=2),就是一个环,或者是一个基环树,但是要保证(i)和(j)在环上或者在不同的两棵树上。
那么思路就有了:
1.先判断如果有(p[i][j]=3),直接返回0;
2.否则dfs找到每一个连通块,如果一个连通块内有(p[i][j]=0),也直接返回0;
3.对于(p[i][j]=1)的点,我们要保证(i)和(j)在一棵树里;对于(p[i][j]=2)的点,要保证(i)和(j)在不同的树里。因此用并查集合并所有(p[i][j]=1)的(i)和(j),再判断(p[i][j]=2)的两点是否在一个并查集里,是的话就直接返回0;
4.现在这个连通块一定存在合法的图:我们取每一个并查集的任意一个元素(以代表元为例),将他作为基环树的树根构成环,剩下的点直接以这个点为端点连成一条链即可(因为链也保证了两点间路径条数为1)。这期间还要判断在有(p[i][j]=2)的前提下参与构成环的点是否大于等于3,否则也要返回0.
写起来还是不难的。
//#include "supertrees.h"
#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<vector>
using namespace std;
#define In inline
typedef long long ll;
const int maxn = 1e3 + 5;
void build(std::vector<std::vector<int> > b);
typedef vector<int> Ivec;
vector<Ivec> E;
int n, a[maxn], cnt = 0;
bool vis[maxn];
In void dfs(int now)
{
vis[now] = 1, a[cnt++] = now;
for(int i = 0; i < n; ++i) if(!vis[i] && E[now][i]) dfs(i);
}
int p[maxn];
In int Find(int x) {return x == p[x] ? x : p[x] = Find(p[x]);}
In void merge(int x, int y)
{
int px = Find(x), py = Find(y);
if(px ^ py) p[px] = py;
}
In bool check0()
{
for(int i = 0; i < cnt; ++i)
for(int j = i + 1; j < cnt; ++j) if(!E[a[i]][a[j]]) return 0;
return 1;
}
bool FLG2 = 0;
In bool check2()
{
for(int i = 0; i < cnt; ++i)
for(int j = i + 1; j < cnt; ++j)
if(E[a[i]][a[j]] == 2)
{
FLG2 = 1;
if(Find(a[i]) == Find(a[j])) return 0;
}
return 1;
}
In void divide()
{
for(int i = 0; i < cnt; ++i)
for(int j = i + 1; j < cnt; ++j) if(E[a[i]][a[j]] == 1) merge(a[i], a[j]);
}
int c[maxn], las[maxn], ccnt = 0;
In bool buildGraph(vector<Ivec>& G)
{
ccnt = 0; //get the circle
for(int i = 0; i < cnt; ++i) Find(a[i]);
for(int i = 0; i < cnt; ++i) if(p[a[i]] == a[i]) c[ccnt++] = las[a[i]] = a[i];
if(FLG2 && ccnt < 3) return 0;
if(ccnt > 2)
{
for(int i = 0; i < ccnt - 1; ++i) G[c[i]][c[i + 1]] = G[c[i + 1]][c[i]] = 1;
G[c[0]][c[ccnt - 1]] = G[c[ccnt - 1]][c[0]] = 1;
}
for(int i = 0, x = a[i]; i < cnt; ++i, x = a[i]) //build tree
if(x != p[x])
{
G[x][las[p[x]]] = G[las[p[x]]][x] = 1;
las[p[x]] = x;
}
return 1;
}
int construct(vector<Ivec> e)
{
n = e.size();
for(int i = 0; i < n; ++i)
for(int j = 0; j < n; ++j) if(e[i][j] == 3) return 0;
E = e; vector<Ivec> G(n, Ivec(n));
for(int i = 0; i < n; ++i) p[i] = i;
for(int i = 0; i < n; ++i) if(!vis[i])
{
cnt = 0, dfs(i);
if(!check0()) return 0;
divide(), FLG2 = 0;
if(!check2()) return 0;
if(!buildGraph(G)) return 0;
}
build(G);
return 1;
}