今天来讲讲乘法逆元。
首先是模板题链接
首先,乘法逆元的定义还是简单说一下:
若在mod p意义下,对于一个整数a,有(a imes b≡1(mod p)),那么这个整数d即为a的 乘法逆元,同时a也为d的乘法逆元
然后主要是代码实现。
我们分为两种种情况来求乘法逆元
1.求较少无规律数的乘法逆元
一、扩展欧几里得
已经在扩展欧几里得算法讲过了,这种算法也是较少无规律数算法中较快的一种。
二、费马小定理。
费马小定理:
当(p)为质数时,对于任意整数(a),满足(a^p-a)是(p)的整数倍,在(mod p)意义下可以表示为:
[egin{split}
a^p-a equiv 0pmod{p}\
a^p equiv apmod {p}\
a^{p-1}equiv 1pmod{p}\
a imes a^{p-2}equiv 1pmod{p}
end{split}
]
所以很明显,只需要算出(a^{p-2}mod p)就是(a)在(mod p)意义下的逆元,用快速幂算出来就可以了。
2.求1~n逆元
很明显,这种要求这么多数字的逆元的题目,不能再简单地挨个单个算它的逆元了。
这个时候就需要一种算法,能够在很短的时间内求出这一连串数字在(mod p)意义下的逆元,所以就出现了这种线性算法
它能够用(O(n))的时间复杂度来求出1~n的每一个逆元。
首先 (1^{-1}equiv 1pmod {p})(既然(p)是质数那么(p)一定是(≥2)的整数)
然后设 (p=k*i+r,(1<r<i<p))也就是 (k) 是 (p / i) 的商,(r) 是余数 。
再将这个式子放到(pmod p)意义下就会得到:
(k*i+r equiv 0 pmod p)
然后乘上(i^{-1},r^{-1})就可以得到:
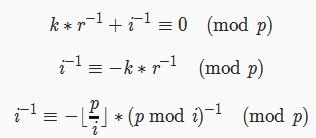
(O(n))递推公式:
inv[i]=(p-p/i)*inv[p%i]%p;
inv[1]初值赋(1).
ov.