题目:

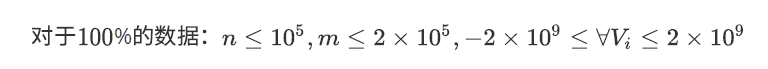
分析:
这道题的正解本来不是倍增,但可以用倍增+卡常莽过去。。。
对于倍增来说,主要思想是将上下两部分信息合并。
一种很直接的想法是:直接带值计算两点间的值。
但这样是错的。
比如说合并a,b的时候:
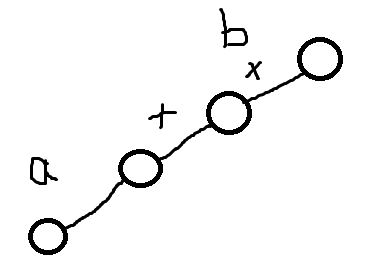
连接他们的是+,但b之前已经执行过一次乘运算了,直接用+合并的话,会变成:a+(c*d),但应该是:(a+c)*d
正确的做法是:对于一个点v,求出它向上的解析式:a*x+b 的形式,x是它自己,要用的时候代入。
然后合并的时候,对于一个解析式:a*x+b,另一个:c*x+d
合在一起,即将前一个视作后一个的x代入,解得新的a=a*c,b=b*c+d
但是这样做保证了是从下往上计算的,而对于一条链来说,还有从上向下计算的情况,就在预处理一个g数组,求的方式与f类似。
询问的时候,两端分别跳倍增,并维护一下左右两边的解析式,最后代入求解即可。
复杂度:O(m*logn)
卡常技巧:
1. 加register int
2. 加 inline
3. 倍增的指数到17(2^17约为1e5)

#include<bits/stdc++.h> using namespace std; #define ll long long #define ri register int #define I inline #define N 200005 const ll mod = 19491001; int to[N],nex[N],head[N],w[N],fa[N][18],dep[N],tot=0; ll ww[N]; struct node { ll a,b; }f[N][18],g[N][18]; I int read() { int x=0,fl=1; char ch=getchar(); while(ch<'0' || ch>'9') { if(ch=='-') fl=-1; ch=getchar(); } while(ch<='9' && ch>='0') x=x*10+ch-'0',ch=getchar(); return x*fl; } I void add(int a,int b,int c) { to[++tot]=b; nex[tot]=head[a]; head[a]=tot; w[tot]=c; } I void dfs(int u,int ff) { for(ri i=head[u];i;i=nex[i]){ int v=to[i]; if(v==ff) continue; fa[v][0]=u; dep[v]=dep[u]+1; for(ri j=1;j<=17;++j) fa[v][j]=fa[fa[v][j-1]][j-1]; f[v][0].a=1; g[v][0].a=1;//记得赋初值 if(w[i]==1) f[v][0].b=ww[u], g[v][0].b=ww[v]; if(w[i]==2) f[v][0].b=-ww[u],g[v][0].b=-ww[v]; if(w[i]==3) f[v][0].a=ww[u], g[v][0].a=ww[v]; for(ri j=1;j<=17;++j){ int tp=fa[v][j-1]; f[v][j].a = f[v][j-1].a * f[tp][j-1].a %mod;//跳倍增的时候根据求出来的式子代入 f[v][j].b =( f[v][j-1].b * f[tp][j-1].a %mod + f[tp][j-1].b ) %mod; g[v][j].a = g[v][j-1].a * g[tp][j-1].a %mod; g[v][j].b =( g[v][j-1].a * g[tp][j-1].b %mod + g[v][j-1].b ) %mod; } dfs(v,u); } } I int lca(int a,int b) { if(dep[a]<dep[b]) swap(a,b); for(ri i=17;i>=0;--i) if(dep[fa[a][i]]>=dep[b]) a=fa[a][i]; if(a==b) return a; for(ri i=17;i>=0;--i) if(fa[a][i]!=fa[b][i]) a=fa[a][i],b=fa[b][i]; return fa[a][0]; } I ll solve(int a,int b,int lc) { ll la=1,lb=0,A=a;//记得记录一下a,否则后面要用的时候会变 for(ri i=17;i>=0;--i)//for到17可卡常 if(dep[fa[a][i]]>=dep[lc]){//求左边的解析式 ll aa=f[a][i].a,bb=f[a][i].b; lb=lb*aa+bb %mod; lb=(lb+mod)%mod; la*=aa; la%=mod; a=fa[a][i]; } ll ra=1,rb=0; for(ri i=17;i>=0;--i) if(dep[fa[b][i]]>=dep[lc]){//求右边的解析式 ll aa=g[b][i].a,bb=g[b][i].b; rb+=bb*ra %mod; rb=(rb+mod)%mod; ra*=aa; ra%=mod; b=fa[b][i]; } ll ans=( ww[A]*la %mod + lb +mod ) %mod;//带值合并 ans=( ans*ra %mod +rb +mod ) %mod; return (ans%mod+mod)%mod; } int main() { freopen("tree.in","r",stdin); freopen("tree.out","w",stdout); int n=read(), m=read(),a,b,c; for(ri i=1;i<=n;++i) ww[i]=read(); for(ri i=1;i<=n-1;++i) a=read(),b=read(),c=read(),add(a,b,c),add(b,a,c); dep[1]=1; dfs(1,0); while(m--){ a=read(); b=read(); int lc=lca(a,b); printf("%lld ",solve(a,b,lc)); } return 0; } /* 5 3 1 3 4 5 6 1 2 3 1 3 1 2 4 2 2 5 3 4 5 5 3 3 5 6 3 3 6 5 7 9 8 1 2 3 1 3 2 3 5 3 5 6 1 2 4 1 6 4 */
