Day 1
上午——基础算法
枚举
例1
求长度为(n)的全排列
题解:
(next\_ permutation)
可你真的知道它的内部实现吗?
实现:
对于当前的一个排列,从后向前找到第一个非增的元素,再从后向前找第一个比它大的元素,交换这两个数,再将后缀翻转。

例2
题解
直接二维前缀和处理,处理完之后枚举
例3
这个题还是蛮有意思的
题解
因为最多只有十颗钻石,地图也十分小,所以我们可以很愉快的暴力
首先,我们预处理出每颗钻石之间的距离,还有每颗钻石到墙壁的最短距离
然后我们对收集钻石的顺序进行全排列枚举,对于每颗钻石,贪心的取它是和上一颗钻石相连还是和墙壁相连
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#define LL long long
using namespace std;
LL read() {
int k = 0, f = 1; char c = getchar();
while(c < '0' || c > '9') {
if(c == '-') f = -1;
c = getchar();
}
while(c >= '0' && c <= '9')
k = k*10+c-48, c=getchar();
return k*f;
}
bool mapp[21][21];
int dis[21][21], len[21], a[21];
struct zzz {
int x, y;
}dia[21]; int tot;
void solve() {
int n = read(), m = read();
memset(mapp, 0, sizeof(mapp)); tot = 0;
memset(dis, 127, sizeof(dis)), memset(len, 127, sizeof(len));
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= m; ++j){
char c; cin >> c;
if(c == '#') mapp[i][j] = 1;
if(c == '*')
dia[++tot].x = i, dia[tot].y = j;
}
for(int i = 1; i <= n; ++i) //到墙壁的最短距离
for(int j = 1; j <= m; ++j)
for(int k = 1; k <= tot; ++k)
if(mapp[i][j])
len[k] = min(len[k], abs(i-dia[k].x)+abs(j-dia[k].y));
for(int i = 1; i <= tot; ++i) //钻石间的最短距离
for(int j = 1; j <= tot; ++j)
dis[i][j] = abs(dia[i].x-dia[j].x)+abs(dia[i].y-dia[j].y);
for(int i = 1; i <= tot; ++i) a[i] = i;
int minn = 0x7fffffff;
while(next_permutation(a+1, a+tot+1)) { //枚举全排列
int ans = 0;
for(int i = 1; i <= tot; ++i)
ans += min(dis[a[i]][a[i-1]], len[a[i]]); //贪心
minn = min(ans, minn);
}
cout << minn << endl;
}
int main() {
int t = read();
while(t--) solve();
return 0;
}
枚举技巧
- 充分利用题目所给出的条件,尽量减少需要枚举的状态
- break 优化:当已经得到答案时,终止循环
- 卡时:在将要超时的情况下停止枚举,直接输出答案
while ((double)clock() / CLOCKS_PER_SEC < 1) work();
搜索
搜索主要讲了各种搜索的概念和实现方法(包括迭代加深/(A^*/IDA^*))
例1
题解
(IDA^*)
估价函数为当前不在指定位置的骑士数
(这题是很久之前做的,可能码风和现在有些不符)
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
int mapp[6][6];
int pd[6][6]={{},
{0,1,1,1,1,1},
{0,0,1,1,1,1},
{0,0,0,-1,1,1},
{0,0,0,0,0,1},
{0,0,0,0,0,0}};
int fx[9]={0,-2,-1,1,2,2,1,-1,-2};
int fy[9]={0,1,2,2,1,-1,-2,-2,-1};
int IDA()
{
int tot=0;
for(int i=1;i<=5;i++)
for(int j=1;j<=5;j++)
{
if(mapp[i][j]!=pd[i][j])
tot++;
}
return tot;
}
bool flag;
void dfs(int x,int y,int deep,int maxd)
{
int step=IDA();
if(step==0)
{
cout<<deep<<endl;
flag=1;
return ;
}
if(deep+step-1>maxd)
return ;
for(int i=1;i<=8;i++)
{
int xx=x+fx[i],yy=y+fy[i];
if(xx>5||xx<1||yy>5||yy<1)
continue;
swap(mapp[x][y],mapp[xx][yy]);
dfs(xx,yy,deep+1,maxd);
if(flag)
return ;
swap(mapp[x][y],mapp[xx][yy]);
}
}
int main()
{
int t; cin>>t;
while(t--)
{
flag=0; int sx,sy;
for(int i=1;i<=5;i++)
for(int j=1;j<=5;j++)
{
char x; cin>>x;
if(x=='*')
{
sx=i,sy=j;
mapp[i][j]=-1;
continue;
}
mapp[i][j]=x-48;
}
for(int i=1;i<=15;i++)
if(!flag) dfs(sx,sy,0,i);
if(!flag) cout<<-1<<endl;
}
return 0;
}
例2
题解
还是(IDA^*)
估价函数为相邻两数的绝对值大于(1)的位置个数
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#define LL long long
using namespace std;
LL read() {
int k = 0, f = 1; char c = getchar();
while(c < '0' || c > '9') {
if(c == '-') f = -1;
c = getchar();
}
while(c >= '0' && c <= '9')
k = k*10+c-48, c=getchar();
return k*f;
}
int a[31], n, maxd;
inline int IDA() {
int cnt = 0;
for(int i = 2; i <= n; ++i)
cnt += (abs(a[i] - a[i-1]) > 1);
return cnt;
}
bool dfs(int deth, int pre) {
if(deth == maxd) {
for(int i = 1; i <= n-1; ++i)
if(a[i] > a[i+1]) return 0;
return 1;
}
if(deth + IDA() > maxd) return 0;
for(int i = 2; i <= n; ++i) {
if(i == pre) continue;
reverse(a+1, a+i+1);
if(dfs(deth + 1, i)) return 1;
else reverse(a+1, a+i+1);
}
return 0;
}
void solve() {
n = read(), maxd = 0;
for(int i = 1; i <= n; ++i) a[i] = read();
for(maxd = 0; maxd <= 30; ++maxd)
if(dfs(0, 0)){
printf("%d
", maxd);
break;
}
}
int main() {
int t = read();
while(t--) solve();
return 0;
}
分治
分治是老师讲课的重点,也是这些“基础算法”中我最不擅长的
例1
给定一个数列(a_1,a_2,...,a_n)和两个参数(q_l,q_r)。求出满足(q_l < a_x+a_y < qr(x < y))的点对((x,y))的个数。(n ≤ 5×10^5,0 ≤ q_l,q_r,|a_i|≤ 10^9)
题解
这道题分治还是比较容易想的。
递归处理([l,mid],(mid,r)),合并的时候用归并排序排序,再利用单调性,用双指针维护答案
例2
很经典的一道题目,之前也在校内模拟赛中见过,然而现在还不是很会
题解
对于当前处理的这个区间,我们可以找出这个区间的最小值和最大值。设最小值位置为(q),最大值位置为(p)
因为只包含最小值是不可能成为答案的,所以我们用(a_q imes a_p)去更新区间(|p-q|) ~ (r-l)
如果我们从中间分开,要讨论的情况比较多。
注意数据随机这一条件,因为数据随机,我们不需要从中间分治也可以使时间复杂度为(O(n log n))
所以我们可以考虑从最小值处分治
接着递归([l,q))和([q + 1,r))
最后,我们发现随着长度的递减, 答案是单调递增的,所以每次只需要更新长度为(r−l)的答案,做一个后缀最大值即可
例3
定义一个数列是合法的,当且仅当这个数列的每一个子串都至少存 在一个只出现过一次的元素。给定一个序列(a_1,a_2,...,a_n),判断这个序列是否合法(n leq 2 imes 10^5)
题解
老师说线段树做法很显然,可我不会啊。
然后老师讲了分治的做法
首先预处理出(pre(i))和(next(i)),分别表示与(a_i)值相同的上一个位置和下一个位置。然后我们就能知道(a_i)是否在([l,r])中只出现了一次。
设在这个区间只出现了一次的数的位置为(p),显然,我们要递归([l,p))和([p + 1,r))。
但这道题的数据并不随机,我们这么递归很可能会使时间复杂度退化成(O(n^2))。
我们可以这样分治:从左右端点同时开始找 只出现一次的数(只出现一次的数在大部分情况下不止一个),只要找到一个就进行递归
这么分治,时间复杂度为(O(n log n))
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <map>
#define LL long long
using namespace std;
int read() {
int k = 0, f = 1; char c = getchar();
while(c < '0' || c > '9') {
if(c == '-') f = -1;
c = getchar();
}
while(c >= '0' && c <= '9')
k = k * 10 + c - 48, c = getchar();
return k * f;
}
map <int, int> q;
int a[200010], pre[200010], suf[200010];
bool solve(int l, int r) {
if(l == r) return 1;
int L = l, R = r;
while(L <= R) {
if(pre[L] < l && suf[L] > r) {
return solve(l, L) && solve(L+1, r);
break;
}
if(pre[R] < l && suf[R] > r) {
return solve(l, R-1) && solve(R, r);
break;
}
++L, --R;
}
return 0;
}
int main() {
int t = read();
while(t--) {
int n = read(); q.clear();
for(int i = 1; i <= n; ++i) {
a[i] = read();
if(!q[a[i]]) q[a[i]] = i, pre[i] = 0;
else pre[i] = q[a[i]], q[a[i]] = i;
}
q.clear();
for(int i = n; i >= 1; --i) {
if(!q[a[i]]) q[a[i]] = i, suf[i] = n+1;
else suf[i] = q[a[i]], q[a[i]] = i;
}
if(solve(1, n)) printf("non-boring
");
else printf("boring
");
}
return 0;
}
下午——考试
考的非常不好(虽然是普遍不好,满分(300),(rank1)才(110pts)),但还是有些自身原因
因为牵扯到版权问题,就不把题目放出来了
Day 2
上午——数论
说句实话,我最不擅长的两样东西,一是(DP),二是数论……
全程掉线……我有什么办法啊!我也很绝望啊!
基础知识还好,一讲例题就见神仙啊!满屏的数学推导真的大丈夫?
好吧,菜是原罪……
不想整理,因为不会,整理也是自欺欺人,把老师讲的例题放在这吧
- Bzoj 4833 [Lydsy1704月赛]最小公倍佩尔数
- HDU 5780 gcd
- Bzoj 3884 上帝与集合的正确用法
- Bzoj 1129 [POI2008]Per
- Bzoj 2159 Crash 的文明世界
下午——数据结构
数据结构还好一些
堆
例1
给出一支股票,它在第(i)天的价格为(a_i)。每一天你可以花费(a_i)买 入一股或者卖出一股得到(a_i)的收益,可以什么都不做。求最大收益。
(n ≤ 10^5)
题解
用堆来贪心
到第(i)天,如果(a_i < top)(top是堆顶),那么(ans + a_i - top),弹出堆顶。
相当于在之前价格为堆顶时买入,第(i)天卖出
接下来是最关键的一步:(a_i)要入堆两次
为什么要入堆两次呢?
这是为了有一个“后悔”操作
如果只入堆一次,有可能会出现这种情况
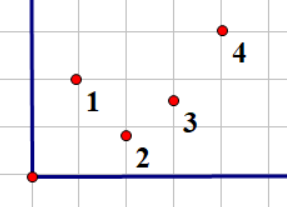
如果只入堆一次,(2,3)匹配,(3,4)匹配,(3)被用了两次,显然不合法
如果不入堆,那么(2,3)匹配,(1,4)匹配
而最优的方案显然是(2,4)匹配
如果我们将(3)入堆两次,就不会出现以上情况
例2
给出一支股票,它在第(i) 天的价格为(a_i) 。每一天你可以花费(a_i)买
入一股或者卖出一股得到(a_i )的收益,每天必须进行买卖。
求最大收益。
例1的变式,变得复杂了些。
题解
同样用一个小根堆维护所有已经卖出的节点。
我们每天的决策分为以下几步:
- 如果当前有一个之前买入的、未被匹配的点,卖出当前点,并将当前点加入堆以供未来的某一天抢走这个匹配。
- 如果当前不存在任何可以抢走匹配的点(或是还没有买任何点),只能买入。
- 如果堆顶大于当前股票价格,抢走堆中的匹配不能让答案变优,于是买入。
- 如果堆顶小于当前股票价格,就抢走当前堆顶的点的匹配(把堆顶变成买入,把新的卖出点加入堆),并记录接下来的某一天可以卖出一次(因为堆顶变成了买入)
老师的示例代码
for (int i = 1; i <= N; ++i) {
int t;
scanf("%d", &t);
if (now >= 1) { // 如果现在还有一个可以买入的点,立刻卖出
result += t;
q.push(t), now--;
} else {
if (q.empty()) // 当前点不存在一个可以抢走匹配的点,只能买入
result -= t, ++now;
else {
int x = q.top();
if (x >= t) // 买入更优
result -= t, ++now;
else { // 抢走堆顶的点的匹配
q.pop();
result -= 2 * x;
result += t;
q.push(t), ++now;
}
}
}
}
并查集
例题
给出一个(n × n)的网格,每次删除其中的一条边,并且询问这条边被删除后它的两个端点是否连通(每次询问不独立)。强制在线。
题解
如果不强制在线的话,我们可以正难则反,把删边变成倒着加边
但是这道题强制在线。
所以就有了一个神仙做法:
建出对偶图,每删除一条边,就把相邻的两个格子并入一个集合。如果删除某条边后发现两个格子已经在一个集合内了,说明删除的边构成了一个闭合图形,两个点不连通。
用并查集维护即可
Day 3
上午+下午——数据结构
树状数组
例1
题解
一个数的移动并不会影响比它大的数,所以我们从小到大移动数,贪心的将它移动到比它大的数较少的一边
所以每个数对答案的贡献为(min()左侧比它大的点,右侧比它大的点())
也就是求逆序对,用树状数组即可
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define LL long long
#define lb() (x&-x);
using namespace std;
int read() {
int k = 0, f = 1; char c = getchar();
while(c < '0' || c > '9'){
if(c == '-') f = -1;
c = getchar();
}
while(c >= '0' && c <= '9')
k = k*10+c-48, c=getchar();
return k*f;
}
int tree[300010<<1], n;
void add(int x, int k) {
while(x <= n)
tree[x] += k, x += lb();
}
int sum(int x) {
int ans = 0;
while(x)
ans += tree[x], x -= lb();
return ans;
}
struct zzz{
int a, pos;
}a[300010];
bool cmp(zzz x, zzz y) {
return x.a > y.a;
}
int main() {
//freopen("4240.in", "r", stdin);
//freopen("4240.out", "w", stdout);
n = read();
for(int i = 1; i <= n; ++i) a[i].a = read(), a[i].pos = i;
sort(a+1, a+n+1, cmp);
LL ans = 0; int tot = 1;
for(int i = 1; i <= n;) {
int j = i - 1;
do{
++j;
int x = sum(a[j].pos);
ans += min(x, i-1-x);
}while(a[j].a == a[j+1].a);
for( ; i <= j; ++i) add(a[i].pos,1);
}
printf("%lld", ans);
return 0;
}
例2
题解
二维树状数组
因为权值(1 leq c leq 100),所以我们对于每个权值,都开一个二维树状数组维护(有点暴力)
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define lb(x) (x&-x)
using namespace std;
int read() {
int k = 0, f = 1; char c = getchar();
while(c < '0' || c > '9'){
if(c == '-') f = -1;
c = getchar();
}
while(c >= '0' && c <= '9')
k = k*10+c-48, c=getchar();
return k*f;
}
int n, m;
struct zzz {
int tree[310][310];
void add(int x, int y, int k) {
for(int i = x; i <= n; i += lb(i))
for(int j = y; j <=m; j += lb(j))
tree[i][j] += k;
}
int sum(int x, int y) {
int ans = 0;
for(int i = x; i; i -= lb(i))
for(int j = y; j; j -= lb(j))
ans += tree[i][j];
return ans;
}
}tree[110];
int mapp[310][310];
int main() {
n = read(), m = read();
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= n; ++j) {
int x = read();
mapp[i][j] = x;
tree[x].add(i, j, 1);
}
int q = read();
for(int i = 1; i <= q; ++i) {
int val = read();
if(val == 1) {
int x = read(), y = read(), c = read();
tree[mapp[x][y]].add(x, y, -1);
tree[c].add(x, y, 1);
mapp[x][y] = c;
}
else {
int x1 = read(), x2 = read(), y1 = read(), y2 = read(), c = read();
printf("%d
", tree[c].sum(x2, y2)-tree[c].sum(x1-1, y2)-tree[c].sum(x2, y1-1)+tree[c].sum(x1-1, y1-1));
}
}
return 0;
}
线段树
例1
题目大意:
给出两个排列(a,b),长度分别为 (n,m),你需要计算有多少个(x), 使得 (a_1 + x,a_2 + x,...a_n + x) 是 (b) 的子序列
(n leq m leq 2 imes 10^5)
题解
因为我们要比较区间,先将(a)排列 hash
注意,因为(a)是一个排列,所以它里面的元素一定是从(1)~(n)的,所以,我们可以使pos[b[i]] = i,然后判断pos[i-n+1]~pos[i]和(a)排列是否符合要求
这里的符合要求包括:
pos[i-n+1]~pos[i]减去(x)等于(a)排列b[pos[i-n+1]]~b[pos[i]]是(b)的子序列
而这两个要求都可以通过计算b[pos[i-n+1]]~b[pos[i]]在原排列里构成的子序列的hash值来判断
之后我们要做的就是快速的求出b[pos[i-n+1]]~b[pos[i]]在原排列(b)中构成的子序列的hash值
因为(b_i)并不连续,用线段树维护hash值
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ULL unsigned long long
#define ls (p << 1)
#define rs (p << 1 | 1)
#define mid ((l + r) >> 1)
using namespace std;
int read() {
int k = 0, f = 1; char c = getchar();
while(c < '0' || c > '9'){
if(c == '-') f = -1;
c = getchar();
}
while(c >= '0' && c <= '9')
k = k * 10 + c - 48, c = getchar();
return k * f;
}
int a[200010], b[200010], pos[200010], ans;
ULL hasha, qpow[200010] = {1}, sum;
struct zzz{
ULL a, tot;
}tree[200010 << 2];
void up(int l, int r, int p) {
tree[p].tot = tree[ls].tot + tree[rs].tot;
tree[p].a = tree[ls].a * qpow[tree[rs].tot] + tree[rs].a;
}
void update(int l, int r, int pos, int p, int k) {
if(l == r) {
if(!k) tree[p].tot -= 1;
else tree[p].tot += 1;
tree[p].a = k; return ;
}
if(pos <= mid) update(l, mid, pos, ls, k);
if(pos > mid) update(mid+1, r, pos, rs, k);
up(l, r, p);
}
int main() {
int n = read(), m =read();
for(int i = 1; i <= n; ++i) {
a[i] = read(), hasha = hasha * 23 + a[i];
qpow[i] = qpow[i-1] * 23;
sum += qpow[i-1];
}
for(int i = 1; i <= m; ++i) b[i] = read(), pos[b[i]] = i;
for(int i = 1; i <= m; ++i) {
if(i > n) update(1, m, pos[i-n], 1, 0);
update(1, m, pos[i], 1, i);
int d = i - n;
if(d >= 0 && tree[1].a == d*sum+hasha) ++ans;
}
printf("%d", ans);
return 0;
}
例2
先将楼房高度转化为斜率,这样只用比较斜率大小就能知道我们是否能看到楼房
肯定要用线段树来维护
因为是单点修改,所以我们只考虑怎么合并就好了
只有左边的点对右边的点产生影响,我们可以将左右儿子的最大值(max_l)和(max_r)记录下来
设右儿子的左儿子为(x),右儿子的右儿子为(y)
- (max_l geq max_x),(x)中肯定没有可见的楼房,我们接着递归(y)
- (max_l < max_x),则(y)中可见的楼房均可见,我们接着递归(x)
合并两个子树的复杂度为(O(log n)) ,一次修改的复杂度为 (O(log^2 n)) ,一次查询的复杂度为(O(1))
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#define mid ((l + r) >> 1)
#define LL long long
#define ls p << 1
#define rs p << 1 | 1
using namespace std;
struct zzz {
int ans, l, r;
double maxx;
}tree[100010<<2];
void build(int l, int r, int p) {
tree[p].l = l; tree[p].r = r;
if(l == r) return ;
build(l, mid, ls); build(mid+1, r, rs);
}
int up(int p, double k) {
if(tree[p].l == tree[p].r) return tree[p].maxx > k;
if(tree[ls].maxx <= k)
return up(rs, k);
return tree[p].ans + up(ls, k) - tree[ls].ans;
}
void update(int p, int pos, double k) {
int l = tree[p].l, r = tree[p].r;
if(l == r) {
tree[p].maxx = k; tree[p].ans = 1;
return ;
}
if(pos <= mid) update(ls, pos, k);
else update(rs, pos, k);
tree[p].maxx = max(tree[ls].maxx, tree[rs].maxx);
tree[p].ans = tree[ls].ans + up(rs, tree[ls].maxx);
}
LL read() {
int k = 0, f = 1; char c = getchar();
while(c < '0' || c > '9') {
if(c == '-') f = -1;
c = getchar();
}
while(c >= '0' && c <= '9')
k = k*10+c-48, c=getchar();
return k*f;
}
int main(){
int n = read(), m = read();
build(1, n, 1);
for(int i = 1; i <= m; ++i) {
int pos=read(), k=read();
update(1, pos, (double)k/pos);
printf("%d
", tree[1].ans);
}
return 0;
}
例3
给定(n)个数组成的数列(a),维护(q)个询问
- 区间加
- 区间除(下取整)
- 求区间最小值
- 求区间和
(n,q leq 10^5)
题解
每次区间加只会改变两端点处的差值,而我们的除法能够以指数级的速度将差值减小
如果区间([l,r])的最大最小值满足
说明差值最大的两个数的结果都相等,更何况其他数呢?此时直接用区间加就可以
如果不满足以上条件,就递归左右子树进行更改
例4
给定(n)个数组成的数列(a),支持以下操作:
- 区间求和
- 区间取模
- 区间赋值
(n,q ≤ 10^5)
题解
考虑把一串相同的数字叫做一段,那么一次赋值操作最多增加(2)段,总段数是 (O(q + n)) 的
直接用线段树维护,如果一段区间全部相同就直接区间赋值,否则递归取模。
每次取模,设为(x mod y)
当(y leq frac{x}{2}),取模完毕之后会小于 (frac{x}{2})
当(y geq frac{x}{2}) ,取模完毕之后也会小于 (frac{x}{2})
因此一段最多被取模(O(logn))次
总时间复杂度为(O((n + q)log^2 n))
例5
给出若干条二维平面上的线段, 用 ((x_1,y_1),(x_2,y_2)) 表示其两端点 坐标, 现在要求支持两种操作:
- (0; x_1; y_1; x_2; y_2):表示加入一条新的线段 ((x_1,y_1)−(x_2,y_2))
- (1;x_0):询问所有线段中, (x) 坐标在 (x_0) 处的最高点的 (y) 坐标是什么, 如果对应位置没有线段, 则输出 (0)
(m ≤ 2×10^5)
题解
开一棵以 (x) 坐标为关键字的线段树, 其中每个线段树节点存储一个线段。然后插入就直接定位(log n)个区间插入
如果这个点 ([l,r]) 已经有一条线段了, 那么注意到一定有一条线段会在 ([l,mid]) 或是 ([mid + 1,r]) 中一直是最大值。所以找出这条线段(比一下中点对应的的 (y) 就好了), 然后这个点保留这条线段, 另一条线段下传到里一个点对应的一个儿子
注意到询问只能是整数, 所以当我们到达底层节点还有线段需要下传时, 可以直接忽略掉
例6 (Segment tree Beats)
题解
可以用一种很神奇的线段树——(Segment; tree; Beats)来维护。
线段树上每个节点维护这个区间的最大值(max,) 次大值 (sec,) 最大值个数 (tot,) 区间和 (sum)
每次对整个区间取 (min (Ai,x)) 的时候分 (3) 种情况讨论:
- (x ≥ max,) 不用管
- (sec < x < max,) 可以直接维护 sum
- (x ≤ sec,) 递归处理
时间复杂度最坏可能是(O(n log^2 n)),不过很难跑满,大多数情况下是(O(n log n))
主席树
之前立下(flag),过年前不学新算法
才不是因为我懒
之后会单开一篇博客去写的(一定会的!)
Day 4
上午+下午——图论
最小生成树
例1
神仙做法
题解
我们给每条白边的边权都加上(mid),显然,随着(mid)增大,白边会变少,而(mid)减小,相应的,白边会增多。所以可知它具有单调性,所以我们就可以二分(mid)。直到白边的数目等于(need)
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int read() {
int k = 0, f = 1; char c = getchar();
while(c < '0' || c > '9') {
if(c == '-') f = -1;
c = getchar();
}
while(c >= '0' && c <= '9')
k = k * 10 + c - 48, c = getchar();
return k * f;
}
struct zzz {
int f, t, len, col;
}e[100010];
bool cmp(zzz x, zzz y) {
return x.len == y.len ? x.col < y.col : x.len < y.len;
}
int x[100010], y[100010], c[100010], col[100010], fa[50010];
int find(int x) {
return fa[x] == x ? x : fa[x] = find(fa[x]);
}
int n, m, need, cnt, ans, flag, sum;
bool check(int mid) {
flag = sum = 0;
for(int i = 1; i <= n; ++i) fa[i] = i;
for(int i = 1; i <= m; ++i) {
e[i].f = x[i], e[i].t = y[i], e[i].len = c[i], e[i].col = col[i];
if(!col[i]) e[i].len += mid;
}
sort(e+1, e+m+1, cmp);
for(int i = 1; i <= m; ++i) {
int xx = find(e[i].f), yy = find(e[i].t);
if(xx == yy) continue;
fa[xx] = yy;
sum += e[i].len;
if(!e[i].col) ++flag;
}
return flag >= need;
}
int main(){
//freopen("4240.in", "r", stdin);
//freopen("4240.out", "w", stdout);
n = read(), m = read(), need = read();
for(int i = 1; i <= m; ++i)
x[i] = read() + 1, y[i] = read() + 1, c[i] = read(), col[i] = read();
int l = -110, r = 110;
while(l < r) {
int mid = (l + r) >> 1;
if(check(mid)) l = mid + 1, ans = sum - mid * need;
else r = mid;
}
printf("%d", ans);
return 0;
}
例2
JZOJ 5895 旅游(实在是找不到链接)
题目大意
给定(n)个点,(m)条边,其中第(i)条边的长度为(2 ^ i)
求一条从(1)号点出发,经过所有的边又回到(1)号点的路径,并使得这条路径上的边的长度之和最小
(n,m leq 100000)
题解
由欧拉回路的性质可知,每个点的度数都应为偶数,所以对于度数为奇数的点,我们可以加一条重边来将它补成偶数
接下来要考虑该补哪些边
因为第(i)条边的长度为(2 ^ i),所以一条长度大的边可能比其他所有边加起来还要大
那么我们跑一边最小生成树,然后在最小生成树上加边就好了
例3
题解
这道题生成树的权值的计算方法十分的诡异,但通过数学变形可以发现,其实一棵树的权值等价于 该树所有点的点权( imes)该点回到点1的路径的边权和
然后跑最短路就好了~
差分约束
例1
题解
x[i]表示选择一行,该行每个格子的权值减1的次数 - 选择一行,该行每个格子的权值加1的次数
y[i]表示选择一列, 该列每个格子的权值加1的次数 - 选择一列, 该列每个格子的权值减1的次数
每个约束条件即x[i]+c[i]=y[i]
然后跑差分约束就可以了
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
int read() {
int k = 0, f = 1; char c = getchar();
while(c < '0' || c > '9') {
if(c == '-') f = -1;
c = getchar();
}
while(c >= '0' && c <= '9')
k = k * 10 + c - 48, c = getchar();
return k * f;
}
struct zzz {
int t, len, nex;
}e[1000010 << 1];
int head[2010], tot;
void add(int x, int y, int z) {
e[++tot].t = y;
e[tot].len = z;
e[tot].nex = head[x];
head[x] = tot;
}
int vis[2010], cnt[2010], dis[2010];
bool SPFA(int i, int lim) {
queue <int> q;
q.push(i); ++cnt[i], vis[i] = 1;
while(!q.empty()) {
int k = q.front(); q.pop(); vis[k] = 0;
if(cnt[k] > lim) return 0;
for(int i = head[k]; i; i = e[i].nex) {
if(dis[k] + e[i].len < dis[e[i].t]) {
dis[e[i].t] = dis[k] + e[i].len;
if(!vis[e[i].t])
vis[e[i].t] = 1, q.push(e[i].t), ++cnt[e[i].t];
}
}
}
return 1;
}
int main() {
int t = read();
while(t--) {
memset(head, 0, sizeof(head));
memset(cnt, 0, sizeof(cnt)); tot = 0;
int n = read(), m = read(), k = read();
for(int i = 1; i <= k; ++i) {
int a = read(), b = read(), c = read();
add(a, b+n, c); add(b+n, a, -c);
}
bool flag = 1;
for(int i = 1; i <= n+m; ++i)
if(!cnt[i]) if(!SPFA(i, n+m)) flag = 0;
if(flag) printf("Yes
");
else printf("No
");
}
return 0;
}
例2
题解
sum[i]表示前缀和,对于每个推测,就相当于sum[r[i]] - sum[l[i]-1] = s[i]
所以sum[r[i]] - sum[l[i]-1] <= s[i], sum[l[i]-1] - sum[r[i]] <= -s[i]
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
int read() {
int k = 0, f = 1; char c = getchar();
while(c < '0' || c > '9') {
if(c == '-') f = -1;
c = getchar();
}
while(c >= '0' && c <= '9')
k = k * 10 + c - 48, c = getchar();
return k * f;
}
struct zzz {
int t, len, nex;
}e[1010 << 1];
int head[110], tot;
void add(int x, int y, int z) {
e[++tot].t = y;
e[tot].len = z;
e[tot].nex = head[x];
head[x] = tot;
}
int vis[110], cnt[110], dis[110];
bool SPFA(int i, int lim) {
queue <int> q;
q.push(i); ++cnt[i], vis[i] = 1;
while(!q.empty()) {
int k = q.front(); q.pop(); vis[k] = 0;
if(cnt[k] >= lim) return 0;
for(int i = head[k]; i; i = e[i].nex) {
if(dis[k] + e[i].len < dis[e[i].t]) {
dis[e[i].t] = dis[k] + e[i].len;
if(!vis[e[i].t])
vis[e[i].t] = 1, q.push(e[i].t), ++cnt[e[i].t];
}
}
}
return 1;
}
int main() {
int t = read();
while(t--) {
memset(head, 0, sizeof(head));
memset(cnt, 0, sizeof(cnt)); tot = 0;
int n = read()+1, m = read();
for(int i = 1; i <= m; ++i) {
int a = read()+1, b = read()+1, c = read();
add(a-1, b, c); add(b, a-1, -c);
}
bool flag = 1;
for(int i = 1; i <= n; ++i)
if(!cnt[i]) if(!SPFA(i, n)) {flag = 0; break;}
if(flag) printf("true
");
else printf("false
");
}
return 0;
}
例3
sum[i]表示(0)~(i)至少有多少个元素被选择
对于每个条件我们可以写出如下等式:
sum[b] - sum[a] >= c
有因为这道题目的特殊性质,还有如下等式
sum[i] - sum[i-1] >= 0
sum[i] - sum[i-1] <= 1
Day 5/6
全是DP
讲的内容与之前整理的这篇Blog高度重合,所以就不想再整理了……
Day 7
Noip真题
额,还是不想整了……