我回来了...
本来是应该12月发的blog,没想到拖到了现在,注意事项什么的稍微有点忘了,以后再慢慢补充吧
点分治是一种树上算法。顾名思义,就是对每个点进行分治,计算它的子树对答案的贡献。
主要用于处理树上路径,且一个点会被统计多次的问题。
以这道题为例:
询问树上距离为k的点对是否存在。
设当前的根节点为x。
若距离为k的点对存在,有两种情况:经过x和不经过x。
经过时,若x的两个相异的子树中的两个点到x的距离之和=k,
即x有子树A,B,...,若有(x,Ai)+(x,Bj)=k,则x对答案做出了贡献。
不经过时,则对x的每一个子树递归分治处理。
但是,在统计答案的过程中,难免会计算x的同一子树中的情况,即(x,Ai)+(x,Aj)=k
Ai到Aj的距离应该在子树A中计算,否则它们间的距离会被加上重复的路径
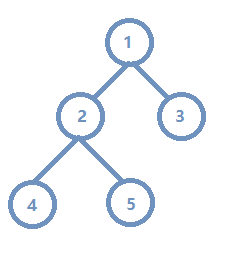
比如上图中统计1的答案会计算(1,4)+(1,5),其中路径(1,2)被加了两次。
实际上(4)到(5)的距离不是4而是2。
因此,计算完当前节点的答案后,还要减去它的子树的重复答案。具体步骤在后面详细说明。
可以发现,时间复杂度由x的子树大小决定。
使x的最大子树最小——x是树的重心。
所以,递归处理每一棵子树时,都要找到它的重心作为根节点。
综上所述,点分治的步骤可以概括为:
(root:当前重心)
找root,处理root[
计算root的贡献,遍历root的子树( 对于每棵子树:
减去该子树中的重复计算,
找该子树root,处理root[...]
)
]
在这里一共用到了四个函数:
get_rt() —— 找root
divide() —— 分治处理
calc() —— 计算贡献
dfs() —— 递归求深度,用来计算路径长(根据每道题题意不同)。
vis[x]表示x是否被分治处理过。
因为分治的过程中可能会把树旋转成不同的形状,
或者说,因为根变化了,已经统计完的点可能会在新的根节点下面。
这个变量只在divide()中更新,但是所有函数都要用到。
$get$_$rt()$
类似于树形dp,是一个递归找最大子树的过程。
siz[x]表示以x为根的子树大小(包括自己),
f[x]表示x的最大子树大小。
sum表示要求root的这部分子树的总点数,初始时为n。
某一点x的最大子树,其实不一定在x的下面,也可能是x作为根时x的父亲的那一部分子树。
所以除了每次f[u] = max(f[u],siz[v]),【注意这里不要误写成f[v]】
还要在最后更新f[u] = max(f[u],sum-siz[u])。
void get_rt(int u,int fa) { siz[u] = 1; f[u] = 0; for(int i = head[u]; i; i = nxt[i]) { int v = to[i]; if(v == fa || vis[v]) continue; get_rt(v,u); siz[u] += siz[v]; f[u] = max(f[u],siz[v]); } f[u] = max(f[u],sum-siz[u]); if(f[u] <= f[rt]) rt = u; }
$divide()$
首先将这个点标记vis,表示已经分治过了。
计算它的贡献。
传入$calc$的三个参数(u,nowdis,op)分别表示当前点、到这个点为止已经走过的距离、是加入还是减去这个点的贡献(加入为1,减去为-1)。
遍历这个点的儿子时,首先判断是否vis过;
减去这个子树内部的重复计算:nowdis为边(u,v)的权值,op为-1.
然后处理这棵子树。
子树的总点数sum即为siz[v](在上次get_rt中已经算好了),rt=0,f[0]=MAX(这里可以是siz[v])
在这棵子树中找到重心,并分治。
因为这次的操作是局限在这个子树中的,所以并不会影响到它的兄弟,并列操作即可。
void divide(int u) { vis[u] = true; calc(u,0,1); for(int i = head[u]; i; i = nxt[i]) { int v = to[i]; if(vis[v]) continue; calc(v,w[i],-1); rt = 0,f[0] = sum = siz[v]; get_rt(v,u); divide(rt); } }
$calc()$
前面已经提到了calc中的三个参数:(u,nowdis,op)
tot表示所要计算的子树中的总点数,在dfs时计算。
dfs中传入的参数分别为(u,fa,nowdis),含义相同
dfs完毕后,n^2枚举点对,计算它们的贡献。
ans[x]表示距离为x的点对个数;
dis[i]表示从该子树根节点到i的距离。
根据op的值不同,答案+1或-1。
void calc(int u,int nowdis,int op) { tot = 0; dfs(u,0,nowdis); for(int i = 1; i <= tot; i++) for(int j = i+1; j <= tot; j++) ans[dis[i]+dis[j]] += op; }
$dfs()$
根据题意,在dfs中求出该子树根节点到子树中个点的距离。
利用tot,给子树中的点重新编号1~tot,同时求出总点数。
到达某个点时,编号为++tot,且该点的dis即为nowdis.
然后再遍历这个点的儿子节点并dfs;
同样为了防止重复,要先判断是否vis过。
新的nowdis即为原来的nowdis+w(u,v).
void dfs(int u,int fa,int nowdis) { dis[++tot] = nowdis; for(int i = head[u]; i; i = nxt[i]) { int v = to[i]; if(v == fa || vis[v]) continue; dfs(v,u,nowdis+w[i]); } }
最后对于每个询问k,检查ans[k]是否大于0即可。
总结一下:
初始化:f[0] = sum = n,get_rt(1,0),divide(root);
$get$_$rt$(int u,int fa) 递归 需判断(v == fa || vis[v])
$divide$(int u) 递归 更新vis[u],需判断(vis[v])
$calc$(int u,int nowdis,int op) 无递归,无判断
$dfs$(int u,int fa,int nowdis) 递归 需判断(v == fa || vis[v])
完整代码如下

#include<cstdio> #include<iostream> #include<cmath> #include<cstring> #define MogeKo qwq using namespace std; const int maxn = 20005; int n,m,x,y,z,ans[10000005]; int rt,sum,tot,siz[maxn],f[maxn],dis[maxn]; int cnt; int head[maxn],to[maxn],nxt[maxn],w[maxn]; bool vis[maxn]; int read() { int x = 0,f = 1; char ch = getchar(); while(ch < '0' || ch > '9') { if(ch == '-') f = -1; ch = getchar(); } while('0' <= ch && ch <= '9') { x = (x<<3) + (x<<1) + ch-'0'; ch = getchar(); } return x*f; } void add(int x,int y,int z) { to[++cnt] = y; nxt[cnt] = head[x]; head[x] = cnt; w[cnt] = z; } void dfs(int u,int fa,int nowdis) { dis[++tot] = nowdis; for(int i = head[u]; i; i = nxt[i]) { int v = to[i]; if(v == fa || vis[v]) continue; dfs(v,u,nowdis+w[i]); } } void calc(int u,int nowdis,int op) { tot = 0; dfs(u,0,nowdis); for(int i = 1; i <= tot; i++) for(int j = i+1; j <= tot; j++) ans[dis[i]+dis[j]] += op; } void get_rt(int u,int fa) { siz[u] = 1; f[u] = 0; for(int i = head[u]; i; i = nxt[i]) { int v = to[i]; if(v == fa || vis[v]) continue; get_rt(v,u); siz[u] += siz[v]; f[u] = max(f[u],siz[v]); } f[u] = max(f[u],sum-siz[u]); if(f[u] <= f[rt]) rt = u; } void divide(int u) { vis[u] = true; calc(u,0,1); for(int i = head[u]; i; i = nxt[i]) { int v = to[i]; if(vis[v]) continue; calc(v,w[i],-1); rt = 0,f[0] = sum = siz[v]; get_rt(v,u); divide(rt); } } int main() { scanf("%d%d",&n,&m); for(int i = 1; i <= n-1; i++) { x = read(),y = read(),z = read(); add(x,y,z); add(y,x,z); } f[0] = sum = n; get_rt(1,0); divide(rt); for(int i = 1; i <= m; i++) { x = read(); if(ans[x]) printf("AYE "); else printf("NAY "); } return 0; }
