概念
无向图的割:有无向图G=(V,E)G=(V,E),设CC为图GG中一些弧的集合,若从GG中删去CC中的所有弧能使图GG不是连通图,称CC图GG的一个割。
S−T割:使得顶点SS与顶点TT不再连通的割,称为S−T割
S−T最小割:包含的弧的权和最小的S−T割,称为S−T最小割。
全局最小割:包含的弧的权和最小的割,称为全局最小割。
首先我们知道
对于图的任意两个顶点s、t,要么在全局最小割的同一个集合中,要么在不同的集合中。那么结果便只可能在是s-t最小割,或者合并s和t的新图的全局最小割。
Stoer-Wagner算法就是用来求全局最小割的算法,简称SW算法。
算法步骤如下:
(1)min=MAXINT,固定一个顶点P
(2)从点P用类似prim的s算法扩展出“最大生成树”,记录最后扩展的顶点和最后扩展的边
(3)计算最后扩展到的顶点的切割值(即与此顶点相连的所有边权和),若比min小更新min
(4)合并最后扩展的那条边的两个端点为一个顶点
(5)转到2,合并N-1次后结束
(6)min即为所求,输出min
任选一个点P,初始化wage数组的值都是0,开始遍历扩展,并且把点P放入了已扩展点的集合;找到与P相连的权值最大的节点,并更新与p相连的节点的wage数组值。下一次就选取wage数组最大值的点(也就是点4)开始向外扩展,注意在扩展点4的时候点P不会再被更新,因为它已经进入被扩展集合了。过程同上。
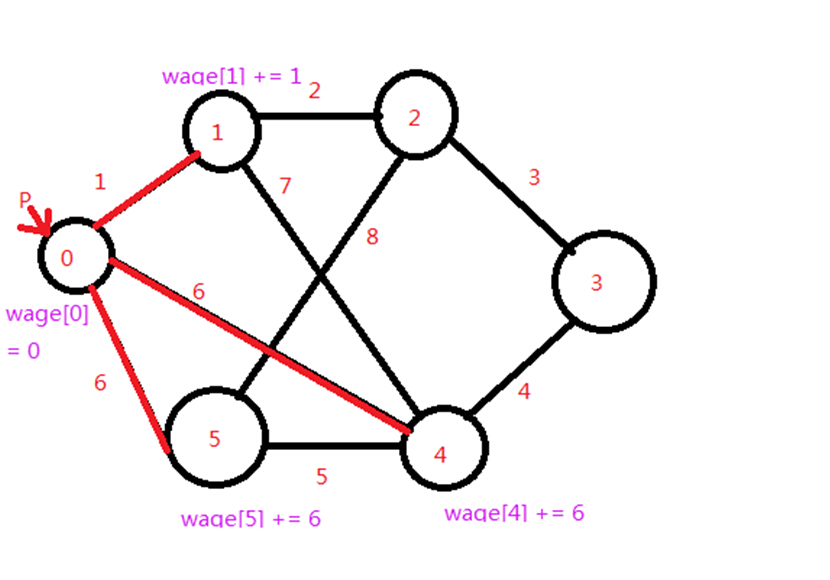
一直扩展。。。扩展到最后两个点的时候我们记为S,T;其中T是最后一个点;这时候我们得到了wage[S] 和 wage[T];
现在有如下性质:
1、wage[T]是将单点T分离出原图的最小的割的值(这里说的是把T这个点单独拿出去);
2、wage[T]的值是将S或T单独分离出原图的最小割值中较小的那一个;即wage[T]<=wage[S]
下面给出一些问题的证明:
(1)上面性质2的证明
分为两种情况,第一,S与T有边相连时,假设该边的权值为k。在通过S进行扩展时,由于先选择S,所以可以得到扩展前wage[S]>=wage[T] 。在扩展时 wage[T]的值必然会增加S与T之间的权值,即wage[T]=wage[T]+k。但是这个权值也是属于S的,wage[S]=wage[S]+k, 所以相加同一个数后不等式仍然成立;
同理S,T无边相连也可以仿照上面的解释;
(2)我们任意找两个点,比较wage的大小,行不行
证明合并两个点的操作不会影响最终的答案,说明这个问题前,我们先进行下面的一个讨论。
到目前为止好像对于我们有用处的就是最后那两个点S,T。我们不禁要问下,如果只是为了选出两个点,有必要这么麻烦吗(最大生成树)?直接随意选两个点,计算出对应的wage的值,即计算把他们单独分割出去的值,比较大小,小的记为T大的记为S,然后更新min。好像也满足了上面所要的结果。显然这么做不对。
我们考虑下面一种情况
我们先来想一想分割后的情况,假设我们找到了原图的最小割然后按照最小割集进行分割,那么原图一定被分为两部分且只能是两部分,记为A,B ;A,B彼此连同,分割后的A,B 显然是不连通的。为了简化证明过程我假设 原图A与B 仅有一条边相连。当然这条边的值就是最小割的值。
这条边连接的两个点一个在A中一个在B中 分别记为a,b。如果A中或B中只有一个点,那么你按照随意选点的方法不会影响最后的答案,我们这里要讨论A和B中点的个数大于1。这时如果你还随意的找两个点进行更新min 合点操作就会出错了。
这很好想,因为如果你一开始选的是a,b 两个点,那么你计算出的wage肯定是大于最小割,因为无论a,b都肯定与至少2个点相连,而最终的答案是a,b间边的权值。
这时如果把a,b合点后再进行上面的重复操作显然已经把最佳答案错过了。
(3)证明prim确定一个顺序问题,我还以这个例子来说,通过prim选出的两个点S,T一定都在A中或者在B中(前提是A,B中包含2个或以上的点)也只有在这个前提下进行点的合并才不会影响最后的答案。
我们先来证明下这两个点一定在一边而不会是一边一个(前提是A,B中包含2个或以上的点)
证明:首先我们不妨设prim 过程的第一个点在A中,那么它一定先在A中的点开始扩展操作,进行prim扩展若干次后,才首次计算B中点的wage 。这个时候一定是A,B相连的那个点,此时wage[b]的值为最小割的值。
那么就可以分为多种情况
1、A中的节点扩展完才扩展B的节点。由于是prim是从大到小来扩展的,即这种情况下,A中可扩展的点的wage值都大于wage[b],这样不会再回A中了,那么最后的两个点一定都在B中。(如果从B中开始,最后两个节点在A中)
2、在A中扩展多次之后去B中扩展,反复下去,最终到B中。因为如果最后的点在B中,而且B中不止一个点,肯定至少经历了一次从A到B,从B到A,再从A到B的过程。如果一直在A中那么最后的点在B中,如果再次回到B中扩展可知此时A中可扩展的点的wage值都小于B中可扩展点的wage值,反复反复下去,
如果最后A中一个点,B中一个点,会出现什么情况呢?显然最后的那个点的wage值小于wage[b]了。这样更新完原图的最小割更小了,这显然矛盾了。
矛盾的原因就在于prim的过程根本就没法实现一个在A中一个在B中。
如果S,T相连, 我已经更新了将S,T分割单独分割出去时最小割的值,那么现在即使将S和T合并也不会影响全局最小割的求解。
如果S,T不直接相连时,如果答案是S,T合并后的解显然将两者一起分离的时候已经将T单独分开了。所以将S和T合并,并不会影响后面的计算。
合点操作之所以不影响答案的关键是prim算法的步骤决定了选点的顺序。
下面的代码是SW算法的代码,不过每次都是从第0个节点扩展的,最终来得到全局最小割。
#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> using namespace std; #define MAX_N 30 #define INF 0x3f3f3f3f int G[MAX_N][MAX_N]; int v[MAX_N]; // v[i]代表节点i合并到的顶点 int w[MAX_N]; // 定义w(A,x) = ∑w(v[i],x),v[i]∈A bool visited[MAX_N]; // 用来标记是否该点加入了A集合 int squ[MAX_N]; //记录移除的节点次序 int index;//记录最小割的位置,以便分开整个图的节点 int stoer_wagner(int n) { int min_cut = INF,r=0; for (int i = 0; i < n; ++i) { v[i] = i; // 初始还未合并,都代表节点本身 } while (n > 1) { int pre = 0; // pre用来表示之前加入A集合的点(在t之前一个加进去的点) memset(visited, 0, sizeof(visited)); memset(w, 0, sizeof(w)); for (int i = 1; i < n; ++i) //求出 某一轮最大生成树的最后两个节点,并且去除最后的t,将与t连接的边归并 { int k = -1; for (int j = 1; j < n; ++j) // 选取V-A中的w(A,x)最大的点x加入集合 { if (!visited[v[j]]) { w[v[j]] += G[v[pre]][v[j]]; if (k == -1 || w[v[k]] < w[v[j]]) { k = j; } } } visited[v[k]] = true; // 标记该点x已经加入A集合 if (i == n - 1) // 若|A|=|V|(所有点都加入了A),结束 { const int s = v[pre], t = v[k]; // 令倒数第二个加入A的点(v[pre])为s,最后一个加入A的点(v[k])为t cout<<t<<"--->"<<s<<endl; squ[r++]=t; if(w[t]<min_cut) { min_cut=w[t]; index=r; } //min_cut = min(min_cut, w[t]); // 则s-t最小割为w(A,t),用其更新min_cut for (int j = 0; j < n; ++j) // Contract(s, t) { G[s][v[j]] += G[v[j]][t]; G[v[j]][s] += G[v[j]][t]; } v[k] = v[--n]; // 删除最后一个点(即删除t,也即将t合并到s) } // else 继续 pre = k; } } return min_cut; } int main(int argc, char *argv[]) { int n, m; while (scanf("%d%d", &n, &m) != EOF) { memset(G, 0, sizeof(G)); while (m--) { int u, v, w; scanf("%d%d%d", &u, &v, &w); G[u][v] += w; G[v][u] += w; } int z=n; //printf("%d ", stoer_wagner(n)); cout<<" 归并的步骤为:"<<endl; int res=stoer_wagner(n); cout<<" 最小割的总权值为: "<<res<<" 图划分为部分A:"; //cout<<"图划分为部分A:"; for(int i=0;i<z;i++) { if(i==index) cout<<"部分B:"; cout<<squ[i]<<" "; } } return 0; }