第五周-梯度下降

   机器学习中的大部分问题都是优化问题，而绝大部分优化问题都可以使用梯度下降法处理，那么搞懂什么是梯度，什么是梯度下降法就非常重要！提到梯度，就必须从导数（derivative）、偏导数（partial derivative）和方向导数（directional derivative）讲起，弄清楚这些概念，才能够正确理解为什么在优化问题中使用梯度下降法来优化目标函数，并熟练掌握梯度下降法（Gradient Descent）。

一.梯度下降

  

      通过上面的图形和导数的定义，可以看出导数反映的是函数y=f(x)在某一点处沿x轴正方向的变化率，是函数f(x)在x轴上某一点处沿着x轴正方向的变化率/变化趋势。直观地看，也就是在x轴上某一点处，如果f'(x)>0，说明f(x)的函数值在x点沿x轴正方向是趋于增加的；如果f'(x)<0，说明f(x)的函数值在x点沿x轴正方向是趋于减少的。补充上图中的Δy、dy等符号的意义及关系如下： 

   Δx：x的变化量；

 　dx：x的变化量Δx趋于0时，则记作微元dx； 

　 Δy：Δy=f(x0+Δx)-f(x0)，是函数的增量；
　 dy：dy=f'(x0)dx，是切线的增量；
　 当Δx→0时，dy与Δy都是无穷小，dy是Δy的主部，即Δy=dy+o(Δx)。
   偏导数的定义如下：

    导数与偏导数本质是一致的，都是当自变量的变化量趋于0时，函数值的变化量与自变量变化量比值的极限。直观地说，偏导数也就是函数在某一点上沿坐标轴正方向的的变化率。 其区别在于，导数，指的是一元函数中，函数y=f(x)在某一点处沿x轴正方向的变化率；偏导数，指的是多元函数中，函数y=f(x1,x2,…,xn)在某一点处沿某一坐标轴（x1,x2,…,xn）正方向的变化率。

   方向导数的定义如下： 

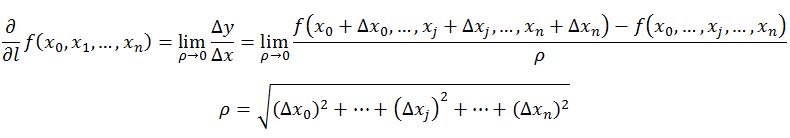
    在前面导数和偏导数的定义中，均是沿坐标轴正方向讨论函数的变化率。那么当我们讨论函数沿任意方向的变化率时，也就引出了方向导数的定义，即：某一点在某一趋近方向上的导数值。通俗的解释是，　我们不仅要知道函数在坐标轴正方向上的变化率（即偏导数），而且还要设法求得函数在其他特定方向上的变化率。而方向导数就是函数在其他特定方向上的变化率。 

   梯度的定义如下：

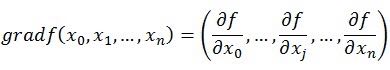
  梯度的提出只为回答函数在变量空间的某一点处，沿着哪一个方向有最大的变化率。其定义为函数在某一点的梯度是这样一个向量，它的方向与取得最大方向导数的方向一致，而它的模为方向导数的最大值。
　这里需注意以下三点：

• 　梯度是一个向量，即有方向有大小；
• 　梯度的方向是最大方向导数的方向；
• 　梯度的值是最大方向导数的值。

  向量的定义是有方向（direction）有大小（magnitude）的量。 从前面的定义可以这样看出，偏导数和方向导数表达的是函数在某一点沿某一方向的变化率，也是具有方向和大小的。因此从这个角度来理解，我们也可以把偏导数和方向导数看作是一个向量，向量的方向就是变化率的方向，向量的模，就是变化率的大小。 那么沿着这样一种思路，就可以如下理解梯度，梯度即函数在某一点最大的方向导数，函数沿梯度方向函数有最大的变化率。

  既然在变量空间的某一点处，函数沿梯度方向具有最大的变化率，那么在优化目标函数的时候，自然是沿着负梯度方向去减小函数值，以此达到我们的优化目标。如何沿着负梯度方向减小函数值呢？既然梯度是偏导数的集合，如下：

既然在变量空间的某一点处，函数沿梯度方向具有最大的变化率，那么在优化目标函数的时候，自然是沿着负梯度方向去减小函数值，以此达到我们的优化目标。 
　如何沿着负梯度方向减小函数值呢？既然梯度是偏导数的集合，如下：

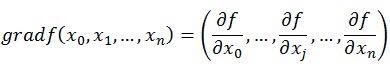
  同时梯度和偏导数都是向量，那么参考向量运算法则，我们在每个变量轴上减小对应变量值即可，梯度下降法可以描述如下： 

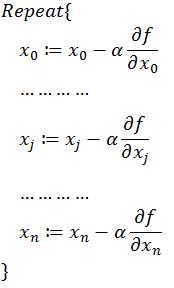
      以上就是梯度下降法的概念，大部分的机器学习任务，都可以利用Gradient Descent来进行优化。  

   梯度下降的一个直观的解释。比如我们在一座大山上的某处位置，由于我们不知道怎么下山，于是决定走一步算一步，也就是在每走到一个位置的时候，求解当前位置的梯度，沿着梯度的负方向，也就是当前最陡峭的位置向下走一步，然后继续求解当前位置梯度，向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去，一直走到觉得我们已经到了山脚。当然这样走下去，有可能我们不能走到山脚，而是到了某一个局部的山峰低处。可以看出，梯度下降不一定能够找到全局的最优解，有可能是一个局部最优解。当然，如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解，下图便于更加形象地理解。

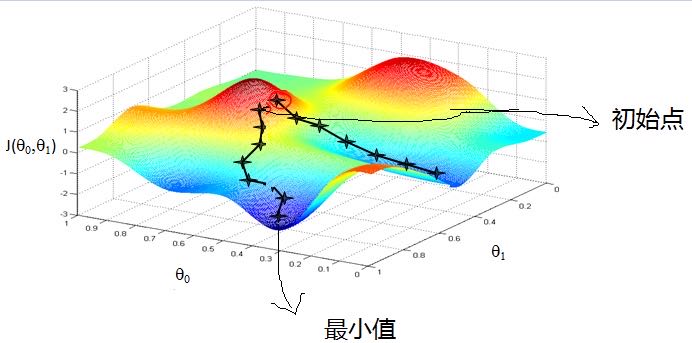
二.常用的梯度下降算法

   在实际应用的过程中，梯度下降算法有三类，它们不同之处在于每次学习(更新模型参数)使用的样本个数，每次更新使用不同的样本会导致每次学习的准确性和学习时间不同。

1. 批量梯度下降(Batch gradient descent) 

     每次使用全量的训练集样本来更新模型参数，即给定一个步长，然后对所有的样本的梯度的和进行迭代： 

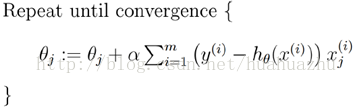
   梯度下降算法最终得到的是局部极小值。而线性回归的损失函数为凸函数，有且只有一个局部最小，则这个局部最小一定是全局最小。所以线性回归中使用批量梯度下降算法，一定可以找到一个全局最优解。其优点主要体现在全局最优解；易于并行实现；总体迭代次数不多，但当样本数目很多时，训练过程会很慢，每次迭代需要耗费大量的时间。

2.随机梯度下降(Stochastic gradient descent) 

    随机梯度下降算法每次从训练集中随机选择一个样本来进行迭代，即：

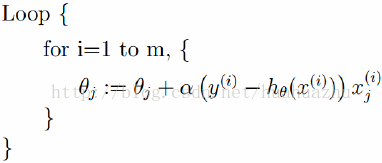
    随机梯度下降算法每次只随机选择一个样本来更新模型参数，因此每次的学习是非常快速的，并且可以进行在线更新。 随机梯度下降最大的缺点在于每次更新可能并不会按照正确的方向进行，因此可以带来优化波动(扰动)。不过从另一个方面来看，随机梯度下降所带来的波动有个好处就是，对于类似盆地区域（即很多局部极小值点）那么这个波动的特点可能会使得优化的方向从当前的局部极小值点跳到另一个更好的局部极小值点，这样便可能对于非凸函数，最终收敛于一个较好的局部极值点，甚至全局极值点。其优点是训练速度快，每次迭代计算量不大，但准确度下降，并不是全局最优；不易于并行实现；总体迭代次数比较多。

3.Mini-batch梯度下降算法

    Mini-batch梯度下降综合了batch梯度下降与stochastic梯度下降，在每次更新速度与更新次数中间取得一个平衡，其每次更新从训练集中随机选择b,b<m个样本进行学习，即：

三，梯度算法的Python代码实现

 1,批量梯度下降算法

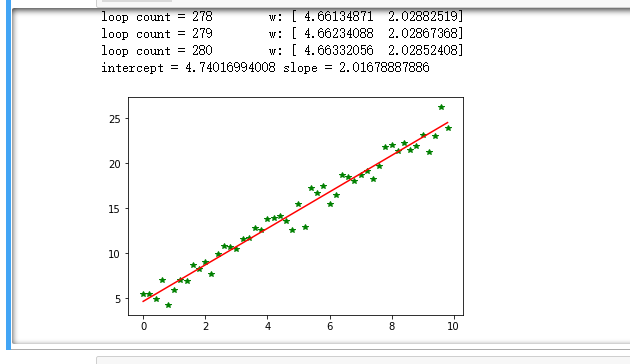
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
# 构造训练数据
x = np.arange(0., 10., 0.2)
m = len(x)  # 训练数据点数目
print(m)
x0 = np.full(m, 1.0)
input_data = np.vstack([x0, x]).T  # 将偏置b作为权向量的第一个分量
target_data = 2 * x + 5 + np.random.randn(m)
# 两种终止条件
loop_max = 10000  # 最大迭代次数(防止死循环)
epsilon = 1e-3
# 初始化权值
np.random.seed(0)
theta = np.random.randn(2)
alpha = 0.001  # 步长(注意取值过大会导致振荡即不收敛,过小收敛速度变慢)
diff = 0.
error = np.zeros(2)
count = 0  # 循环次数
finish = 0  # 终止标志
while count < loop_max:
    count += 1

    # 标准梯度下降是在权值更新前对所有样例汇总误差，而随机梯度下降的权值是通过考查某个训练样例来更新的
    # 在标准梯度下降中，权值更新的每一步对多个样例求和，需要更多的计算
    sum_m = np.zeros(2)
    for i in range(m):
        dif = (np.dot(theta, input_data[i]) - target_data[i]) * input_data[i]
        sum_m = sum_m + dif  # 当alpha取值过大时,sum_m会在迭代过程中会溢出

    theta = theta - alpha * sum_m  # 注意步长alpha的取值,过大会导致振荡
    # theta = theta - 0.005 * sum_m      # alpha取0.005时产生振荡,需要将alpha调小

    # 判断是否已收敛
    if np.linalg.norm(theta - error) < epsilon:
        finish = 1
        break
    else:
        error = theta
    print('loop count = %d' % count, '	w:',theta)
print('loop count = %d' % count, '	w:',theta)

# check with scipy linear regression
slope, intercept, r_value, p_value, slope_std_error = stats.linregress(x, target_data)
print('intercept = %s slope = %s' % (intercept, slope))

plt.plot(x, target_data, 'g*')
plt.plot(x, theta[1] * x + theta[0], 'r')
plt.show()

    运行结果如下：

2.随机梯度下降算法

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt

# 构造训练数据
x = np.arange(0., 10., 0.2)
m = len(x)  # 训练数据点数目
x0 = np.full(m, 1.0)
input_data = np.vstack([x0, x]).T  # 将偏置b作为权向量的第一个分量
target_data = 2 * x + 5 + np.random.randn(m)

# 两种终止条件
loop_max = 10000  # 最大迭代次数(防止死循环)
epsilon = 1e-3
# 初始化权值
np.random.seed(0)
theta = np.random.randn(2)
# w = np.zeros(2)
alpha = 0.001  # 步长(注意取值过大会导致振荡,过小收敛速度变慢)
diff = 0.
error = np.zeros(2)
count = 0  # 循环次数
finish = 0  # 终止标志
######-随机梯度下降算法
while count < loop_max:
    count += 1

    # 遍历训练数据集，不断更新权值
    for i in range(m):
        diff = np.dot(theta, input_data[i]) - target_data[i]  # 训练集代入,计算误差值

        # 采用随机梯度下降算法,更新一次权值只使用一组训练数据
        theta = theta - alpha * diff * input_data[i]

        # ------------------------------终止条件判断-----------------------------------------
        # 若没终止，则继续读取样本进行处理，如果所有样本都读取完毕了,则循环重新从头开始读取样本进行处理。

    # ----------------------------------终止条件判断-----------------------------------------
    # 注意：有多种迭代终止条件，和判断语句的位置。终止判断可以放在权值向量更新一次后,也可以放在更新m次后。
    if np.linalg.norm(theta - error) < epsilon:     # 终止条件：前后两次计算出的权向量的绝对误差充分小
        finish = 1
        break
    else:
        error = theta
print('loop count = %d' % count,  '	w:',theta)

# check with scipy linear regression
slope, intercept, r_value, p_value, slope_std_error = stats.linregress(x, target_data)
print('intercept = %s slope = %s' % (intercept, slope))

plt.plot(x, target_data, 'g*')
plt.plot(x, theta[1] * x + theta[0], 'r')
plt.show()

   运行代码显示结果如下。

 3.Mini-batch梯度下降

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt

# 构造训练数据
x = np.arange(0.,10.,0.2)
m = len(x)  # 训练数据点数目
print(m)
x0 = np.full(m, 1.0)
input_data = np.vstack([x0, x]).T  # 将偏置b作为权向量的第一个分量
target_data = 2 *x + 5 +np.random.randn(m)
# 两种终止条件
loop_max = 10000  #最大迭代次数(防止死循环)
epsilon = 1e-3
# 初始化权值
np.random.seed(0)
theta = np.random.randn(2)
alpha = 0.001  #步长(注意取值过大会导致振荡即不收敛,过小收敛速度变慢)
diff = 0.
error = np.zeros(2)
count = 0  #循环次数
finish = 0  #终止标志
minibatch_size = 5  #每次更新的样本数
while count < loop_max:
    count += 1

    # minibatch梯度下降是在权值更新前对所有样例汇总误差，而随机梯度下降的权值是通过考查某个训练样例来更新的
    # 在minibatch梯度下降中，权值更新的每一步对多个样例求和，需要更多的计算

    for i in range(1,m,minibatch_size):
        sum_m = np.zeros(2)
        for k in range(i-1,i+minibatch_size-1,1):
            dif = (np.dot(theta, input_data[k]) - target_data[k]) *input_data[k]
            sum_m = sum_m + dif  #当alpha取值过大时,sum_m会在迭代过程中会溢出

        theta = theta- alpha * (1.0/minibatch_size) * sum_m #注意步长alpha的取值,过大会导致振荡
    # 判断是否已收敛
    if np.linalg.norm(theta- error) < epsilon:
        finish = 1
        break
    else:
        error = theta
    print('loopcount = %d'% count, '	w:',theta)
print('loop count = %d'% count, '	w:',theta)

# check with scipy linear regression
slope, intercept, r_value, p_value,slope_std_error = stats.linregress(x, target_data)
print('intercept = %s slope = %s'% (intercept, slope))

plt.plot(x, target_data, 'g*')
plt.plot(x, theta[1]* x +theta[0],'r')
plt.show()

   运行代码显示结果如下：

     以上是第五周有关梯度下降算法的学习笔记，留作参考。