动态规划初探及什么是无后效性？ （转）

转自：http://www.cnblogs.com/yanlingyin/archive/2011/11/12/2246624.html

对于动态规划，我是这样理解的：
把待解决的问题分为一个规模较原问题小的子问题、

然后要考虑的就是如何更具这个子问题如何得到原问题的解以及如何解决这个子问题

当然、原问题和子问题需要有相同的解决方式、它们只有问题规模的区别。

这样讲有点抽象、用一个简单的图来说明下：

可以简单的这样理解、把原问题划分为小的问题（能组合成原问题的，小的问题再划分、持续下去，找到简单解

反方向计算回来（记下每一步结果）最后就能得到解。

听起来似乎不难，但是要作比较深入的理解还是得通过实例说话

有向无环图的最长简单路径：

对于一般的图，求最长路径并不向最短路径那样容易，因为最长路径并没有最优子结构的属性。但DGA例外

问题描述： 

给一个带权有向无环图G=（V，E），找出这个图里的最长路径。

说实话初学者直接给出这个图会看蒙的、再看看问题，不知道从何下手。

好了，对上图做个简单的处理：

现在看起来是不是清晰多了呢

用dilg(v)表示 以点结尾的最长路径，现在考虑dilg(D), dilg(B), dilg(C)

dilg(D)=max{dilg(B)+1, dilg(C)+3}

来解释一下：点D的入度边有CD、BD。

以D结尾的最短路径必定经过C、B中的一点；如果是C点，则以dilg(C)+3(权值)定会大于等于dilg(B)+1(权值)

如果没能看懂，请注意dilg(V)的定义

对于任意的点V可以有如下表达式：
      dilg(v)=max{dilg(u)+w(u, v)，(u,v)∈E}

这样、问题dilg(V)就会被转化为较小的子问题dilg(U)（当然，U是连入V的点）

任何一个问题都可以用这样的方式转化、变小。

但总不能无限变小啊，最后回成为最简单的问题。当有两个点，且其中的一个点入度为0的时候如图中的S-->C他们的最长距离就是

权值2。入门篇中说过，思考方向是从复杂到简单，而计算方向是从简单到复杂。

算法如下

Initialize all dilg(.) values to ∞;
1.Let S be the set of vertices with indegree=0;                       ////设集合S，里面的是入度为0的点
2.For each vertex v in S do　　　　　　　　　　　　
     dilg(v)=0;
3. For each v∈VS in Topological Sorting order do　　　　//对于V中除S外的点、按照拓扑排序的顺序，依次求出最长路径并保存好
       dilg(v)=max{dilg(u)+w(u, v)，(u,v)∈E}　　　　　　　　//拓扑排序可以简单的理解为从起点到终点的最短路径
4. Return the dilg(v) with maximum value.

现在是找到最长路径的大小了、但是如何得到最长路径呢？
只需做点小小的改动：

Dplongestpath(G)
Initialize all dilg(.) values to ∞;
Let S be the set of vertices with indegree=0;
for each vertex v in S do
     dist(v)=0;
4. For each v∈VS in Topological Sorting order do
       dilg(v)=max(u,v)∈E{dilg(u)+w(u, v)}
     let (u,v) be the edge to get the maximum    
     value;
     dad(v)=u;
5. Return the dilg(.) with maximum value.

 每一步都记下V的父节点、最后根据dad()数组即可得到路径。

对于上面的问题：先找出子问题、然后解决由子问题如何得到父问题以及如何把子问题分为更小的子问题

注意：问题的本质没有改变，只是规模变小。

我的理解：

动态规划的目的正是在不改变问题本质的情况下不断缩小子问题的规模、规模很小的时候，也就能很容易得到解啦（正如上面的只有两个点的情况）

上图可以这样理解：

问题A5被分成了子问题A3、A4解决它们就能解决A5，由于A3、A4和A5有相同的结构（问题的本质没变）所以A3可以分为问题A1、A2。当然A4也能

分为两个子问题，只是图中没画出来。

下面的是再网上看到的不错的思路： 

Dynamic programming:
(1)problem is solved by identifying a collection of   
    subproblems,
(2) tackling them one by one, smallest rst,
(3) using the answers of small problems to help 
     figure out larger ones,
(4) until the whole lot of them is solved.

 下面转自：http://blog.csdn.net/qq_30137611/article/details/77655707

初探动态规化

刚学动态规划，或多或少都有一些困惑。今天我们来看看什么是动态规划，以及他的应用。
学过分治方法的人都知道，分治方法是通过组合子问题来求解原问题，而动态规划与分治方法相似，都是通过组合子问题的解来求解原问题，不同的是分治每次都产生一个新的子问题，而动态规划会不一定产生新问题，可能产生重叠的子问题，即不同的子问题有公共的子子问题。
说了这么多的比较苦涩的话，只是为了回头再看，我们通过一个例子来具体说明一下：

钢条切割问题

小王刚来到一家公司，他的顶头boss买了一条长度为10的钢条，boss让小王将其切割为短钢条，使得这条钢条的价值最大，小王应该如何做？我们假设切割工序本身没有成本支出。
已知钢条的价格表如下：

长度 i	1	2	3	4	5	6	7	8	9	10
价格P(i)	1	5	8	9	10	17	17	20	24	30

小王是一个非常聪明的人，立刻拿了张纸画了一下当这根钢条长度为4的所有切割方案(将问题的规模缩小)

小王很快看出了可以获得的最大收益为5+5=10，他想了想，自己画图以及计算最大值的整个流程，整理了一下：
1>先画出切一刀所有的切割方案：（1+8）、（5+5）、（8+1）一共三种可能，也就是 4 - 1中可能，把这个 4 换成 n（将具体情况换成一般情况）,就变成了长度为 n 的钢条切一刀会有 n -1 中可能，然后在将一刀切过的钢条再进行切割。
同上，（1+8）这个组合会有 2 中切法，（1+1+5）和（1+5+1）【看图】，同理，（5+5）会有两种切法（1+1+5）和（5+1+1）,由于（1+1+5）和上面的（1+1+5）重合，所以算一种切法，依次类推。
由于我们对 n-1个切点总是可以选择切割或不切割，所以长度为 n 的钢条共有 2^(n-1)中不同的切割方案不懂的点我

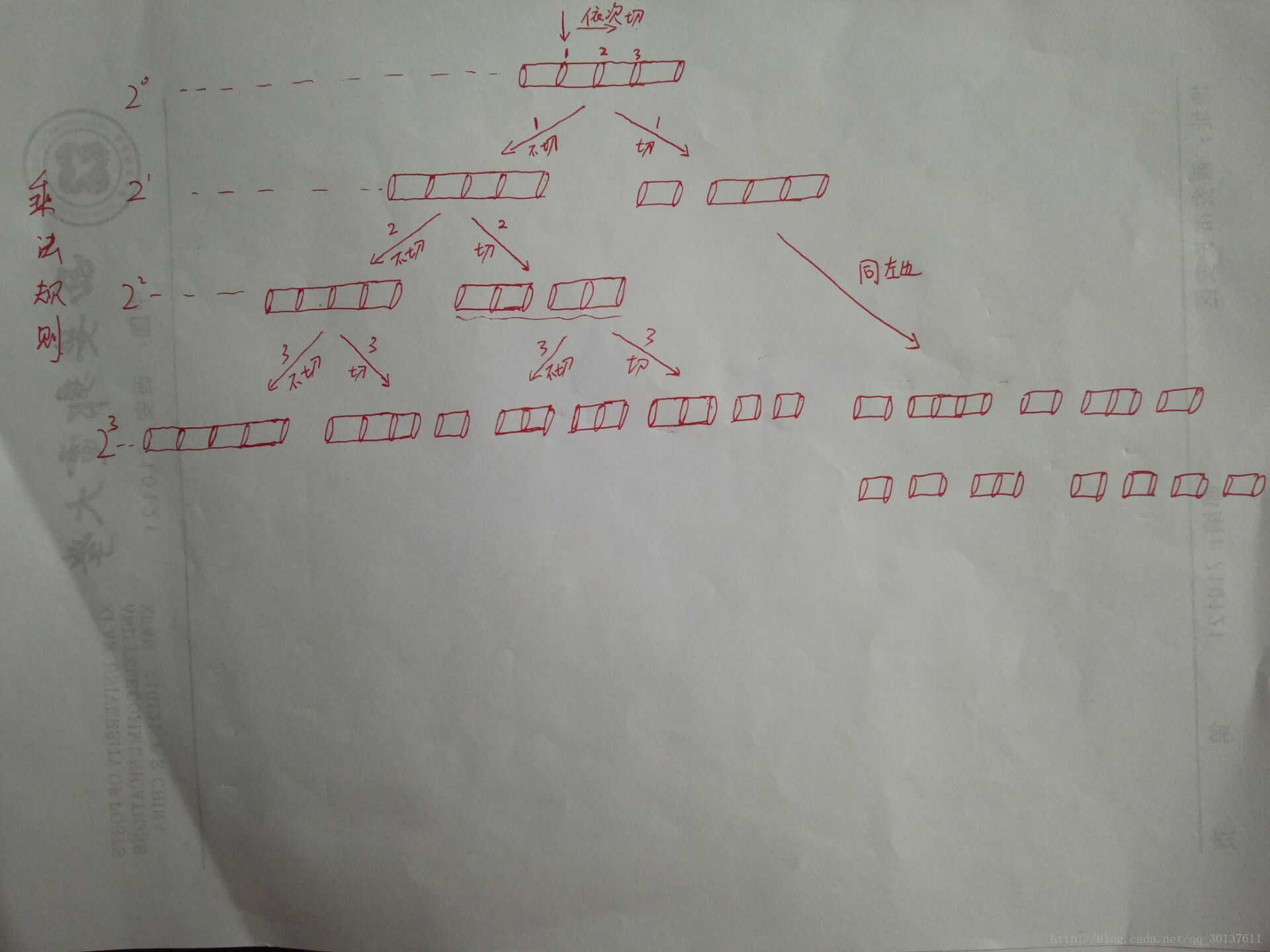
 2>从这2^(n-1)中方案中选出可以获得最大收益的一种方案

学过递归的小王很快就把上述过程抽象成了一个函数，写出了以下的数学表达式：
设钢条长度为n的钢条可以获得的最大收益为 r(n) （n>=1）

第一个参数P(n)表示不切割对应的方案，其他 n-1个参数对应着另外 n-1中方案（对应上面的一刀切）
为了求解规模为 n 的原问题，我们先求解形式完全一样，但规模更小的子问题。即当完成首次切割后，我们将两段钢条看成两个独立的钢条切割问题来对待。我们通过组合两个相关子问题的最优解，并在所有可能的两段切割方案中选取组合收益最大者，构成原问题的最优解我们成钢条问题满足最优子结构性质
编程能力很强的小王拿出笔记本
很快的在电脑上写下了如下代码

#include <stdio.h>

int CUT_ROD(int * p ,int n);
int max(int q, int a);

int main(void){
    int i = 0;
    int p[10] = {1,5,8,9,10,17,17,20,24,30};
    printf("请输入钢条的长度(正整数):
");
    scanf("%d",&i);

    int maxEarning = CUT_ROD(p,i); // 切割钢条
    printf("钢条长度为 %d 的钢条所能获得的最大收益为:%d
",i,maxEarning);

    return 0;
}
// 切割钢条
int CUT_ROD(int * p,int n){
    int i;
    if(n < 0){
        printf("您输入的数据不合法！
");
        return -1;
    }else if(n == 0){
        return 0;
    }else if(n > 10){
        printf("您输入的值过大！
");
        return -1;
    }
    int q = -1;
    for(i = 0; i < n;i++){
        q = max(q,p[i] + CUT_ROD(p,n-1-i));
    }
    return q;
}

int max(int q, int a){
    if(q > a)
        return q;
    return a;
}

 沾沾自喜的小王拿着自己的代码到boss面前，说已经搞定了。boss看了看他的代码，微微一笑，说，你学过指数爆炸没，你算算你的程序的时间复杂度是多少，看看还能不能进行优化？小王一听蒙了，自己这些还没有想过，自己拿着笔和纸算了好大一会，得出了复杂度为T(n) = 2^n,没想到自己写的代码这么烂，规模稍微变大就不行了。boss看了看小王，说：你想想你的代码效率为什么差？小王想了想，说道：“我的函数CUT-ROD反复地利用相同的参数值对自身进行递归调用，它反复求解了相同的子问题了”boss说：“还不错嘛？知道问题出在哪里了，那你怎样解决呢？”小王摇了摇头，boss说：“你应该听过动态规划吧,你可以用数组把你对子问题求解的值存起来，后面如果要求解相同的子问题，直接用之前的值就可以了，动态规划方法是付出额外的内存空间来节省计算时间，是典型的时空权衡”，听到这里小王暗自佩服眼前的boss，姜还是老的辣呀。

boss说完拿起小王的笔记本，写下了如下代码：

// 带备忘的自顶向下法 求解最优钢条切割问题
#include <stdio.h>

int MEMOIZED_CUT_ROD(int * p,int n);
int MEMOIZED_CUT_ROD_AUX(int * p, int n, int * r);
int max(int q,int s);

int main(void){
    int n;
    int p[11]={-1,1,5,8,9,10,17,17,20,24,30};
    printf("请输入钢条的长度（正整数 < 10）:
");
    scanf("%d",&n);
    if(n < 0 || n >10){
        printf("您输入的值有误！");
    }else{
        int r = MEMOIZED_CUT_ROD(p,n);
        printf("长度为%d的钢条所能获得的最大收益为:%d
",n,r);
    }
    return 0;
}

int MEMOIZED_CUT_ROD(int * p, int n){
    int r[20];
    for(int i = 0; i <= n; i++){
        r[i] = -1; 
    }
    return MEMOIZED_CUT_ROD_AUX(p,n,r); 
}

int MEMOIZED_CUT_ROD_AUX(int * p, int n, int * r){
    if(r[n] >= 0){
        return r[n];
    }
    if(n == 0){
        return 0;
    }else{
        int q = -1;
        for(int i = 1; i <= n; i++){// 切割钢条， 大纲有 n 中方案
            q = max(q,p[i] + MEMOIZED_CUT_ROD_AUX(p,n-i,r));  
        }
        r[n] = q;// 备忘
        return q;
    }
}

int max(int q, int s){
    if(q > s){
        return q;
    }
    return s;
}

 小王两眼瞪的直直的。boss好厉害，我这刚入职的小白还得好好修炼呀。

写完boss说：这中方法被称为带备忘的自顶向下法。这个方法按自然的递归形式编写过程，但过程会保存每个子问题的解（通常保存在一个数组或散列表中），当需要一个子问题的解时，过程首先检查是否已经保存过此解，如果是，则直接返回保存的值。还有一种自底向上法。这种方法一般需要恰当定义子问题的规模，使得任何子问题的求解都只依赖于“更小的”子问题的求解。因而我们可以将子问题按规模排序，按由小至大的顺序进行求解，当求解某个子问题是，它所依赖的那些更小的子问题都已经求解完毕，结果已经保存，每个子问题只需求解一次。如果你有兴趣回去好好看看书自己下去好好研究下吧。
最后再考考你，我写的这个带备忘的自顶向下法的时间复杂度是多少？小王看了看代码，又是循环，又是递归的，脑子都转晕了。boss接着说：“你可以这样想，我这个函数是不是对规模为0，1，…，n的问题进行了求解，那么你看，当我求解规模为n的子问题时，for循环是不是迭代了n次，因为在我整个n规模的体系中，每个子问题只求解一次，也就是说我for循环里的递归直接返回的是之前已经计算了的值，比如说 求解 n =3的时候，for(int i = 1,i <=3;i++)，循环体执行三次，n=4时，循环体执行四次，所以说，我这个函数MEMOIZED_CUT_ROD进行的所有递归调用执行此for循环的迭代次数是一个等差数列，其和是O(n^2)”,是不是效率高了许多。小王嗯嗯直点头，想着回去得买本《算法导论》好好看看。

无后效性是一个问题可以用动态规划求解的标志之一，理解无后效性对求解动态规划类题目非常重要

转自：http://blog.csdn.net/qq_30137611/article/details/77655707

---

某阶段的状态一旦确定，则此后过程的演变不再受此前各种状态及决策的影响

百度百科是这样定义的，是不是很苦涩，难懂。并且网上对这个名词的解释大多都是理论性的，不好理解，今天我们通过一个例子来看看什么是无后效性

现在有一个四乘四的网格，左上角有一个棋子，棋子每次只能往下走或者往右走，现在要让棋子走到右下角

假设棋子走到了第二行第三列，记为s(2,3),如下图，画了两条路线和一条不符合题意的路线，那么当前的棋子[s(2,3)位置]怎么走到右下角和之前棋子是如何走到s(2,3)这个位置无关[不管是黑色尖头的路线还是蓝色箭头的路线]

换句话说，当位于s(2,3)的棋子要进行决策（向右或者向下走）的时候，之前棋子是如何走到s(2,3)这个位置的是不会影响我做这个决策的。之前的决策不会影响了未来的决策（之前和未来相对于现在棋子位于s(2,3)的时刻），这就是无后效性,也就是所谓的“未来与过去无关”

看完了无后效性，那我们再来看看有后效性，还是刚才的例子，只不过现在题目的条件变了，现在棋子可以上下左右走但是不能走重复的格子

那么现在红色箭头就是一个合法的路线了，当我的棋子走到了s(2,3)这个位置的时候，要进行下一步的决策的时候，这时候的决策是受之前棋子是如何走到s(2,3)的决策的影响的，比如说红色箭头的路线，如果是红色箭头决策而形成的路线，那么我下一步决策就不能往下走了[因为题意要求不能走重复的格子]，之前的决策影响了未来的决策，”之前影响了未来”,这就叫做有后效性

在此感谢腾讯大神的指导，学习离不开自己的努力和名师的指导。