神经网络-不适合小白

神经网络(手写数字1-10识别)

变量

• 数据中给出的标签y为1-10之间的数字, 但是为了带入分类算法, 将(y)转为(R^{1 imes10})的向量表示1-10之间的数据, 如[0 0 0 0 1 0 0 0 0 0], 则表示5等等
• (K): (y^{(i)})的长度, 这里是10
• (m): 样本的数量
• (n): 特征的数量, 包括偏移+1的特征
• 假设激活函数为sigmoid函数, 即({1over{1+e^{(-x)}}})

公式

损失函数

• (cost(h_Theta(x^{(i)})-y^{(i)}))为

[cost(h_Theta(x^{(i)})-y^{(i)}) = sum_{k=1}^{K} y_k^{(i)}log(h_Theta(y_k^{(i)})) + (1 - y_k^{(i)})log(1 - h_Theta(y_k^{(i)})) ]

• 损失函数(J)为

[J(Theta) = {1over{m}}sum_{i=1}^{m}cost(h_Theta(x^{(i)})-y^{(i)}) + {lambdaover{2m}}sum_{l}^{L-1}sum_{i=1}^{s_l}sum_{j=1}^{s_{l+1}}Theta_{ji}^{l} ]

• 上面式子展开为

[J(Theta) = {1over{m}}sum_{i=1}^{m}sum_{k=1}^{K} y_k^{(i)}log(h_Theta(y_k^{(i)})) + (1 - y_k^{(i)})log(1 - h_Theta(y_k^{(i)})) + {lambdaover{2m}}sum_{l}^{L-1}sum_{i=1}^{s_l}sum_{j=1}^{s_{l+1}}Theta_{ji}^{l} ]

正向传播与反向传播

• 为什么使用正向传播与反向传播
  • 有了正向传播, 计算出输出层的结果, 就可以带入我们上面的公式计算出J
  • 有了正向传播再加上反向传播, 就可以更快的计算出每一个权重的梯度, 而不是向传统方法一样一个一个的给权重求导数
• 可以会误解的
  • 在反向传播中, 第一步就是(h_Theta(x)-y), 对于这个式子可能会有人认为这个就是J, 其实不是, 它与J一点关系都没有, 它仅仅是为了反向传播中计算出各个计算节点的误差值而产生的

神经网络示意图

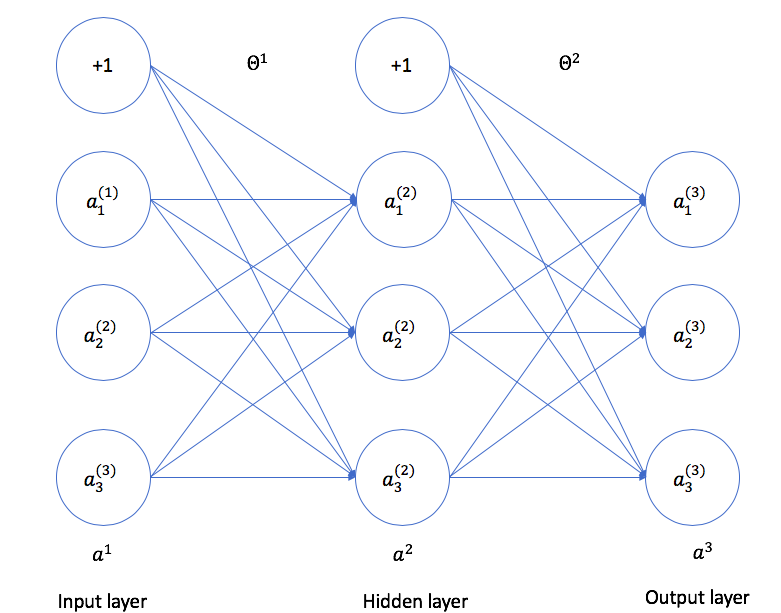
• 在字母右上角的数字表示第几层

• 权重矩阵的维度计算

  • (l): 表示当前层
  • (s_l): 表示当前层有几个节点, 不包括+1偏移节点
  • (s_{l+1} imes(s_l+1))
  • 比如(Theta^{(1)})就是(l=1)时, (size(Theta^{(1)})=3 imes 4)

• (a1)表示一个输入样本, 也就是输入层, (a_1^{(1)},a_2^{(1)}, a_3^{(1)})表示3个特征, 其中+1在第1层表示为(a_0^{(1)}), 在第2层表示为(a_0^{(2)})

• (a^{(2)})表示隐藏层

• (a^{(3)})表示输出层, 可以理解为(h_Theta(x^{(i)}))

• (Theta^{(1)})表示输入层到隐藏层的权重矩阵

• (Theta^{(2)})表示隐藏层到输出层的权重矩阵

• 现在不考虑bias节点, 输入层有3个节点, 隐藏层有3个节点, 输出层有3个节点, 这里只有输入层没有激活函数, 也就是没有运算的功能, 仅仅是担任提供数据的功能, 我们常说一个神经网络是2层, 3层之类的, 是根据该神经网络的计算层的个数判断的, 我们这里的神经网络就是一个2层神经网络

• 根据当前神经网络列出正向传播公式(对于单个样本)

  • 在这之前, 先随机初始化权重矩阵(第1层与第2层的权重矩阵), 如果初始化, 见下文
  • (a^{(1)}=x^{(i)})
  • (a_1^{(2)}=g(Theta_{10}a_0^{(1)}+Theta_{11}a_1^{(1)}+Theta_{12}a_2^{(1)}+Theta_{13}a_3^{(1)})), 其中(g())为sigmoid函数, 括号里面的(Theta_{10}a_0^{(1)}+Theta_{11}a_1^{(1)}+Theta_{12}a_2^{(1)}+Theta_{13}a_3^{(1)})式子因为太长, 一般使(z_1^{(2)}=Theta_{10}a_0^{(1)}+Theta_{11}a_1^{(1)}+Theta_{12}a_2^{(1)}+Theta_{13}a_3^{(1)}), 从而, (a_1^{(2)}=g(z_1^{(2)}))
  • 同理, (a_2^{(2)}=g(Theta_{20}a_0^{(1)}+Theta_{21}a_1^{(1)}+Theta_{22}a_2^{(1)}+Theta_{23}a_3^{(1)})), 所以, (z_2^{(2)}=Theta_{20}a_0^{(1)}+Theta_{21}a_1^{(1)}+Theta_{22}a_2^{(1)}+Theta_{23}a_3^{(1)}), 从而得到, (a_2^{(2)}=g(z_2^{(2)}))
  • (a_3^{(2)}=g(z_2^{(2)}))
  • 到了第2层也是如此
  • 最后计算得出
    • (a_1^{(3)}=g(z_1^{(3)}))
    • (a_2^{(3)}=g(z_2^{(3)}))
    • (a_3^{(3)}=g(z_3^{(3)}))
    • 到此单样本正向传播结束

• 上面的式子, 由于是在一个样本中一个特征一个特征的计算, 所以有一点繁琐, 但是只要理解了每一个特征的计算方法, 那么转为矩阵运算或者向量运算是非常方便的, 接下来就将上面的式子转为向量式

  • (a^{(1)}=x^{(i)})
  • (z^{(2)}=Theta^{(1)}a^{(1)})
  • (a^{(2)}=g(z^{(2)}))
  • (z^{(3)}=Theta^{(2)}a^{(2)})
  • (a^{(3)}=g(z^{(3)}))
  • 到此单样本的正向传播结束

• 上面已经完成了正向传播, 现在进行反向传播

  • 对于单个样本, 列出向量表达式
    • (delta^{(3)}=h_Theta(a^{(3)})-y^{(i)}), 这里的y是已经从1-10的数字转为向量表示的向量
    • (delta^{(2)}=(Theta^{(2)})^{T}delta^{(3)}.*g(z^{(2)}))
    • (Delta^{(2)}=delta^{(2)}(a^{(1)})^{T}), (Delta^{(3)}=delta^{(3)}(a^{(2)})^{T})
    • 现在已经计算完了对于单个样本来说每一个计算节点的误差值
    • 对于剩下的(m-1)个样本, 记录每一个迭代的(delta^{(2)})和(delta^{(3)})的值, 在乘以对应的(a^{(x)}), 将结果分别累加到(Delta^{(2)})和(Delta^{(2)})
    • 接着({1over{m}}Delta^{(2)}+{lambdaover{m}}Theta), 注意偏移的权重不能正则化
  • 最后得到的(Delta^{(2)})和(Delta^{(3)})就是(Theta^{(1)})矩阵和(Theta^{(2)})矩阵的梯度矩阵
  • 注意: 在使用BP求梯度的时候, 一般是一个矩阵一个矩阵的权重去求的, 而传统的梯度是由一个一个的权重去求的, 或者直接通过权重向量去求

随机初始化矩阵

• 公式

[epsilon = 0.12 ]

[W = rand(inputSize, outputSize + 1) imes 2epsilon - epsilon ]

• 为什么这里是inputSize和(outputSize + 1)在上文提到的公式中提到了

梯度检验

• 虽然BP可以快速计算出权重的导数, 但是它复杂, 论准确率, 还是传统求梯度的方法更好, 但就是太慢了, 所以通过使用梯度检验的方式检验我们实现的BP是否正确
• 我们不那训练集, 而是自己常见简单固定的数据, 并且神经网络要简单, 否则速度很慢
• 因为J比较复杂, 所以我们根据梯度的定义去求导
  • (gradOf heta_1={{J( heta_1 + epsilon, heta2, ...) - J( heta_1 - epsilon, heta2, ...)}over{2epsilon}})
  • 一次对所有的( heta)求导, 将他们以一个向量的方式导出

小技巧

• 在将一个向量式子转为一个矩阵式子的时, 可以列出他们的维度, 根据维度判断怎样在矩阵式子中是成立的