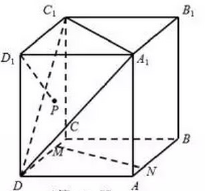
如图.在正方体$ABCD-A_1B_1C_1D_1$中,点$M,N$分别是直线$CD,AB$上的动点,点$P$是$Delta A_1C_1D_1$内的动点(不包括边界),记直线$DP$与$MN$所成角为$ heta$,若$ heta$的最小值为$dfrac{pi}{3}$,则点$P$的轨迹为( )
A.圆的一部分
B.椭圆的一部分
C.抛物线的一部分
D.双曲线的一部分

答案 B
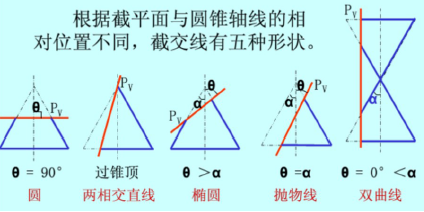
分析:“二面角最大,线面角最小”.从而我们知道$D_1P$与底面$ABCD$所成的角为$dfrac{pi}{3}$,故$P$在以$DD_1$为轴的圆锥面上,所以$P$的轨迹为面$A_1C_1D$截圆锥所得的曲线.
$e=dfrac{cos heta}{cosalpha}=dfrac{dfrac{sqrt{6}}{3}}{cosdfrac{pi}{6}}=dfrac{2sqrt{2}}{3}in(0,1)$ 为椭圆.
(其中$ heta$为截面$A_1C_1D$与圆锥的对称轴$DD_1$的夹角,$alpha$为圆锥母线与圆锥对称轴的夹角)