「算法笔记」二分图匹配

一、相关定义

二分图：如果一个图的顶点能够被分为两个集合 X,Y，满足每一个集合内部都没有边相连，那么这张图被称作是一张二分图。

匹配：在图论中，一个匹配（matching）是一个边的集合，其中任意两条边都没有公共顶点。

最大匹配：一个图所有匹配中，所含匹配边数最多的匹配，称为这个图的最大匹配。

完美匹配：如果一个图的某个匹配中，所有的顶点都是匹配点，那么它就是一个完美匹配。

二、最大匹配——匈牙利算法

1. 基本思想

在进行匈牙利算法之前，我们先做两个比较重要的定义：

交替路：从一个未匹配点出发，依次经过非匹配边、匹配边、非匹配边、……形成的路径叫交替路。（换言之，交替路是图的一条简单路径，满足任意相邻的两条边，一条在匹配内，一条不在匹配内。）

增广路：从一个未匹配点出发，依次经过非匹配边、匹配边、非匹配边、……、非匹配边，最后到达一个未匹配点形成的路径叫增广路。（换句话说，增广路是一个始点与终点都为非匹配边的交错路。）

注意到，一旦我们找出了一条增广路，将这条路径上所有匹配边和非匹配边取反，就可以让匹配边数 +1，即可以得到一个更大的匹配。进一步可以得到推论：二分图的一组匹配 S 是最大匹配，当且仅当图中不存在 S 的增广路。匈牙利算法就是基于这个原理。

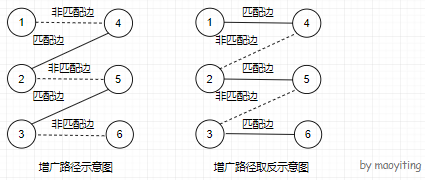
假设我们已经得到了一个匹配，希望找到一个更大的匹配。我们从一个未匹配点出发进行 dfs，如果找出了一个增广路，就代表增广成功，我们找到了一个更大的匹配。如果增广失败，可以证明此时就是最大匹配。

2. 具体实现

匈牙利算法的主要过程：

设 S=∅，即所有边都是非匹配边。
找到一条增广路，把路径上所有边的匹配状态取反，得到一个更大的匹配 S'。
重复第 2 步，直至图中不存在增广路。

该算法的关键在于如何找到一条增广路。具体实现如下：

从二分图的 X 部中取出一个为未匹配的顶点 u 开始，找一个未访问的邻接点 v（v 一定属于 Y 部的顶点）。对于 v，分两种情况：

若 v 是未匹配点，此时无向边 (u,v) 本身就是非匹配边，自己构成一条长度为 1 的增广路。
若 v 是已匹配点，则取出 v 的匹配顶点 w（w 一定是 X 部的顶点），边 (w,v) 目前是匹配边，根据“取反”的想法，要将 (w,v) 改为未匹配，(u,v) 改为匹配，条件为以 w 为起点可以新找到一条增广路径 P'，那么 u→v→P' 就是一条以 u 为起点的增广路径。

代码片段：

bool find(int x){     //mp 存储匹配边 
    for(int i=hd[x];i;i=nxt[i]){
        int y=to[i];
        if(vis[y]) continue;    //如果访问过就跳过 
        vis[y]=1;    //打上访问标记 
        if(!mp[y]||find(mp[y])){mp[y]=x;return 1;}    //如果 v 是非匹配边或从 v 出发能够找到增广路，则设置为匹配边 
    }
    return 0;    //找不到增广路了，返回 0 
}

匈牙利算法模板题：HDU 2063 过山车（求二分图的最大匹配数）

#include<bits/stdc++.h>
#define int long long
#define MEM(x,y) memset(x,y,sizeof(x))
using namespace std;
const int N=1e3+5;
int k,n,m,x,y,cnt,hd[N],to[N<<1],nxt[N<<1],mp[N],ans;
bool vis[N];
void add(int x,int y){
    to[++cnt]=y,nxt[cnt]=hd[x],hd[x]=cnt;
}
bool find(int x){
    for(int i=hd[x];i;i=nxt[i]){
        int y=to[i];
        if(vis[y]) continue;
        vis[y]=1;
        if(!mp[y]||find(mp[y])){mp[y]=x;return 1;}
    }
    return 0;
} 
signed main(){
    while(~scanf("%lld",&k)&&k){
        scanf("%lld%lld",&n,&m),cnt=0,ans=0,MEM(hd,0),MEM(mp,0);
        for(int i=1;i<=k;i++)
            scanf("%lld%lld",&x,&y),add(x,y);
        for(int i=1;i<=n;i++){
            MEM(vis,0);
            if(find(i)) ans++;
        }
        printf("%lld
",ans);
    }
    return 0;
}

三、二分图最大权匹配——KM 算法

现在我们把所有的边都带上权值，希望求出所有最大匹配中权值之和最大的匹配。

我们的思路是给每一个点赋一个“期望值”，也叫作顶标函数 c，对于边 (u,v)，只有 c(u)+c(v)=w(u,v) 的时候，才能被使用。

容易发现，此时的答案就是 c(i) 之和。

初始，我们令左边所有点的 c(u)=max_v w(u,v)，也就是说最理想的情况下，每一个点都被权值最大的出边匹配。

接下来开始增广，每次只找符合要求的边。我们定义只走这些边访问到的子图为相等子图。

如果能够找到增广路就直接增广，否则，就把这次增广访问到的左边的所有点的 c-1，右边所有点的 c+1。

经过这样一通操作，我们发现原来的匹配每一条边仍然满足条件。同时由于访问到的点左边比右边多一个（其余的都匹配上了），所以这样会导致总的权值 -1。

接下来再尝试进行增广，重复上述过程。直接这样做时间复杂度是 O(n³c) 的。（进行 n 次增广，每次修改 c 次顶标，访问所有 n² 条边）

一些优化：

由于修改顶标的目标是让相等子图变大，因此可以每次加减一个最小差值 delta。这样每次增广只会被修改最多 n 次顶标，时间复杂度降到 O(n⁴)。
注意到每次重新进行 dfs 太不优秀了，可以直接进行 bfs，每次修改完顶标之后接着上一次做。时间复杂度降到 O(n³)。

四、一般图的情况？

一般图最大匹配？O(n³) 带花树。然鹅我不会。

一般图最大权匹配？带权带花树？显然我也不会。

五、二分图的覆盖与独立集

1. 二分图的最小点覆盖

最小点覆盖：选取最少的点，使得每一条边的两端至少有一个点被选中（也就是，“点”覆盖了所有的“边”）。

二分图的最小点覆盖=最大匹配。具体地说，二分图最小点覆盖包含的点数等于二分图最大匹配包含的边数。

证明：

由于最大匹配中的边必须被覆盖，因此匹配中的每一个点对中都至少有一个被选中。
选中这些点后，如果还有边没有被覆盖，则找到一条增广路，矛盾。

2. 二分图的最大独立集

最大独立集：选取最多的点，使得任意两个点不相邻。其中，选取最多的点的点集被称作最大独立集。

最大独立集=点数-最小点覆盖。（又因为二分图的最小点覆盖=最大匹配，所以最大独立集=点数-最大匹配）

证明：

由于最小点覆盖覆盖了所有边，因此选取剩余的点一定是一个合法的独立集。
若存在更大的独立集，则取补集后得到了一个更小的点覆盖，矛盾。

3. 二分图的最小边覆盖

最小边覆盖：选取最少的边，使得每一个点都被覆盖。

最小边覆盖=点数-最大匹配。

证明：

先选取所有的匹配边，然后对剩下的每一个点都选择一条和它相连的边，可以得到一个边覆盖。
若存在更小的边覆盖，则因为连通块数量=点数-边数，这个边覆盖在原图上形成了更多的连通块，每一个连通块内选一条边，我们就得到了一个更大的匹配。

4. 二分图的路径覆盖

最小不相交路径覆盖：一张有向图，用最少的链覆盖所有的点，链之间不能有公共点。

将点和边分别作为二分图的两边，然后跑匹配，最小链覆盖=原图点数-最大匹配。

最小可相交路径覆盖：一张有向图，用最少的链覆盖所有的点，链之间可以有公共点。

先跑一遍 Floyd 传递闭包，然后变成最小不相交路径覆盖。

六、二分图的应用

1.「ZJOI 2007」矩阵游戏

题目大意：给一个 n×n 的黑白方阵，你可以任意交换两行或者两列。求是否能够让主对角线上都是黑色。n≤200，多测最多 20 组。

Solution：

假设我们选出了 n 个点的坐标。如果这 n 个点所在的行、列互不相同，那么一定可以通过交换来完成任务。（考虑到两个同行的格子不可能最终到不同行上，列也一样。最终我们要让主对角线上都是黑色，也就是说，我们要让每行每列都有黑色。所以我们最终找到的 n 个点必然在一开始横纵坐标就互不相同。）

转化为二分图匹配。建一个二分图，左边是行，右边是列。如果 (i,j) 是黑色就从 i 到 j 连边。

最后看是否存在完美匹配。可以用匈牙利算法解决。

#include<bits/stdc++.h>
#define int long long
#define MEM(x,y) memset(x,y,sizeof(x))
using namespace std;
const int N=1e5+5;
int t,n,x,cnt,hd[N],to[N<<1],nxt[N<<1],mp[N],ans;
bool vis[N];
void add(int x,int y){
    to[++cnt]=y,nxt[cnt]=hd[x],hd[x]=cnt;
}
bool find(int x){
    for(int i=hd[x];i;i=nxt[i]){
        int y=to[i];
        if(vis[y]) continue;
        vis[y]=1;
        if(!mp[y]||find(mp[y])){mp[y]=x;return 1;}
    }
    return 0;
} 
signed main(){
    scanf("%lld",&t);
    while(t--){
        scanf("%lld",&n),cnt=0,ans=0,MEM(hd,0),MEM(mp,0);
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++){
                scanf("%lld",&x);
                if(x) add(i,j);    //如果 (i,j) 是黑色就从 i 到 j 连边
            }
        for(int i=1;i<=n;i++){
            MEM(vis,0);
            if(find(i)) ans++;
        }
        puts(ans==n?"Yes":"No");
    }
    return 0;
}

2. POJ 2446 Chessboard

题目大意：一个 n×m 的网格，其中有若干个位置被删掉了。你需要用 1×2 的骨牌覆盖其余所有的位置，判断是否可行。1≤n,m≤32。

Solution：

将整个棋盘进行黑白染色，则一个骨牌一定覆盖了相邻两个颜色不同的位置。

相邻位置连边，然后跑二分图匹配，如果存在完美匹配那就可以，否则不行。

#include<cstdio>
#include<cstring>
#define MEM(x,y) memset(x,y,sizeof(x))
using namespace std;
const int N=40,M=1e5+5;
int n,m,K,x,y,mp[M],cnt,hd[M],to[M<<1],nxt[M<<1],ans,dx[4]={1,-1,0,0},dy[4]={0,0,1,-1};
bool a[N][N],vis[M];
void add(int x,int y){
    to[++cnt]=y,nxt[cnt]=hd[x],hd[x]=cnt;
}
bool find(int x){
    for(int i=hd[x];i;i=nxt[i]){
        int y=to[i];
        if(vis[y]) continue;
        vis[y]=1;
        if(!mp[y]||find(mp[y])){mp[y]=x;return 1;}
    }
    return 0;
} 
signed main(){
    while(~scanf("%d%d%d",&n,&m,&K)){
        cnt=ans=0,MEM(hd,0),MEM(a,0),MEM(mp,0);
        for(int i=1;i<=K;i++)
            scanf("%d%d",&y,&x),a[x][y]=1;    //标记被删掉的位置 
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++){
                if(a[i][j]||(i+j)&1) continue;
                for(int k=0;k<4;k++){
                    x=i+dx[k],y=j+dy[k];
                    if(a[x][y]||x<1||x>n||y<1||y>m) continue;
                    add(i*m+j,x*m+y);    //相邻位置连边 
                }
            }
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++){
                if(a[i][j]||(i+j)&1) continue;
                MEM(vis,0);
                if(find(i*m+j)) ans++;
            }
        puts(2*ans==n*m-K?"YES":"NO"); 
    }
    return 0;
}

3. ZOJ 3988 Prime Set

题目大意：给定 n 个整数 a₁,...,a_n，你需要从中选出 k 个数对 {a_x1,a_y1 },{a_x2,a_y2 },..., {a_xk,a_yk}（数对之间可以有重复元素），使得每一对数对的和都是质数。
你需要最大化这 k 个数对求并后集合里的元素个数。 1≤n≤3×10³，1≤k≤n(n-1)/2。

Solution：

首先跑素数筛，得出所有可以形成质数的数对。

先忽略 1+1=2 的情况，那么所有合法的数对一定奇偶不同（除了 2 外的质数都是奇数，奇数+偶数=奇数）。

建一个二分图，左边是奇数，右边是偶数。跑一遍最大匹配，然后再把 1+1=2 的情况考虑进去，剩下的贪心选取。

注意 1 的位置需要特殊处理。

#include<bits/stdc++.h>
#define int long long
#define MEM(x,y) memset(x,y,sizeof(x)) 
using namespace std;
const int N=3e3+5,M=2e6+5;
int t,n,k,a[N],p[M],cnt,hd[M],to[M<<1],nxt[M<<1],mp[M],ans,sum,tmp;
bool vis[M],v[M];
void add(int x,int y){
    to[++cnt]=y,nxt[cnt]=hd[x],hd[x]=cnt;
}
bool find(int x){
    for(int i=hd[x];i;i=nxt[i]){
        int y=to[i];
        if(vis[y]) continue;
        vis[y]=1;
        if(mp[y]==-1||find(mp[y])){mp[x]=y,mp[y]=x;return 1;}
    }
    return 0;
} 
signed main(){
    vis[0]=vis[1]=1;
    for(int i=1;i<=2e6;i++){    //线性筛 
        if(!vis[i]) p[++cnt]=i,v[i]=1;
        for(int j=1;j<=cnt&&i*p[j]<=2e6;j++){
            vis[i*p[j]]=1;
            if(i%p[j]==0) break;
        }
    } 
    scanf("%lld",&t);
    while(t--){
        scanf("%lld%lld",&n,&k),cnt=ans=sum=tmp=0,MEM(hd,0);
        for(int i=1;i<=n;i++)
            scanf("%lld",&a[i]),mp[i]=-2;
        for(int i=1;i<=n;i++)    //建二分图 
            for(int j=i+1;j<=n;j++)
                if(v[a[i]+a[j]]){ 
                    mp[i]=mp[j]=-1;
                    if(a[i]==1&&a[j]==1) continue;
                    a[i]&1?add(i,j):add(j,i);
                } 
        for(int i=1;i<=n;i++)
            if(mp[i]==-1&&(a[i]&1)) MEM(vis,0),ans+=find(i);
        for(int i=1;i<=n;i++){
            if(mp[i]<0&&a[i]==1) sum++;     //特殊处理 1+1=2 的情况 
            if(mp[i]==-2) tmp++;
        } 
        ans+=sum/2,tmp=n-tmp-ans*2;    //ans:数对个数  tmp:剩余的未被匹配的元素个数 
        if(ans>=k) printf("%lld
",k*2);    //至多选出 k 个两两不相交的集合，每个集合有 2 个元素，所以答案为 2*k 
        else printf("%lld
",2*ans+min(tmp,k-ans));    //若 i 未被匹配，表示 (i,j) 中 j 已匹配其他元素，故若选择 (i,j) 只会得到 1 个不同元素 i，所以答案为 2*ans+min(tmp,k-ans)。 
    }
    return 0;
}