一、概述
在前一篇中我们回顾了红黑树的特点及添加的处理,可以得知红黑树首先是一个二叉查找树,在此基础上通过增加节点颜色的约束来使得红黑树近似平衡。当我们添加或者删除节点时,我们需要对树进行调整以使其重新满足红黑树。这涉及到节点颜色的变化及部分节点的旋转。关于节点的旋转,以及添加时的处理我们已经介绍完了,所以本文重点介绍红黑树的删除。
二、红黑树的特点
在介绍删除时,我们还是再来回顾一下红黑树的五个特点,如下:
1)节点的颜色是红色或者黑色
2)树的根节点为黑色
3)树的叶子节点为黑色
4)如果一个节点的颜色为红色,则其两个儿子节点必为黑色
5)任一节点的两个子树,各路径中的黑色节点的个数相等。
对节点的删除后,这5个性质可能会被破坏,所以删除之后,也需要通过一系列的处理来使整个树重新变为红黑树。
三、红黑树的删除过程
红黑树的删除算法主要有三个步骤
3.1 找到待删除的节点,这是一个二叉查找树的查找过程,比较简单。
3.2 在找到该节点的情况下,根据该节点孩子的情况,又可以分成三种情况:
1) 该节点有两个非叶子节点的孩子
2)该节点有一个非叶子节点的孩子
3)该节点只有叶子节点
在这里,我们所说的叶子节点指的是空节点。那么根据这三种情况,我们需要做不同的处理。
针对于情况1,我们需要找到当前节点的后继节点,后继节点的定义是该节点的子树中,第一个没有左孩子(或左孩子为叶子节点)的节点。找到该节点后,我们需要把该节点的值同步给当前节点,并转而去删除其后继节点。
这样做的好处就是,其后继节点最多只可能有一个孩子(而且是右孩子)。因为根据后继节点的定义,其左孩子必为叶子节点。那这样对于其后续节点再做删除处理的话,就不会有情况1的存在了,而只会有情况2和3的存在。
我们通过示意图来演示如下:
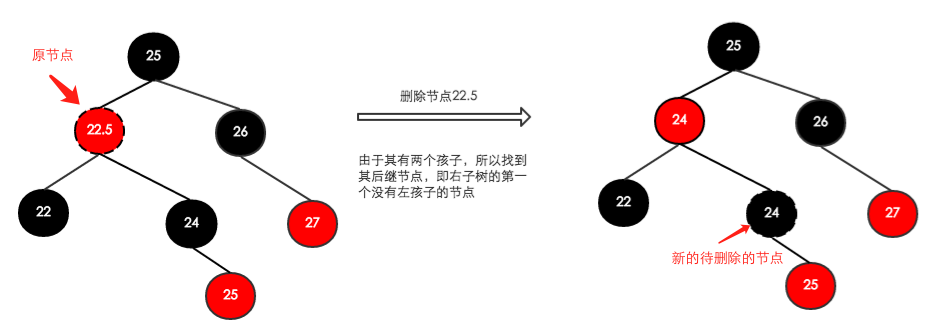
通过上面的处理,我们将删除改为对节点24的删除,但24删除之后其数据就没有了,所以我们把其内容放到原来待删除的节点,22.5上。
针对于情况2,被删除的节点有一个孩子,我们需要找到其惟一的儿子,并将被删除的节点从树中移除,并将这个惟一的儿子作为待处理的起始点,进行树调整。
示意图如下:

针对于情况3,我们直接把当前节点作为起始点进行树的红黑性质调整,只是调整结束后,由于之前并未进行节点的删除,所以需要将当前节点再删除掉。
3.3 对删除节点后树进行调整
在删除节点之后,树的红黑性质可能会被破坏,当被破坏后我们需要对树进行调整。所以,我们要先明确,删除一个节点之后,红黑树的哪些性质可能会被破坏。
a) 当被删除的节点是红色时,比如上图中的27,这个时候其所在的路径中的黑节点个数不会发生变化,即性质5不会被破坏;由于其是红节点,所以其父亲一定是黑色,所以也不会出现父子都为红色的情况,所以性质4不会被破坏;另外红节点一定不是根节点,所以性质2也不会被破坏;另外性质1和性质3不可能被改变。
所以,当删除一个红节点,树的5个性质都不会发生变化,这个树仍然是一个红黑树,不需要做任何处理。
b) 当被删除的节点是黑色的,那么可能出现以下一些情况。
b1)当被删除的是根节点时,且根节点只有一个红儿子,则删除后该节点的红儿子成为了树中的惟一节点,且为红色,这就破坏了性质2。
b2)当被删除的是非根节点,则该节点一定有兄弟节点,要不然因为该节点所在的路径的黑节点个数就比另一个分支多一个了。那正是因为这样的原因,如果该节点被删除,则该节点所在分支的黑节点个数就比其兄弟节点所在的路径的黑节点个数少1个了。所以非根节点的情况下,性质5肯定会被破坏。
b3)当被删除的是非根节点,且父子都为红节点的情况下,当前节点删除后,该节点的孩子成为了该节点的父节点的孩子。如上图所求的节点24和25.
由于会出现这三种情况,所以当被删除的节点是黑色时,我们需要对树的红黑性进行恢复。我们把上面的情况分为两部分,即被删除的节点是不是根,这样来分开处理。如果是根就比较好处理,这种情况下,如果有红儿子则把红儿子变成黑色就结束了,没有红儿子则什么都不用做。
那么对于非根的情况就比较复杂了,前面说过,这种情况下,有两个推论,就是黑节点的个数比其它路径少1,且该节点一定有兄弟节点。我们调整也可以基于这个前提来做。红黑树的提出者给出了一种算法,这个算法接收一个节点作为调整的起始节点,前面说了,这个节点可能是被删除节点的子节点,也可能是被删除节点本身(在没有儿子节点的情况下)。
为了便于循环处理,算法假定当前输入的节点所在的子树是满足红黑树的,但我们知道其实输入节点所在路径的黑节点个数比其它路径少1个,为了解决这个问题,算法假定当前节点具备特殊性,该节点与其它普通的节点相比,多了一重“黑色”,则该节点可能是“黑黑”或者“红黑”,这样就抹平了黑节点少1的问题。但是这种假设只是为了便于我们理解,并不是真正的有这个颜色,在这个假定条件下,我们可以做出一些调整使得整个树满足红黑性,并把缺少的这一重黑色给补回来。
基于这个前提,算法对可能出现的几种情况给出了处理方案。
[1]. 输入节点为红色,兄弟节点颜色任意
这个比较简单,直接把节点变成黑色即可,如下所求:
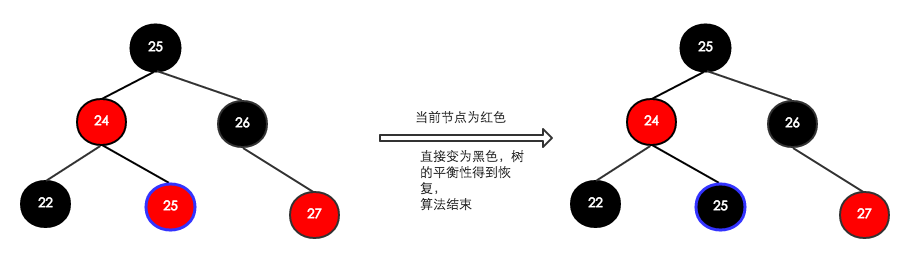
[2] 输入节点为黑色
[2.1] 兄弟节点为红色
这种情况下,很显然,兄弟的父亲和儿子都是黑色的。这个时候我们要想办法把兄弟节点变为黑色,比较好的方案就是在父节点进行左旋,这样原兄弟节点的左孩子就成了父亲节点的右孩子,也就是该节点的兄弟,实现了兄弟节点从红节点到黑节点的转化。
在旋转前,需要将兄弟节点变为黑色,原父亲节点变为红色,才能保持黑节点个数不变。示例如下:
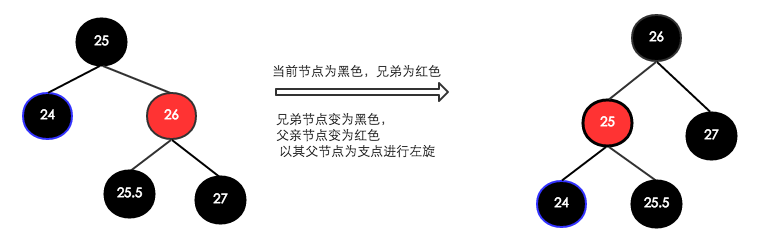
转化完成之后,则兄弟节点变成了黑色,当前节点位置不变,继续处理。
[2.2] 兄弟节点为黑色
[2.2.1] 兄弟节点的两个儿子都是黑色
这种情况下,由于兄弟的两个儿子都为黑色,所以我们有机会把兄弟设置为红色,并将当前节点设置为父亲节点,继续算法。这样,父节点就具备了这个神奇的特性,由于它多了一重黑色,所以虽然兄弟变红了,但兄弟分支上的黑节点个数不变,由于原输入节点已不再是特殊节点,所以原输入节点也就失去了原来多的那一重黑色,所以原输入节点所在的路径黑节点个数也保持不变,说明了这种处理不会影响红黑树的性质。但是我们把当前节点已经提升到了父节点,如果一直是这样的情况,则一定能到根节点以结束。
这个过程的图示如下:

如上图所示,如果[2.1.1]是由[2.1]通过旋转转换而来的话,则当前节点就变成了红色节点,下一次处理时直接将其变红即可。
如果两个儿子不都是黑色,则兄弟节点的孩子中必有一个是红色。在上图中,为了达到抹去节点24中的额外的一重黑色,我们要在保持父节点颜色不变的基础上,为其增加一个黑色节点,要做到这一点,必须以父节点为支点进行左旋转,这样节点24就会下降一级,其所在的路径上便会新增一个节点。由于左旋,且需要人为新增一个黑节点,必然导致原兄弟节点的路径上颜色也发生变化,为了便于着色,我们需要兄弟节点的右孩子为红色。
如果兄弟节点的右孩子本身就为红色,当然直接处理即可,如果右孩子为黑色,则左孩子必为红色,对这种情况,我们需要多做一次旋转。
[2.2.2] 兄弟节点的左孩子是红色,右孩子是黑色
这种情况下,根据前面的分析,我们要做一次旋转让右孩子为红色,这个也比较简单,操作如下:
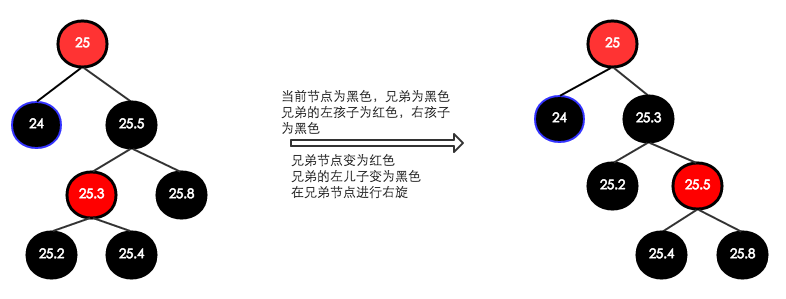
这样就顺利地完成了兄弟节点的左孩子为红色变为右孩子为红色的过程。当右孩子为红色时,就可以进行上面讨论的处理了。
[2.2.3] 兄弟节点的右孩子为红色,左孩子颜色任意
这种情况下,前面说过我们要想办法给当前节点所在的路径增加一个黑色节点,所以要将父节点左旋,同时改变一些节点的颜色,具体操作为:
将父节点变为黑色(此即为新增的节点)
将兄弟节点的颜色变为父节点的颜色(父节点左旋时,兄弟节点要上移成为新的父亲节点,所以它要继承原父亲节点的颜色),以弥补父节点下移的问题
兄弟节点的右儿子颜色变为兄弟节点的颜色(兄弟节点为黑色,所以右儿子自然也为黑色),以弥补兄弟节点颜色丢失的问题。
具体图示如下:

通过以上的处理,我们会发现除了当前节点24所在的路径的黑节点个数增加了之外,其它路径的黑节点个数仍然保持了一致,这样就可以将当前节点的
额外的一重黑色去掉,整个树就重新保持红黑树性质了。
至此,整个删除后节点的调整就到此结束了。
四、代码示例
这里给出TreeMap里关于节点的删除处理。
4.1 删除节点
本部分是删除节点的方法,不包括调整,如下:
private void deleteEntry(Entry<K,V> p) { modCount++; size--; // If strictly internal, copy successor's element to p and then make p // point to successor. if (p.left != null && p.right != null) { //这种情况下找后继节点, Entry<K,V> s = successor(p); //存储后继节点的值 p.key = s.key; p.value = s.value; //P指针指向后继节点,转为对后继节点进行删除 p = s; } // p has 2 children // Start fixup at replacement node, if it exists. //后继节点的儿子节点,只可能有一个 Entry<K,V> replacement = (p.left != null ? p.left : p.right); //因为p只有一个孩子,所以不用两个都处理 if (replacement != null) { //有孩子,则删除节点 replacement.parent = p.parent; if (p.parent == null) root = replacement; else if (p == p.parent.left) p.parent.left = replacement; else p.parent.right = replacement; p.left = p.right = p.parent = null; //如果移除的是红节点则无所谓,不用处理,如果是黑节点则要处理 if (p.color == BLACK) fixAfterDeletion(replacement); //从被删除的儿子节点开始调整 } else if (p.parent == null) { // return if we are the only node. root = null;//删除了根节点 } else { // No children. Use self as phantom replacement and unlink. // 即没有左节点也没有右节点, 则自身作为参数节点 if (p.color == BLACK) fixAfterDeletion(p); //删除自身 if (p.parent != null) { if (p == p.parent.left) p.parent.left = null; else if (p == p.parent.right) p.parent.right = null; p.parent = null; } } }
4.2 具体的调整操作
1 /** From CLR */ 2 private void fixAfterDeletion(Entry<K,V> x) { 3 while (x != root && colorOf(x) == BLACK) { 4 if (x == leftOf(parentOf(x))) { 5 //X为左孩子 6 //兄弟节点 7 Entry<K,V> sib = rightOf(parentOf(x)); 8 9 //2.1 兄弟节点为红色,则通过调整,把兄弟节点变黑 10 if (colorOf(sib) == RED) { 11 12 setColor(sib, BLACK);//兄弟节点变黑色 13 setColor(parentOf(x), RED); //父节点变红 14 rotateLeft(parentOf(x)); //右旋转 15 sib = rightOf(parentOf(x)); //重新定义兄弟节点 16 } 17 18 //2.2 兄弟节点为黑色 19 if (colorOf(leftOf(sib)) == BLACK && 20 colorOf(rightOf(sib)) == BLACK) { 21 //2.2.1 兄弟节点的两个儿子都为黑色 22 setColor(sib, RED); //兄弟节点变红 23 x = parentOf(x); //当前节点上移 24 } else { 25 26 if (colorOf(rightOf(sib)) == BLACK) { 27 //2.2.2 兄弟节点的右孩子为黑色,则要将其调整为红色 28 setColor(leftOf(sib), BLACK); //左孩子设置为黑色 29 setColor(sib, RED); //兄弟节点设置为红色 30 rotateRight(sib); //对兄弟节点右旋 31 sib = rightOf(parentOf(x)); //重新定义兄弟节点 32 } 33 34 //2.2.3 兄弟节点的右孩子为红色 35 setColor(sib, colorOf(parentOf(x)));//兄弟节点的颜色变为其父亲的颜色 36 setColor(parentOf(x), BLACK); //父亲节点的颜色变为黑色 37 setColor(rightOf(sib), BLACK); //兄弟节点的右儿子变为黑色 38 rotateLeft(parentOf(x)); //在父节点进行左旋 39 x = root; //整个树已经恢复为红黑树,x = root,结束循环。 40 } 41 } else { 42 // 对称的操作 43 Entry<K,V> sib = leftOf(parentOf(x)); 44 45 if (colorOf(sib) == RED) { 46 setColor(sib, BLACK); 47 setColor(parentOf(x), RED); 48 rotateRight(parentOf(x)); 49 sib = leftOf(parentOf(x)); 50 } 51 52 if (colorOf(rightOf(sib)) == BLACK && 53 colorOf(leftOf(sib)) == BLACK) { 54 setColor(sib, RED); 55 x = parentOf(x); 56 } else { 57 if (colorOf(leftOf(sib)) == BLACK) { 58 setColor(rightOf(sib), BLACK); 59 setColor(sib, RED); 60 rotateLeft(sib); 61 sib = leftOf(parentOf(x)); 62 } 63 setColor(sib, colorOf(parentOf(x))); 64 setColor(parentOf(x), BLACK); 65 setColor(leftOf(sib), BLACK); 66 rotateRight(parentOf(x)); 67 x = root; 68 } 69 } 70 } 71 72 setColor(x, BLACK); //X一定要置黑,因为X可能是红节点,也可能是ROOT 73 }
上面的代码也完整的介绍了前面介绍的删除操作的对应逻辑,如果前面的图理解了,相信代码也非常容易理解。
五、总结
至此,红黑树的删除就介绍完了,相对于添加来说,这个相对更复杂一些。但只要掌握了其核心思想,以及对于左右旋的操作非常熟悉,也还是能够理解的。再次总结一下删除的主要思想:
1. 首先要确定当前节点是否有两个孩子,有的话,需要找到其直接后继,该后继一定只有不超过一个孩子节点,转而删除其后继
2. 从被删除的节点的儿子节点开始进行删除修复,当该儿子节点为红色时,直接变黑即可,如果为黑色,则需要结合其兄弟节点的颜色一起进行分析。
3. 如果兄弟节点的颜色为红色,则需要将兄弟节点的颜色变为黑色,并对树进行旋转调整。
4. 如果兄弟节点的颜色为黑色,则再针对其儿子节点的颜色情况进行处理
4.1 如果两个儿子都为黑色,则兄弟变为黑色,当前节点指向父亲节点
4.2 如果右儿子为黑色,则需要通过调整将右儿子变为红色
4.3 如果右儿子为红色,则通过一些节点的颜色调整,并在父节点的左旋来完成操作。
最近这两篇文章写了很长时间,不过通过写这个,也算是基本上掌握了红黑树的主要原因和操作,同时也觉得红黑树也并不是那么难以掌握,希望通过这种方式,掌握更多的常用算法。