说到进制转换,java已经封装了基本的方法,在竞赛中使用封装的方法自然能节省大量时间
另一位仁兄介绍的封装好的方法:
https://blog.csdn.net/m0_37961948/article/details/80438113
如果不想看上面的全部,我总结了两条基本方放,记下就可以随意转化:
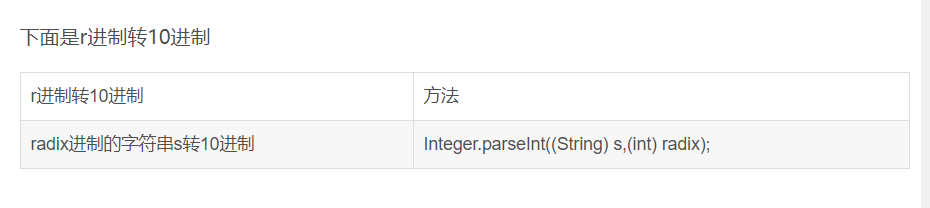

掌握这两个方法就可以实现任意进制的随便转化
(这个是针对竞赛,如果是需要学习底层,大家还在看api研究吧)
再看一个水题:
题目描述
写出一个程序,接受一个十六进制的数值字符串,输出该数值的十进制字符串。(多组同时输入 )
输入描述:
输入一个十六进制的数值字符串。
输出描述:
输出该数值的十进制字符串。
示例1
输入
0xA
输出
10
由于本题目简单,所以只给出代码:
1 import java.util.Scanner; 2 import java.util.*; 3 4 public class Main{ 5 public static void main(String args[]){ 6 Scanner in = new Scanner(System.in); 7 while (in.hasNext()) { 8 String a=in.next(); 9 char[] p=a.toCharArray(); 10 a=String.valueOf(Arrays.copyOfRange(p,2,p.length)); 11 System.out.println(Integer.parseInt(a, 16)); 12 } 13 } 14 }
后面就是靠栈实现任意进制不使用已经封装好的方法:(栈使用的是我自己写的)
1 /** 2 * 进制转换 3 * 算法设计:先将其他进制统一转为10进制,再利用取余法 4 * 将10进制转为其他进制 5 * @param n 需要转化的数 6 * @param n1 需要转化数的进制 7 * @param n2 转化后的进制 8 * @return 转换后的数 9 */ 10 static String systemTransformation(String n, int n1, int n2) { 11 MyArraysStack<Character> e=new MyArraysStack<Character>(); 12 char[] a=new char[]{'0','1','2','3','4','5','6','7','8','9','A','B','C','D','E','F'}; 13 char[] b=n.toCharArray(); 14 int bNumber=0,t=0; 15 //[start]将n1进制转为10进制 16 for (char p:b){ 17 e.push(p); 18 } 19 while (!e.isEmpty()){ 20 char temp=e.pop(); 21 bNumber+= Arrays.binarySearch(a,temp)*Math.pow(n1,t); 22 t++; 23 } 24 //[end] 25 //[start] 将10进制转为n2进制 26 StringBuilder builder=new StringBuilder(); 27 while (bNumber>0){ 28 e.push(a[bNumber%n2]); 29 bNumber/=n2; 30 } 31 while (!e.isEmpty()) { 32 builder.append(e.pop()); 33 } 34 //[end] 35 String str; 36 str=builder.toString(); 37 return str; 38 }
* 算法设计:先将其他进制统一转为10进制,再利用取余法
* 将10进制转为其他进制
* 最高到16进制向其他任意一进制转化
* 如果需要更大的进制则需要扩充a数组即可
当你觉得自己在进制转换上已经完全ok了,此时我又遇到了一道有趣的题目:
题目描述
输入两个整数,求两个整数二进制格式有多少个位不同
输入描述:
两个整数
输出描述:
二进制不同位的个数
示例1
输入
22 33
输出
5
一看到这道题我首先想到,先将两个数转为二进制,然后循环比对出值(突然感到十分麻烦)
然后一看讨论发现了骚操作:
使用异或:
1 public class Solution { 2 /** 3 * 获得两个整形二进制表达位数不同的数量 4 * 5 * @param m 整数m 6 * @param n 整数n 7 * @return 整型 8 */ 9 public int countBitDiff(int m, int n) { 10 String str=Integer.toBinaryString(m^n); 11 str=str.replaceAll("0",""); 12 return str.length(); 13 } 14 }
异或就是不同为1,相同为0,将m和n异或,是位运算,m^n的结果是m和n二进制的异或结果
Integer.toBinaryString();将m^n转为二进制
然后替换了字符串里面的0,返回字符串长度,即得到了不同的位数