写在最前
对于形如(z=f(x,y))的函数,求解极值的通法一般有两种:
- 偏导数法
- 二元全微分法
由于偏导数法操作简单,下面仅介绍这种方法
二元函数极值点
(Ops:)只想知道最值的可以跳过这一节。
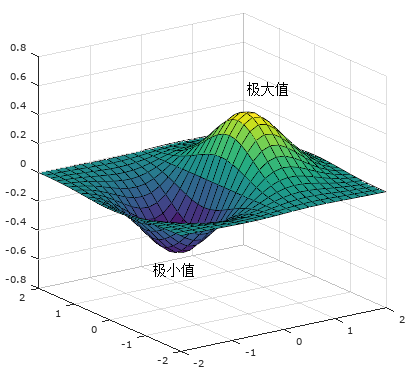
我们以驻点为圆心在(xy)平面上做一个圆(就如同在一元函数(y=f(x))驻点附近找一段区间),若当半径足够小时,(f(x_0,y_0))是该圆形区域的最大值或最小值, 那么该驻点就是极大值点或极小值点。与一元函数类似,驻点不一点是极值点。
那么我们如何判断极点呢?
一个比较常规的想法是,让(f_x)在(x=x_0)的两边异号,让(f_y)在(y=y_0)的两边异号,借此来判断函数的极值点。但有一个很明显的错误:
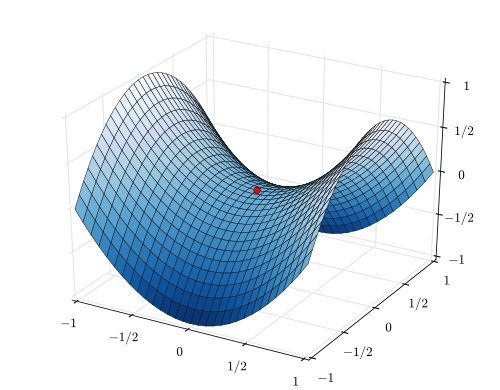
类比地理中的鞍部,这个点被称作鞍点。
那么,该怎么做呢,数学家想到了一种方法——二阶偏导法。
令
[A=f_{xx}(x_0,y_0),B=f_{xy}(x_0,y_0),C=f_{yy}(x_0,y_0)
]
则有
[A imes C-B^2>0 ext{$large 且$} A>0==> ext{$large 极小值$}
]
[A imes C-B^2>0 ext{$large 且$} A<0==> ext{$large 极大值$}
]
[A imes C-B^2<0==> ext{$large 鞍点$}
]
[A imes C-B^2==0 ==> ext{$large 无法确定$}
]
二元函数最值
最值问题和极值问题相比,最大的区别就是最值问题可以通过比较各点的值来计算。我们可以通过求出所有极值点甚至非极值点的值来得出最终的答案。既然如此,我们可以求出所有可能的点(各偏导等于零的点)并计算得到最终答案。