【机器学习算法基础+实战系列】逻辑斯蒂回归

二项逻辑斯蒂回归模型

构建预测函数

Logistic Regression 虽然是名字带有回归，但是本质上是一种分类方法，一般情况下用于二分类的情况（也就是说输出情况一般是有两种）
我们想要的函数是能够接受所有的输入，然后预测出来类别。在这里我们引入Sigmoid函数。函数形式如下

[g(z)=frac{1}{1+e^{-z}} ]

图像如下所以:

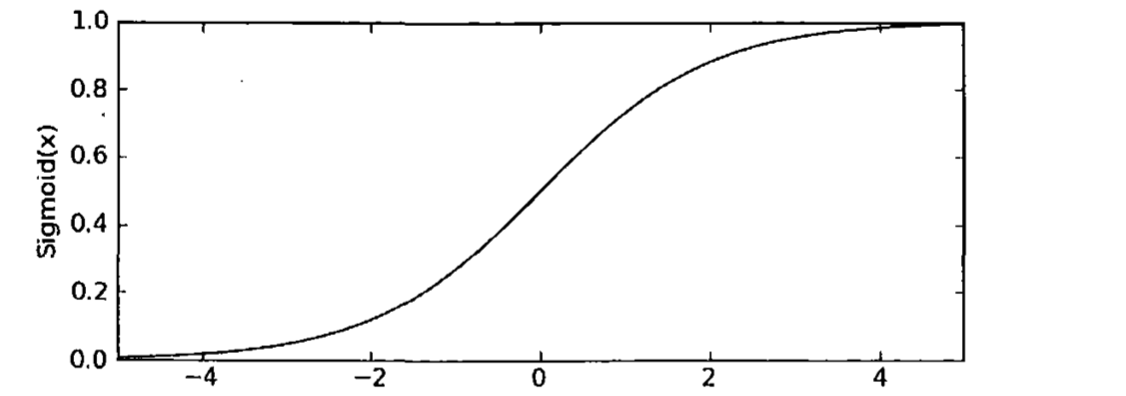
对于Sigmoid函数的输入z，有以下的公式给出:
(z=w_{0}x_{0}+w_{1}x_{1}+w_{2}x_{2}...w_{n}x_{n}=w^{T}x)
所以预测函数可以写成这个样子:$$h_{w}(x)=g(w^{{T}x)=frac{1}{1+e}{-w^{T}x}}$$
对于这个预测函数，是具有特殊含义的，它表示结果取1的概率，因此对于输入x分类结果为类别1和类别0的概率分别是：

[P(y=1|x;w)=h_{w}(x) ]

[P(y=0|x;w)=1-h_{w}(x) ]

事件结果为1和结果为0（事件发生与不发生）的概率之比为：

[frac{h_{w}(x)}{1-h_{w}(x)}=e^{w^{T}x} ]

我们将这个比值称之为事件的发生比（the odds of experiencing an event），简称为odds
对odds取对数，我们可以得到$$log(frac{p}{1-p})=w_{0}x_{0}+w_{1}x_{1}+w_{2}x_{2}...w_{n}x_{n}$$

构造损失函数(Cost function):

常见的损失函数：

0-1损失函数

[egin{eqnarray}L(Y,f(X))== egin{cases} 1, &Y e f(X)cr 0, &Y=f(X)cr end{cases} end{eqnarray}]

平方损失函数

[L(Y,f(X)) = (Y-f(x))^{2} ]

绝对值损失函数

[L(Y,f(X))=|Y-f(X)| ]

对数损失函数

[L(Y,P(Y|X))=-logP(Y|X) ]

逻辑回归之中我们采取的就是对数损失函数，如果损失函数值越小，表示模型越好。
根据上面的内容我们可以得到我们的对数损失函数公式：

[egin{eqnarray}cost(h_{w}(x),y)== egin{cases} -log(h_{w}(x)), &y= 1cr -log(1-h_{w}(x))&y=0cr end{cases} end{eqnarray}]

这个损失函数其实是通过对数最大似然估计得到的。我们将上面的两个式子合二为一，就可以单个样本的损失函数得到：

[cost(h_{w}(x),y)=-y_{i}log(h_{w}(x))-(1-y_{i})log(1-h_{w}(x)) ]

全体样本的损失函数就可以表示为:

[cost(h_{w}(x),y)=sum_{i=1}^{m}(-y_{i}log(h_{w}(x))-(1-y_{i})log(1-h_{w}(x))) ]

从而我们可以得到平均损失函数为

[frac{1}{m}cost(h_{w}(x),y)=frac{1}{m}sum_{i=1}^{m}(-y_{i}log(h_{w}(x))-(1-y_{i})log(1-h_{w}(x))) ]

对于这个式子我们按下不表，接下来我们使用最大似然估计的方法求得对数似然函数,推导公式如下:

[P(y|x;w)=((h_{w}(x))^{y}(1-h_{w}(x))^{1-y}) ]

取似然函数为:

[L(w)=prod_{i=1}^{m}P(y_{i}|x_{i};w) ]

[Rightarrow prod_{i=1}^{m}(h_{w}(x_{i}))^{y_{i}}(1-h_{w}(x_{i}))^{1-y_{i}} ]

对数似然函数为:

[l(w)=logL(w) ]

[Rightarrow sum_{i=1}^{m}(y_{i}logh_{w}(x_{i})+(1-y_{i})log(1-h_{w}(x_{i}))) ]

可以看到我们的损失函数和最后得到的对数似然函数形式上是一样的，所以求似然函数的最大值就是求损失函数的最小值，得到的参数应该是同样的。
然后我们对(l(w))进行化简，推导公式如下:

[l(w)=sum_{i=1}^{m}y_{i}frac{logh_{w}(x_{i})}{log(1-h_{w}(x_{i}))}+sum_{i=1}^{m}log(1-h_{w}(x_{i})) ]

[Rightarrow sum_{i=1}^{m}y_{i}w^{T}x-sum_{i=1}^{m}(1+e^{w^{T}x}) ]

对(l(w))求导:

[frac{partial l(w)}{partial w}=sum_{i=1}^{m}y_{i}x_{i}-sum_{i=1}^{m}frac{1}{1+e^{-w^{T}x_{i}}}x_{i} ]

[Rightarrow sum_{i=1}^{m}(y_{i}-h_{w}(x_{i}))x_{i} ]

优化求解

1.梯度下降算法：
接下来我们使用梯度上升算法针对似然函数进行参数的迭代（或者使用梯度下降算法针对损失函数进行参数的迭代）:

[w_{t+1}=w_{t}+alpha frac{partial l(w)}{partial w} ]

[Rightarrow w_{t}+alpha sum_{i=1}^{m}(y_{i}-h_{w}(x_{i}))x_{i} ]

梯度下降算法的伪代码为：
每个回归系数初始1
重复R次:
计算整个数据集的梯度
使用alphax gradient更新回归系数的向量
返回回归系数

《机器实战》中这一章节例子代码如下（与原书代码相比，导入文件函数以及对数据的操作代码有改动，梯度下降代码没有改动）

import numpy as np
import pandas as pd
def sigmoid(inX):# You should note that the input of the function(like inX) should be matrix or just one number(not the numpy.array). 
    # so if the inX is list, you can just use mat function(mat.(inX)).
    #if you get the inX like the np.array,you should use np.mat
    return 1.0/(1+exp(-inX))# To get the result of the sigmoid
def train(DF):
    DF=DF.as_matrix()#Transform the datafram into matrix
    samplenumber,featurenum=np.shape(DF)
    
    # in this module, we want to make the features' matrix
    a=DF[:,0]
    a = a[:,np.newaxis]# use tihs funciton to transform the one denmension into two denmensino which is very useful to for the np.concatenate 
    b=DF[:,1]
    b = b[:,np.newaxis]
    c=np.ones((samplenumber,1))
    dataMatrix= np.mat(np.concatenate((a,b,c),axis=1))#you can get the detail about combinning  the array in the link(http://blog.csdn.net/selous/article/details/72650426)
    labelMat = np.mat(DF[:,2]).transpose()
    #梯度下降算法
    weights = ones((featurenum,1))
    maxCycles = 500
    alpha=0.0001
    for k in range(maxCycles):
        h=sigmoid(dataMatrix*weights)
        error = (labelMat - h)
        weights = weights + alpha * dataMatrix.transpose()* error
    return weights

DF=pd.read_csv('testSet.csv')
train(DF)

2.随机梯度下降算法
我们需要注意的是，对于梯度下降（上升）算法来说，在每次更新回归系数的时候需要遍历整个数据集，所以如果数据量很大的话，时间消耗成本是很大的，我们这个时候可以采取随机梯度下降算法。
随机梯度下降算法一个最根本的就是一次可以用一个样本来更新回归系数。
伪代码如下:
所有回归系数初始化为1
对数据集中的每个样本
计算该样本的的梯度
使用alpha X gradient 更细回归系数值
返回回归系数值
代码实现如下:

def stocGradAscent1(dataMatrix, classLabels, numIter=150):
    m,n = shape(dataMatrix)
    weights = ones(n)   #initialize to all ones
    for j in range(numIter):
        dataIndex = range(m)
        for i in range(m):
            alpha = 4/(1.0+j+i)+0.0001    #apha decreases with iteration, does not 
            randIndex = int(random.uniform(0,len(dataIndex)))#go to 0 because of the constant
            h = sigmoid(sum(dataMatrix[randIndex]*weights))
            error = classLabels[randIndex] - h
            weights = weights + alpha * error * dataMatrix[randIndex]
            del(dataIndex[randIndex])
    return weights

多项逻辑斯蒂回归模型

多项逻辑斯蒂回归模型一般用于多类别分类，对其公式进行推导:
首先我们有({x_{i},y_{i}}_{i=1}^{N}, space y_{i} in {1,2,...,J}),
对上这个公式的理解就是我们有N个点的数据集，然后具有J个类别。所有我们很容易就可以知道$$P_{i,j}=P{y_{i}=j|x_{i}}$$.其中(P_{i,j})表示点i个点的类别属于第j类的概率。
并且我们可以知道$$sum_{j=1}^{J}P_{i,j}=1$$
在逻辑斯蒂二项回归模型中，我们知道这样事件发生的odds是(w^{T}x+b)(在这里为了推导公式明了，我们不需要把b带入w中去，不过本质上是一样的)
所以我们可以进而联想到这样一个公式

[logfrac{P_{i,j}}{P_{i,J}}=alpha_{j}+x_{i}eta_{j} ]

[Rightarrow P_{i,j}=P_{i,J}exp(alpha_{j}+x_{i}eta_{j}) space * ]

然后我们对*公式两边的所有(j)进行求和，得到公式如下:

[1=P_{i,J}sum_{j=1}^{J}(alpha_{i}+x_{i}eta_{j}) ** ]

而且我们可以从*公式得到:

[P_{i,J}=frac{P_{i,j}}{exp(alpha_{i}+x_{i}eta_{j})} space *** ]

我们将***公式带入到**中去，就可以得到多项逻辑斯蒂回归模型:

[P_{i,j}=frac{exp(alpha_{j}+x_{i}eta_{j})}{1+sum_{j=1}^{J-1}exp(alpha_{j}+x_{i}eta_{j})} ]

Softmax回归
Softmax 用于多分类（区别于逻辑回归的二分类问题).
假设我们有一个数组 (V)，其中(V_{i})表示数组中的第(i)个元素，那么这个元素的softmax的值就是:

[S_{i}=frac{e^{V_{i}}}{sum_{j}e^{V_{j}}} ]

换句话讲，该元素的指数与所有元素指数之和的比值。
用在多分类的情况中，我们就定义选到(y_{i})的概率是:

[P_{y_{i}}=frac{e^{f_{y{i}}}}{sum_{j}e^{V_{j}}} ]

参考二分类的损失函数，我们可以写出损失函数为:
(J(w)=sum_{j=1}^{m}sum_{i=1}^{k}1{y_{j}=i}log(frac{e^{w^{T}x}}{sum_{l=1}^{k}e^{w_{i}^{T}x}}))
其中m为训练集样本的个数，1{}为示性函数，当(y_{j}=i)成立的时候（其中类别值是1,2...k）函数值为1，否则为0

参考书籍：
机器学习算法与Python实践之（七）逻辑回归（Logistic Regression）
Logistic回归总结
 逻辑回归
 Logistic Regression 模型简介
 【机器学习算法系列之二】浅析Logistic Regression
机器学习实战
统计学习方法（李航）
机器学习之逻辑回归和softmax回归及代码示例
 Softmax 函数的特点和作用是什么？
详解softmax函数以及相关求导过程