引自:https://www.zhihu.com/question/58200555/answer/621174180
https://blog.csdn.net/weixin_45069761/article/details/106758895
为了从两个方面限制梯度:
- 当预测框与 ground truth 差别过大时,梯度值不至于过大;
- 当预测框与 ground truth 差别很小时,梯度值足够小。
考察如下几种损失函数,其中 为预测框与 groud truth 之间 elementwise 的差异:

观察 (4),当 x 增大时 L2 损失对 x 的导数也增大。这就导致训练初期,预测值与 groud truth 差异过于大时,损失函数对预测值的梯度十分大,训练不稳定。
根据方程 (5),L1 对 x 的导数为常数。这就导致训练后期,预测值与 ground truth 差异很小时, L1 损失对预测值的导数的绝对值仍然为 1,而 learning rate 如果不变,损失函数将在稳定值附近波动,难以继续收敛以达到更高精度。
最后观察 (6),smooth L1 在 x 较小时,对 x 的梯度也会变小,而在 x 很大时,对 x 的梯度的绝对值达到上限 1,也不会太大以至于破坏网络参数。 smooth L1 完美地避开了 L1 和 L2 损失的缺陷。其函数图像如下:
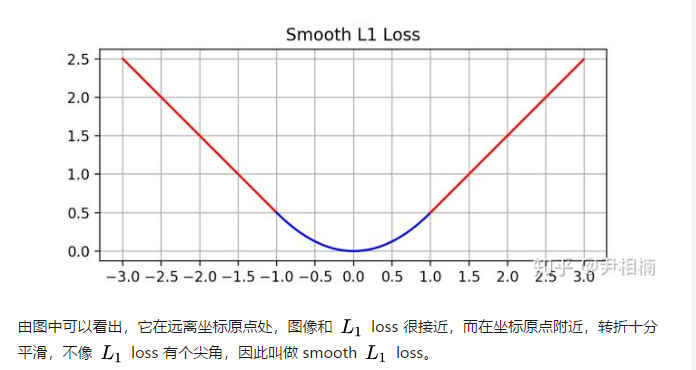
综上所述smootn l1 loss 综合了l1 loss 和l2 loss的优点。
L1正则化和L2正则化面试常考题
正则化
L1、L2都是对损失函数的优化,L范式都是为了防止模型过拟合,所谓范式就是加入参数的约束。
L1的作用是为了矩阵稀疏化。假设的是模型的参数取值满足拉普拉斯分布。
L2的作用是为了使模型更平滑,得到更好的泛化能力。假设的是参数是满足高斯分布
L1正则化和L2正则化可以看做是损失函数的惩罚项。所谓“惩罚”是指对损失函数中的某些参数做一些限制
L1正则化是指权值向量w中各个元素的绝对值之和
L2正则化是指权值向量w中各个元素的平方和然后求平方根
L1正则化和L2正则化区别
L1正则化可以产生稀疏权值矩阵,即产生一个稀疏模型,可以用于特征选择
L2正则化可以防止模型过拟合;一定程度上,L1也可以防止过拟合
正则化为什么能降低过拟合程度?并且说明下下L1正则化和L2正则化。
降低过拟合程度:正则化之所以能够降低过拟合的原因在于,正则化是结构风险最小化的一种策略实现。给loss function加上正则化项,能使得新得到的优化目标函数h = f+normal,需要在f和normal中做一个权衡(trade-off),如果还像原来只优化f的情况下,那可能得到一组解比较复杂,使得正则项normal比较大,那么h就不是最优的,因此可以看出加正则项能让解更加简单,通过降低模型复杂度,得到更小的泛化误差,降低过拟合程度。
L1正则化和L2正则化:L1正则化就是在loss function后加正则项为L1范数,加上L1范数容易得到稀疏解(0比较多)。L2正则化就是loss function后加正则项为L2范数的平方,加上L2正则相比于L1正则来说,得到的解比较平滑(不时稀疏)。但是同样能够保证解中接近于0(但不是等于0,所以相对平滑)的维度比较多,降低模型的复杂度。
为什么 L1 正则容易产生稀疏解(很多参数=0)
(1) 从解空间形状方面考虑
把W的解限制在黑色区域内,同时使得经验风险尽可能小,因此取交点就是最优解,从图中可以看出,L2正则化相当于为参数定义了一个圆形的解空间,而L1正则化相当于为参数定义了一个菱形的解空间。L1“棱角分明”的解空间显然更容易与目标函数等高线在脚点碰撞。更容易在棱角取得交点,从而导致出现参数为0的情况,从而产生稀疏解
(2) 从函数叠加方面考虑
可以看到,在加入L1正则项后,最小值在红点处,对应的w是0。而加入L2正则项后,最小值在黄点处,对应的w并不为0。
为什么呢?加入L1正则项后,目标函数变为L(w)+C|w|,单就正则项部分求导,原点左边的值为-C,原点右边的值为C,因此,只要原目标函数的导数绝对值|L’(w)|<C,那么带L1正则项的目标函数在原点左边部分始终递减,在原点右边部分始终递增,最小值点自然会出现在原点处。
加入L2正则项后,目标函数变为L(w)+Cw2,只要原目标函数在原点处的导数不为0,那么带L2正则项的目标函数在原点处的导数就不为0,那么最小值就不会在原点。因此L2正则只有见效w绝对值的作用,但并不能产生稀疏解
(3)从贝叶斯先验角度考虑
从贝叶斯角度来看,L1正则化相当于对模型参数w引入了拉普拉斯先验,L2正则化相当于引入了高斯先验
可以看到,当均值为0时,高斯分布在极值点处是平滑的,也就是高斯先验分布认为w在极值点附近取不同值的可能性是接近的。但对拉普拉斯分布来说,其极值点处是一个尖峰,所以拉普拉斯先验分布中参数w取值为0的可能性要更高
写的很详细1
写的很详细2
L2为什么能降低过拟合
在不使用L2正则化时,求导结果中w前系数为1,现在w前面系数为 1−ηλ/n ,因为η、λ、n都是正的,所以 1−ηλ/n小于1,它的效果是减小w,这也就是权重衰减(weight decay)的由来,更小的权值w,从某种意义上说,表示网络的复杂度更低,对数据的拟合刚刚好(这个法则也叫做奥卡姆剃刀)
参考文章1
参考文章2
L1和L2比较分析
(1) 鲁棒性
L1鲁棒性比L2更好
L1对异常点不太敏感,而L2则会对异常点存在放大效果
L1-norm(最小绝对值偏差)相比于L2-norm(最小均方),它的鲁棒性更好,对数据中的异常点有很好的抗干扰能力,异常点可以安全的和高效的忽略,如果异常值对研究很重要,最小均方误差则是更好的选择。
对于L2-norm,由于是均方误差,如果误差>1的话,那么平方后,相比L1-norm而言,误差就会被放大很多,因此模型会对样例更敏感
(2) 稳定性
L2比L1更稳定
对于新数据的调整,L1的变动很大,而L2的则整体变动不大
假设我们把绿色的点向右移动一点,L2维持了和原回归线一样的形状,可是在L1样例中,回归线的斜率更陡了,并且影响到了其它点的预测值,假设我们把绿色的点水平向右移动得更远,L2变化了一点,但是L1变化更大了,L1的斜率完全改变了,
只要数据点的稍稍调整,L1回归线就会变化很多,这就是L1不稳定性的表现之处








