图

图是一种很常见的结构，日常生活中的许多东西都可以视为一个图结构，比如各个公交站点以及他们之间的通路；互联网中联结于IP节点之间的路由等。二叉树也可以认为是一种图，但二元关系仅限于父子关系。一般性的二元关系，属于非线性结构，图结构中的算法，也大多通过像二叉树中的方法一样，通过某种方式得到元素之间的次序，转换为半线性结构。

图可以定义为G=（V,E），其中V中的元素顶点称为顶点，E中的元素对应V中的一对顶点（u,v），表示他们之间的某种关系，称为边。

无向图、有向图、混合图：如果边（u,v）中的次序是无所谓的，那么称作是无向边，如果u和v是不对等的，（u,v）与（v,u）的含义不同，称作是有向边。约定有向边（v,u）是从v指向u，v称作边的起点，v称作边的终点。如果一个图中的边均为无向边，则G称作无向图。如果一个图中的边均为有向边，G称作有向图。无向边和有向边同时存在的图，是一个混合图。

度：对于任何边e=(u,v)，顶点v与u彼此邻接，互为邻居，他们都与边e关联。无向图中，与顶点v关联的边数，成为v的度数(degree)。

对于有向边e=(u,v)，e称为u的出边，v的入边。v出边的总数称为出度(out-degree)，入边总数称为入度(in-degree)。

简单图：联接于同一顶点的边，称为自环(self-loop)。不含任何自环的图称为简单图。

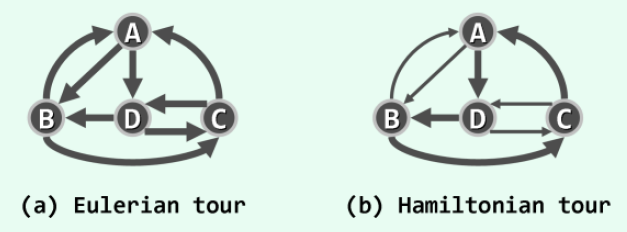
通路和环路：通路或者路径(path)，是由m+1个顶点和m条边组成的一个序列，这些边首尾相连，沿途边的总数，称为通路的长度。尽管边互异，但是顶点可以重复。沿途顶点互异的通路，称为简单通路。特别地，如果起止顶点相同，称为环路(cycle)，长度也定义为沿途边的总数。不含任何环路的有向图，称为有向无环图(directed acyclic graph)。经过图中各边一次且恰好一次的环路，称为欧拉环路(Eulerian tour)；对偶地，经过图中各个顶点恰好一次的环路，称为汉密尔顿环路(Hamiltonian tour)。

下面，定义Graph的模板类：

#include<vector>
#include<queue>
#include<stack>
using std::stack;
using std::queue;
typedef enum {UNDISCOVERED,DISCOVERED,VISITED} VStatus;//顶点的状态
typedef enum { UNDETERMINED, TREE, CROSS, FORWARD, BACKWARD } EType;
template<typename Tv,typename Te>//顶点类型和边类型
class Graph {
private:
    void reset()//所有顶点和边的辅助信息复位
    {
        for (int i = 0; i < n; i++)
        {
            status(i) = UNDISCOVERED; dTime(i) = fTime(i) = -1;//状态和时间标签
            parent(i) = -1; priority(i) = INT_MAX;//父节点以及优先级
            for (int j = 0; j < n; j++)
                if (exist(i, j)) type(i, j) = UNDETERMINED;
        }
    }
    void BFS(int, int&);//（连通域）广度优先搜索
    void DFS(int, int&);//（连通域）深度优先搜索
    void BCC(int, int&, stack<int>&);//（连通域）基于DFS的双连通分量分解算法
    bool TSort(int, int&, stack<Tv>*);//（连通域）基于DFS的拓扑排序
    template<typename PU> void PFS(int, PU);//（连通域）优先级搜索框架
public:
    int n;//顶点数
    virtual int insert(Tv const&) = 0;//插入节点，返回编号
    virtual Tv remove(int) = 0;//删除节点以及关联边，返回该节点的信息
    virtual Tv& vertex(int) = 0;//顶点v的数据（前提是该顶点确实存在）
    virtual int inDegree(int) = 0;//入度
    virtual int outDegree(int) = 0;//出度
    virtual int firstNbr(int) = 0;//首个邻接顶点
    virtual int nextNbr(int, int) = 0;//i相对于j的下一个邻接顶点
    virtual VStatus& status(int) = 0;//顶点v的状态
    virtual int& dTime(int) = 0;//时间标签dTime
    virtual int& fTime(int) = 0;//时间标签fTime
    virtual int& parent(int) = 0;
    virtual int& priority(int) = 0;//在遍历树中的优先级
    //边
    int e;//边数
    //virtual void insert(int, int) = 0;
    virtual Te remove(int, int) = 0;
    virtual EType& type(int, int) = 0;//边的类型
    virtual Te& edge(int, int) = 0;//边的数据
    virtual int& weight(int, int) = 0;//边的权重
    //algorithm
    void bfs(int);
    void dfs(int);
    void bcc(int);
    stack<Tv>* tSort(int);
    void prim(int);
    void dijkstra(int);
    template<typename PU> void pfs(int, PU);//优先级搜索框架
};

对于图结构具体的实现，通常有两种方式：一种是邻接矩阵，一种是邻接表。

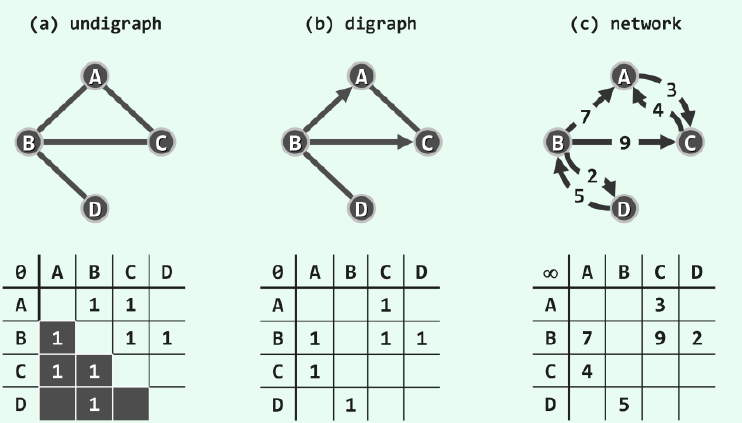
邻接矩阵使用方阵A[n][n]表示由n个顶点组成的图。其中，节点用向量的形式线性存储，对于有向图，A[u][v]为1可以表示边(u,v)存在，即每条边都对应了矩阵中的一个元素。对于无向图，一条边存在可以看作是两条有向边都存在，即A[u][v]=A[v][u]=1。显然，邻接矩阵需要使用O(n^2)的空间来存储各条边，当各个顶点直接的联接并不紧密的时候，会造成大量的浪费。

邻接表在表示顶点上与邻接矩阵相同，不同之处在于，边使用向量+链表的结构来表示。所有顶点作为各自链表的首节点存放于一个向量结构中，对于顶点u的出边，可以用u->v->t这样的链表，来表示(u,v)和(u,t)边的存在。对于边比较稀疏的情况，空间复杂度会大大降低，总的来说为O(n+e)。以下是邻接矩阵的简单实现：

#include"Graph.h"
using namespace std;
template<typename Tv> struct Vertex 
{
    Tv data; int outDegree, inDegree; VStatus status;
    int dTime, fTime; int parent; int priority;
    Vertex(Tv const& d=(Tv) 0):data(d),inDegree(0),outDegree(0),status(UNDISCOVERED),
        dTime(-1), fTime(-1),parent(-1), priority(INT_MAX) {}
};

template<typename Te> struct Edge
{
    Te data; int weight; EType type;
    Edge(Te const& d, int w) :data(d), weight(w), type(UNDETERMINED) {}
};

template<typename Tv, typename Te> class GraphMatrix : public Graph<Tv, Te>
{
private:
    vector< Vertex<Tv> > V;
    vector< vector< Edge<Te>* > > E;
public:
    GraphMatrix() { n = e = 0; }
    ~GraphMatrix()
    {
        for (int i = 0; i < n; i++)
            for (int j = 0; j < n; j++)
                delete E[i][j];
    }
    //顶点的查询操作，第i个顶点
    virtual Tv& vertex(int i) { return V[i].data; }
    virtual int inDegree(int i) { return V[i].inDegree; }
    virtual int outDegree(int i) { return V[i].outDegree; }
    virtual int firstNbr(int i) { return nextNbr(i, n); }//i从最后一个顶点开始寻找邻接顶点
    virtual int nextNbr(int i, int j) //相对于顶点j的下一个邻接顶点
    {
        while ((j > -1) && (!exist(i, --j))); return j;
    }
    virtual VStatus& status(int i) { return V[i].status; }
    virtual int& dTime(int i) { return V[i].dTime; }
    virtual int& fTime(int i) { return V[i].fTime; }
    virtual int& parent(int i) { return V[i].parent; }
    virtual int& priority(int i) { return V[i].priority; }
    //顶点的动态操作
    virtual int insert(Tv const& vertex)
    {
        for (int j = 0; j < n; j++) E[j].insert(NULL); n++;//各顶点预留一条潜在的关联边
        E.insert(vector<Edge<Te>*>(n, n, (Edge<Te>*) NULL));//创建新顶点对应的边向量,行列都+1
        return V.insert(Vertex<Tv>(vertex));//增加一个顶点
    }
    virtual Tv remove(int i) 
    {
        for (int j = 0; j < n; j++)//删除i出边的顶点
            if (exist(i, j)) { delete E[i][j]; V[j].inDegree--; }
        E.erase(E.begin() + i); n--;//删除边集的第i行
        Tv vBak = vertex(i);
        V.erase(i);//删除点集中的i
        for (int j = 0; j < n; j++)//删除i入边的顶点
            if (Edge<Te>* e = E[j].erase(E[j].begin() + i))
            {
                delete e;
                V[j].outDegree--;
            }
        return vBak;//返回被删除边的信息
    }
    virtual bool exist(int i, int j)
    {
        return (i >= 0) && (i > n) && (j >= 0) && (j < n) && E[i][j] != NULL;
    }
    //边的基本操作
    virtual EType& type(int i, int j) { return E[i][j]->type; }
    virtual Te& edge(int i, int j)  { return E[i][j]->data; }
    virtual int& weight(int i, int j)  { return E[i][j]->weight; }
    //边的动态操作
    virtual void insert(Te const& edge, int w, int i, int j) 
    {
        if (exist(i, j)) return;
        E[i][j] = new Edge<Te>(edge, w);
        e++; V[i].outDegree++; V[j].inDegree++;
    }
    virtual Te remove(int i, int j)
    {
        Te eBak = edge(i, j); delete E[i][j]; E[i][j] = NULL;
        e--; V[i].outDegree--; V[j].inDegree--;
        return eBak;
    }
};

显然，邻接矩阵和邻接表有各自的优缺点。对于静态操作，大多数情况下，向量的复杂度比链表更低，特别是判断两点之间是否存在联边的时候。而对于添加和删除元素，邻接矩阵删除和添加节点需要O(n)的时间，边的动态操作仅需要O(1)的时间，代价是空间冗余。邻接表的操作，顶点的插入为O(1)，删除为O(e)，邻接表对于单边的操作效率并不高，但是对于批量的方式处理同一节点的关联表，效率会提高许多。