1 一阶线性近似
函数 f(x) 的一阶导数为 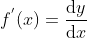 ,使用较小变化量代替微分量得
,使用较小变化量代替微分量得  ,令
,令 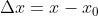 ,
,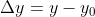 ,
,
进一步整理得 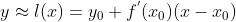 ,当已知
,当已知 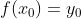 ,则可以求解
,则可以求解 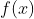 的一阶近似解为 y。
的一阶近似解为 y。
2 求解近似解
1)函数 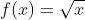 ,求解 f(11) ?
,求解 f(11) ?
已知 f(9) = 3,使用线性近似得  。
。
2)函数  ,求解 f(.99) ?
,求解 f(.99) ?
已知 f(1) = 0,使用线性近似得  。
。
3 常用函数的一阶近似(x 在 0 附近)
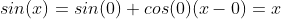


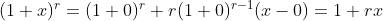
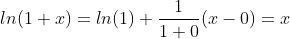
4 一阶线性近似误差
原函数使用泰勒级数展开为  ,
,
误差函数可表示为  ,
,
由于  远大于
远大于  ,误差函数可近似表达为
,误差函数可近似表达为 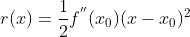 ,
,
当  时,线性近似值低于真实值;当
时,线性近似值低于真实值;当 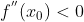 时,线性近似值高于真实值。
时,线性近似值高于真实值。
5 雅可比矩阵
当函数输入输出变量均为向量时,已知  ,求解
,求解  附近
附近  的线性近似值?
的线性近似值?
类似的,有 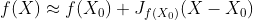 ,其中
,其中  表示函数
表示函数  在
在 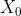 处的一阶偏导构成的矩阵,即为雅可比矩阵。
处的一阶偏导构成的矩阵,即为雅可比矩阵。
令  ,
,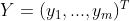 ,函数
,函数 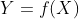 可改写方程组
可改写方程组  ,
,
分别求解方程组中每一个函数的一阶近似为 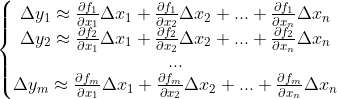 ,
,
整理成矩阵形式为  ,
, ,
,
 附近
附近  的线性近似值可表示为
的线性近似值可表示为  。
。
6 牛顿法求解方程
给定方程 f(x) = 0,由于并不是每一个方程都可以轻松求解准确解,可以使用牛顿法求解近似解。方法如下:
1)找到一个猜测解,记录为 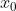 ,给出该点处线性方程为
,给出该点处线性方程为 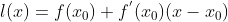 ;
;
2)寻找线性方程在 X 轴上交点位置 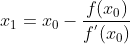 ,一般情况下,该交点位置是方程 f(x) = 0 的一个更好的近似解;
,一般情况下,该交点位置是方程 f(x) = 0 的一个更好的近似解;
3)重复 2)直到  足够接近 0 为止。
足够接近 0 为止。
牛顿法并不一定能够迭代出足够精确的解,当第一个猜测解位置较远时,可能无法得到一个正确的解。猜测解的主要原则是猜测解与真实解区间的一阶导数符号一致,且比较接近。
以下某些情形,可能导致牛顿法失效,主要包括:
1)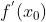 接近 0,迭代过程
接近 0,迭代过程 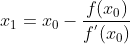 使得
使得 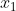 无限远离
无限远离 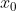 ;
;
2)f(x) = 0 存在多个解,使得收敛解与期望解不一致;
3)其他一些无限循环情况;
总之,在迭代过程中需要判断迭代解收敛情况,根据收敛情况判断是否可以通过牛顿法寻找近似解。
7 高阶近似
使用一阶线性近似时,其误差值为 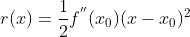 ,为了得到一个更加精确的近似值,可以使用二阶近似,公式如下:
,为了得到一个更加精确的近似值,可以使用二阶近似,公式如下:
 ,其近似误差为
,其近似误差为 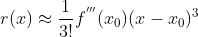 。
。
令 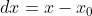 ,
, 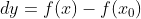 ,
,
一阶近似可表示为  , 对函数求导数得
, 对函数求导数得 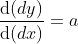 ,由于
,由于  ,得
,得  ;
;
二阶近似可表示为  ,对函数求二阶导数得
,对函数求二阶导数得 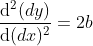 ,由于
,由于 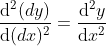 ,得
,得 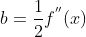 ;
;
同理,可以求得N阶近似各项系数为 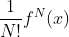 。
。
参考资料 The Calculus Lifesaver Adrian Banner