对于正定矩阵 A 可被分解为 
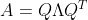
 ,其中,Q 为正交矩阵,
,其中,Q 为正交矩阵, 在对角线上元素均为正值;
在对角线上元素均为正值;
对于任意矩阵 A(方阵或长方形矩阵),可以分解为  ,其中,U,V 为两个不相同的正交矩阵,
,其中,U,V 为两个不相同的正交矩阵, 在对角线上元素均为正值;
在对角线上元素均为正值;
在矩阵 A 的行空间与零空间上任意选择正交单位向量  ,对每一个向量做线性变换
,对每一个向量做线性变换 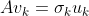 ,使得
,使得 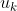 位于矩阵 A 的列空间或者左零空间的单位向量;
位于矩阵 A 的列空间或者左零空间的单位向量;
使用矩阵形式表示为  ,
,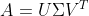 ;
;
由于  为任意选择正交单位向量,无法确保 U 也为正交向量,所以需要重新选择
为任意选择正交单位向量,无法确保 U 也为正交向量,所以需要重新选择  ;
;
令  为
为  的特征向量,由于
的特征向量,由于  为正定矩阵,所以
为正定矩阵,所以  相互正交,通过如下变换可选择另一组正交向量 U:
相互正交,通过如下变换可选择另一组正交向量 U:
 ,
, ,则
,则  为
为 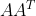 的一组特征向量,
的一组特征向量,
由于 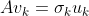 ,所以
,所以 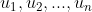 也为一组正交向量;
也为一组正交向量;
到此,可以将矩阵 A 分解为  ,U,V 均为正交矩阵,利用
,U,V 均为正交矩阵,利用 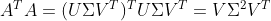 可求解
可求解  ;
;
综上所述,SVD 分解可按如下步骤进行:
1)求矩阵  的一组归一化特征向量
的一组归一化特征向量  ,该组特征向量构成矩阵 V;
,该组特征向量构成矩阵 V;
2)求矩阵  的特征值矩阵,将对角线上元素开平方即为
的特征值矩阵,将对角线上元素开平方即为  矩阵;
矩阵;
3)使用 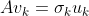 得到一组归一化特征向量
得到一组归一化特征向量 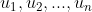 ,该组特征向量构成矩阵 U,完成 SVD 分解;
,该组特征向量构成矩阵 U,完成 SVD 分解;
以上给出了 SVD 分解方法,下面使用 SVD 求解不可解方程:
1)对于对角矩阵构成的方程组  ,该方程组没有解,但方程组
,该方程组没有解,但方程组 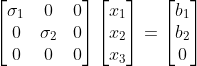 的解可为其最优解;
的解可为其最优解;
因此,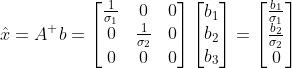 ,其中,
,其中, 为矩阵 A 的伪逆;
为矩阵 A 的伪逆;
2)对矩阵 A 进行 SVD 分解为 ![]() ,而
,而 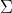 的伪逆就是对对角线上非零元素求倒数,且U,V均为正交矩阵,故
的伪逆就是对对角线上非零元素求倒数,且U,V均为正交矩阵,故 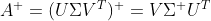 ;
;
3)求解 Ax=b 等价于  ,带入
,带入 ![]() 得
得  ,
,
由于 U 为正交矩阵,满足 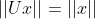 ,可继续改写为
,可继续改写为 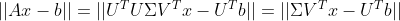 ,
,
令 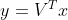 ,上式变换为
,上式变换为  ,
,
而 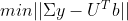 等价于
等价于 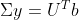 ,已知如何求解
,已知如何求解 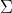 的伪逆,故
的伪逆,故 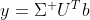 ,
,
带入 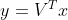 得
得  ,
,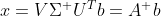 ;
;
参考资料 Linear Algebra And Its Applications Gilbert Strang