序列型动态规划
- 给定一个序列
- 动态规划方程f[i]中的下标i表示前i个元素a[0],a[1],...,a[i-1]的某种性质
-坐标型的f[i]表示以ai为结尾IDE某种性质
- 初始化中,f[0]表示空序列的性质
-坐标型动态规划的初始条件f[0]就是指以a0为结尾的子序列的性质
例题
Paint House II
题目分析
- 这题和Paint House非常类似,只是颜色种类变成K种
- 动态规划思路和Paint House一样,需要记录尤其前i栋房子并且房子i-1是颜色1,颜色2,...,颜色k的最小花费:
f[i][1], f[i][2], ... , f[i][K]
动态规划组成部分二:转移方程
- 设油漆前i栋房子并且房子i-1是颜色1,颜色2,... ,颜色K的最小花费分别为法f[i][1], f[i][2], .... ,f[i][K]
f[i][1] = min{f[i - 1][2] + cost[i - 1][1], f[i - 1][3] + cost[i - 1][1], ... ,f[i - 1][K] + cost[i - 1][1]}
f[i][2] = min{f[i - 1][1] + cost[i - 1][2], f[i - 1][3] + cost[i - 1][2], ... ,f[i - 1][K] + cost[i - 1][2]}
...
f[i][K] = min{f[i - 1][1] + cost[i - 1][K], f[i - 1][2] + cost[i - 1][K], ... ,f[i - 1][K-1] + cost[i-1][K]}
- 设油漆前i栋房子并且房子i - 1是颜色1,颜色2,.... ,颜色K的最小花费分别为f[i][1], f[i][2], ... , f[i][K]
- 直接计算的时间复杂度(计算步数):
-i从0到N
-j从1到K
-k从1到K
-O(NK2)
动态规划常见优化
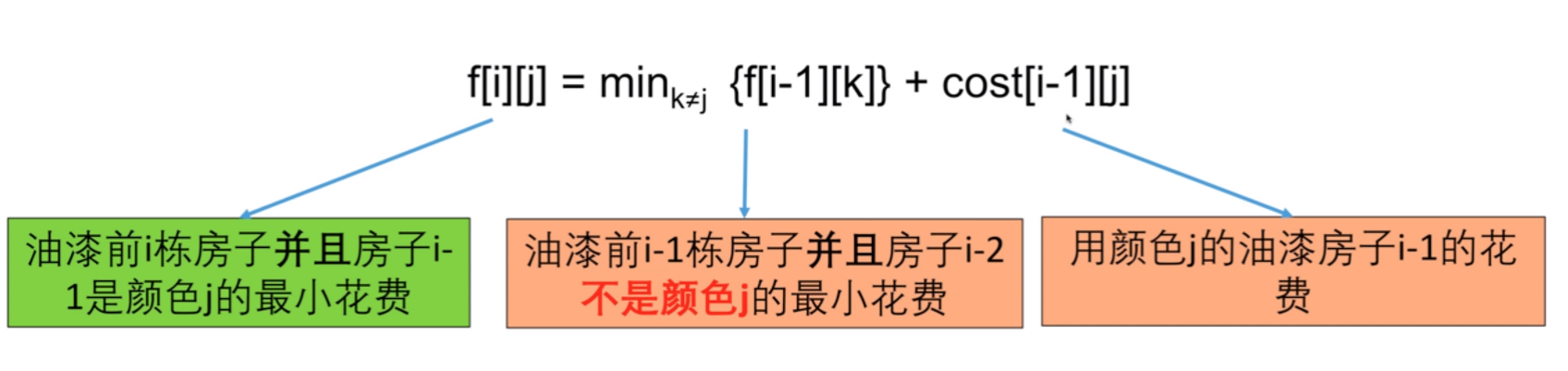
- f[i][j] =mink≠j{f[i - 1][k]} + cost[i - 1][j]
- 每次需要求f[i - 1][1],...,f[i - 1][K]中除了一个元素之外其他元素的最小值

- 记录下f[i - 1][1], ... ,f[i - 1][K]中的最小值和次小值分别是哪个
- 假如最小值是f[i - 1][a],次小值是f[i - 1][b]
- 则对于j = 1,2,3,... ,a - 1, a + 1, .... , K, f[i][j] = f[i - 1][a] + cost[i - 1][j]
- f[i][a] = f[i - 1][b] + cost[i - 1][a]
- 时间复杂度降为O(NK)
House Robber
动态规划组成部分一:确定状态
- 最后一步:窃贼的最优策略中,有可能偷或者不偷最后一栋房子N-1
- 情况1:不偷房子N-1
-简单,最优策略就是前N-1栋房子的最优策略
- 情况2:偷N-1
-仍然需要知道在前N-1栋房子中最多能偷多少金币,但是,需要保证不偷第N-2栋房子
- 如何知道在不偷房子N-2的前提下,在前N-1栋房子中最多能偷多少金币呢?
-用f[i][0]表示不偷房子i-1的前提下,前i栋房子中最多能偷多少金币
-用f[i][1]表示偷房子i-1的前提下,前i栋房子中最多能偷多少金币
动态规划组成部分二:转移方程
- 设f[i][0]为不偷房子i-1的前提下,前i栋房子中最多能偷多少金币
- 设f[i][1]为偷房子i-1的前提下,前i栋房子中最多能偷多少金币


简化
- 在不偷房子i-1的前提下,前i栋房子中最多能偷多少金币
-其实这就是前i-1栋房子最多能偷多少金币
- 所以我们可以简化前面的表示
动态规划组成部分三:初始条件和边界情况
- 设f[i]为窃贼在前i栋房子最多偷多少金币
- f[i] = max{f[i-1], f[i-2] + A[i - 1]}
- 初始条件:
-f[0] = 0(没有房子,偷0枚金币)
-f[1] = A[0]
-f[2] = max{A[0], A[1]}
动态规划组成部分四:计算顺序
- 初始化f[0]
- 计算f[1], f[2], .... , f[n]
- 答案是f[n]
- 时间复杂度O(N),空间复杂度O(1)
House Robber II
题意分析
- 这题和House Robber非常类似,只是房子现在排成一个圈
- 于是房子0和房子N-1成了邻居,不能同时偷盗
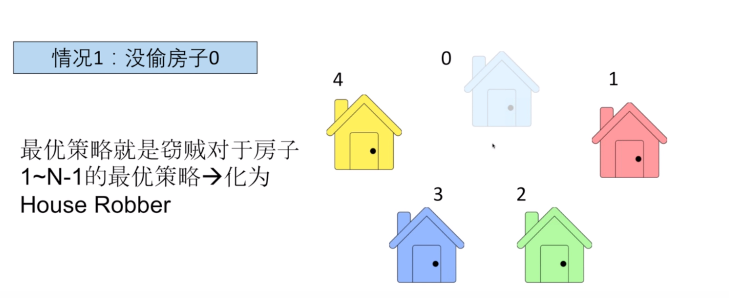
- 要么没偷房子0
- 要么没偷房子N-1
- 我们可以枚举窃贼是没有偷房子0还是没有偷房子N-1

小结
- 圈的情况比序列复杂
- 但是,通过对于房子0和房子N-1不能同时偷的原理,进行分情况处理
- 经过处理,变成序列情况
- 问题迎刃而解
Best Time To Buy And Sell Stock
题意分析
- 保底策略:什么都不做,利润0
- 低卖高卖,先买后买
- 如果买卖一股,一定是第i天买,第j天卖(j > i),获利是Pj - Pi
- 枚举j,即第几天卖
- 显然,希望找到最小的买入价格Pi(i < j)
动态规划解法
- 从0到N-1枚举j,即第几天卖
- 时刻保存当前为止(即0 ~ j-1天)的最低价格Pi
- 最大的Pj - Pi即为答案
Best Time To Buy And Sell Stock II
题意分析
- 买卖任意多次
- 正确性证明可以从这里下手:
-如果最优策略第10天买,第15天卖,我们可以把它分解成5天,结果不会变差
Best Time To Buy And Sell Stock III
题意分析
- 题目大意和I,II基本类似
- 只能最多两次买卖
- 所以需要记录已经买卖了多少次
动态规划组成部分一:确定状态
- 最后一步:最优策略中,最后一次卖发生在第j天
- 枚举最后一次买发生在第几天
- 但是不知道之前有没有买卖过
记录阶段
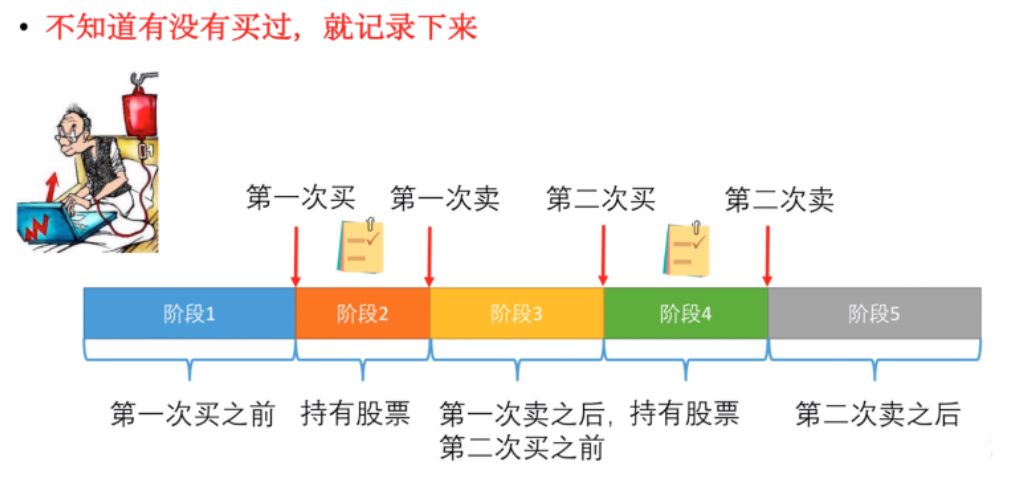
- 阶段可以保持:即不进行买卖操作
- 阶段可以变化:买或卖
-在阶段2,卖了一股后,进入阶段3
-在阶段2,卖了一股后当天买一股,进入阶段4
- 例如,如果要求前N天(第N - 1 天)结束后,在阶段5的最大获利,设为f[N][5]
-情况1:第N - 2天就在阶段5 --- f[N - 1][5]
-情况2:第N - 2天还在阶段4(第二次持有股票),第N - 1天卖掉,f[N - 1][4] + (PN-1 - PN-2)
- 例如,如果要求前N天(第N - 1 天)结束后,在阶段4的最大获利,设为f[N][4]
-情况1:第N - 2天就在阶段4 --- f[N - 1][4] + (PN-1 - PN-2)
-情况2:第N - 2天就在阶段3 --- f[N - 1][3]
-情况3:第N - 2天就在阶段2,第N - 1天卖完了立即买 --- f[N - 1][2] + (PN-1 - PN-2)
子问题
- 要求f[N][1],... ,f[N][5]
- 需要知道f[N - 1][1],.... ,f[N - 1][5]
- 子问题
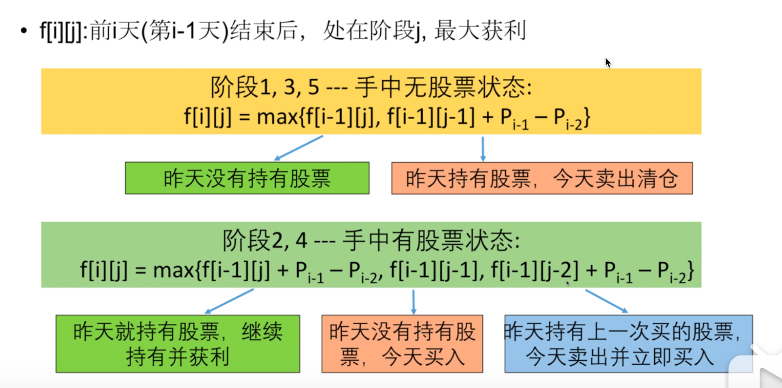
- 状态:f[i][j]表示前i天(第i - 1天)结束后,在阶段j的最大获利
动态规划组成部分二:转移方程
动态规划组成部分三:初始条件和边界情况
- 刚开始(前0天)处于阶段1
-f[0][1] = 0
-f[0][2] = f[0][3] = f[0][4] = f[0][5] = -∞
- 阶段1,3,5:f[i][j] = max{f[i - 1][j], f[i - 1][j - 1] + Pi-1 - Pi-2}
- 阶段2,4:f[i][j] = max{f[i - 1][j] + Pi-1 - Pi-2, f[i - 1][j - 1],f[i - 1][j - 2] + Pi-1 - Pi-2}
- 如果j - 1 < 1 或 j - 2 < 1 或 i - 2 < 0, 对应项不计入max
- 因为最多买卖两次,所以答案是max{f[N][1], f[N][3], f[N][5]},即清仓状态下最后一天最大获利
动态规划组成部分四:计算顺序
- 初始化f[0][1],....,f[0][5]
- f[1][1],....,f[1][5]
- ...
- f[1N[1],....,f[N][5]
- 时间复杂度:O(N),空间复杂度:O(N),优化后可以O(1),因为f[i][1...5]只依赖于f[i - 1][1...5]