Numpy的强大之处,在于它多样的模块,不同的模块自然对应着不同的解决问题的方式。Numpy中的模块有很多,这一次,主要涉及的是linalg模块(线性代数)、fft模块(快速傅里叶变换)、随机数、连续分布和离散分布(概率论)。
Example1
计算逆矩阵
# -*-coding:utf-8-*- import numpy as np import matplotlib.pyplot as plt
# 计算逆矩阵 A = np.mat("0 1 2; 1 0 3; 4 -3 8") print "A", A inverse = np.linalg.inv(A) print "Inverse of A", inverse print "Check", A * inverse |
结果如下:

注意:如果输入矩阵是奇异的或非方阵,将会抛出LinAlgError错误
Example2
求解线性方程组
# 求解线性方程组(Bx=b) B = np.mat("1 -2 1; 0 2 -8; -4 5 9") print "B", B b = np.array([0, 8, 9]) print "b", b x = np.linalg.solve(B, b) print "Solution", x print "Check", np.dot(B, x) |
结果如下:

Example3
特征值和特征向量
# 特征值和特征向量(Ax=bx) C = np.mat('3 -2; 1 0') print "C", C # eigvals()求解特征值 print "Eigenvalues", np.linalg.eigvals(C) # eig()求解特征值和特征向量,返回元祖 eigenvalues, eigenvectors = np.linalg.eig(C) print "Eigenvalues", eigenvalues print "Eigenvectors", eigenvectors for i in range(len(eigenvalues)): print "Left", np.dot(C, eigenvectors[:,i]) print "Right", eigenvalues[i] * eigenvectors |
结果如下:
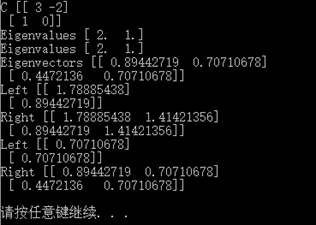
注意:eigvenvectors返回的数组要竖着看
Example4
奇异值分解SVD(将一个矩阵分解为三个矩阵的乘积)
M=U∑V*(U和V是正交矩阵,Sigma包含输入矩阵的奇异值)
# 奇异值分解 D = np.mat('4 11 14; 8 7 -2') print "D", D U, Sigma, V = np.linalg.svd(D, full_matrices=False) print "U", U print "Sihma", Sigma # 得到的Sigma只是奇异矩阵的对角值 print "V", V # 通过diag生成真正的SVD true_svd = np.diag(Sigma) print "SVD", true_svd print "Check", U * true_svd * V |
结果如下:

注意:


Example5
广义逆矩阵

# 广义逆矩阵 E = np.mat('4 11 14; 8 7 -2') print "E", E # 计算广义逆矩阵使用pinv() pseudoinv = np.linalg.pinv(E) print "Pseudo inverse", pseudoinv print "Check", E * pseudoinv |
结果如下:

Example6
行列式
# 行列式 F = np.mat('3 4; 5 6') print "F", F print "Determinant", np.linalg.det(F) |
结果如下:

Example7
快速傅里叶变换(正变换用fft,逆变换用ifft)
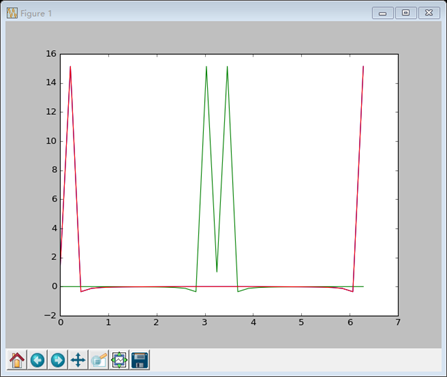
# 快速傅里叶变换 x = np.linspace(0, 2 * np.pi, 30) wave = np.cos(x) transformed = np.fft.fft(wave) i_transformed = np.fft.ifft(transformed) plt.plot(x, wave) plt.plot(x, transformed) plt.plot(x, i_transformed) plt.show() |
结果如下:

Example8
移频(将FFT输出中的直流分量移动到频谱的中央)
# 移频 x = np.linspace(0, 2 * np.pi, 30) wave = np.cos(x) transformed = np.fft.fft(wave) shifted = np.fft.fftshift(transformed) i_shifted = np.fft.ifftshift(shifted) plt.plot(x, transformed) plt.plot(x, shifted) plt.plot(x, i_shifted) plt.show() |
结果如下:
Example9
二项分布
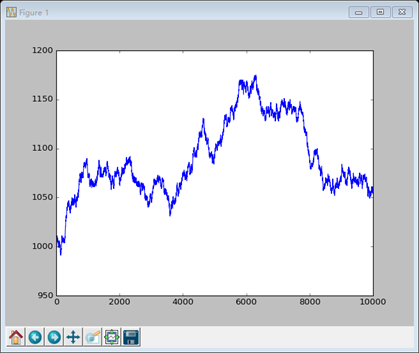
模拟赌注胡:初始资本1000,每一轮抛9枚硬币,少于5枚硬币朝上,将损失一份,否则赢得一份
# 二项分布 cash = np.zeros(10000) cash[0] = 1000 # binomial()函数 outcome = np.random.binomial(9, 0.5, size=len(cash)) for i in range(1, len(cash)): if 0 <= outcome[i] < 5: cash[i] = cash[i-1] - 1 elif outcome[i] < 10: cash[i] = cash[i-1] + 1 else: raise AssertionError("Unexpected outcome " + outcome) print outcome.min(), outcome.max() plt.plot(np.arange(len(cash)), cash) plt.show() |
结果如下:

结果很正常
Example10
超几何分布
模拟游戏秀节目:每当参赛者回答对一个问题,可以从罐子里摸出三个球并放回,罐子里有一个倒霉球,一旦被摸出,参赛者扣6分,如果摸出的三个球全部来自其余25个普通球,将加1分,如果有一百道题回答正确,得分情况怎样?
# 超几何分布 points = np.zeros(100) outcome = np.random.hypergeometric(25, 1, 3, size=len(points)) for i in np.arange(1, len(points)): if outcome[i] == 3: points[i] = points[i-1] + 1 elif outcome[i] == 2: points[i] = points[i-1] - 6 print outcome.min(), outcome.max() plt.plot(np.arange(len(points)), points) plt.show() |
结果如下:
 很合理!
很合理!

Example11
绘制正态分布

# 正态分布 # 首先产生一定数量的随机数 N = 10000 normal_values = np.random.normal(size=N) # 第二个参数bins默认为10,即柱子的数量,normed=True计算密度,而非次数 dummy, bins, dummy = plt.hist(normal_values, np.sqrt(N), normed=True, lw=1.0) sigma = 1 mu = 0 plt.plot(bins, 1/(sigma * np.sqrt(2 * np.pi)) * np.exp(-(bins-mu)**2/(2 * sigma ** 2)), lw=2.0) plt.show() |
结果如下:

总结:这次的练习,涉及到很多东西,有线性代数、快速傅里叶变换,而概率论的计算变得如此简洁明了,加上Matplotlib的应用,数形结合,效果相当好。只不过,很多函数里的参数都先当复杂,不过常规的使用中,也就那两三个参数而已。
源代码:https://github.com/Lucifer25/Learn-Python/blob/master/Numpy/exercise5.py