郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布!

arXiv:1710.10044v1 [cs.AI] 27 Oct 2017
In AAAI Conference on Artificial Intelligence (2018).
Abstract
在强化学习中,智能体通过采取动作并观察下一个状态和奖励来与环境交互。当概率采样时,这些状态转换,奖励和动作都会在观察到的长期回报中引起随机性。传统强化学习算法会对此随机性求均值以估计价值函数。在本文中,我们以最近的工作为基础,该工作提出一种采用分布方法进行强化学习的方法,在该方法中,对回报的分布进行了建模,而不是仅仅估计均值。也就是说,我们研究了学习价值分布而不是价值函数的方法。我们给出的结果弥合了Bellemare,Dabney和Munos(2017)给出的理论和算法结果之间的许多差距。首先,我们将现有结果扩展到近似分布设置。其次,我们提出了一种与我们的理论公式相一致的新颖的分布强化学习算法。最后,我们在Atari 2600游戏上评估了该新算法,发现它大大优于DQN的许多最新改进,包括相关的分布算法C51。
Introduction
在强化学习中,状态s中的动作a的价值描述了从该状态开始,选择动作a,然后遵循规定的策略所获得的期望回报或折扣奖励总和。因为知道最优策略的价值足以执行最优动作,所以它是通过经典的基于价值的方法(例如SARSA (Rummery and Niranjan, 1994) 和Q-Learning (Watkins and Dayan, 1992) )建模的目的,它们使用了Bellman方程 (Bellman, 1957) )以有效地思考价值。
最近,Bellemare, Dabney和Munos(2017)表明,随机回报的分布(其期望构成上述价值)可以通过Bellman方程的分布类似物来描述,与风险敏感的强化学习中的先前结果相呼应(Heger, 1994;Morimura et al., 2010;Chow et al., 2015)。但是,在先前的工作中,作者主张对这种价值分布本身进行建模是有用的。他们的主张是通过展示一种分布强化学习算法C51来实现的,该算法实现了基准Atari 2600游戏套件的最新技术(Bellemare et al., 2013)。
C51工作的理论贡献之一就是证明了分布Bellman算子是概率分布之间Wasserstein度量最大形式的压缩。在这种情况下,Wasserstein度量特别有趣,因为它不会受到执行Bellman更新时出现的脱节支持问题(Arjovsky, Chintala and Bottou, 2017)的困扰。不幸的是,这个结果并不能直接导致一种实用的算法:正如作者所指出的那样,并且由Bellemare et al.(2017)进一步开发,Wasserstein度量被视为一种损失,通常无法使用随机梯度法将其最小化。
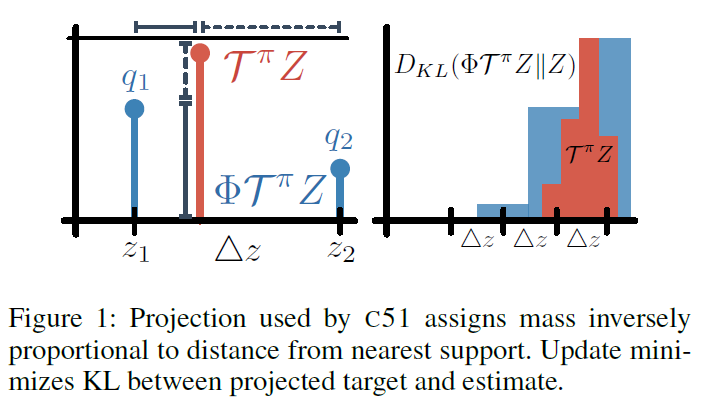
这个否定的结果使人们有疑问,是否有可能设计出一种利用压缩结果的在线分布强化学习算法。 取而代之的是,C51算法首先执行启发式投影步骤,然后最小化投影的Bellman更新和预测之间的KL差异。因此,这项工作在我们对分布强化学习的理解上留下了理论-实践上的空白,这使得难以解释C51的良好性能。因此,Wasserstein度量上端到端的分布算法的存在仍然是一个悬而未决的问题。
在本文中,我们肯定地回答了这个问题。通过诉诸分位数回归理论(Koenker, 2005),我们表明存在一种算法,该算法适用于随机近似设置,该算法可以对Wasserstein度量执行分布强化学习。
我们的方法依赖于以下技术:
- 我们从C51中“转置”参数化:前者使用N个固定位置作为其近似分布并调整其概率,我们将固定的均匀概率分配给N个可调整位置。
- 我们证明了分位数回归可以用于随机调整分布的位置,以最小化与目标分布的Wasserstein距离。
- 我们正式证明了整体算法的压缩映射结果,并使用这些结果得出结论,我们的方法可以根据需要在Wasserstein度量下端对端执行分布RL。
尽管仍然通过最大化期望来发挥作用,最初分布算法的主要兴趣在于其最先进的性能。人们自然会期望,直接将Wasserstein度量最小化而不是启发式近似会产生更好的结果。我们为我们的方法(QR-DQN)推导了Q-Learning模拟,将其应用于同一套Atari 2600游戏,并发现它可以实现更好的性能。通过使用分位数回归的平滑版本,Huber分位数回归,我们已经比最新的C51高了33%的中位数。
Distributional RL
我们通过马尔可夫决策过程(MDP) (X, A, R, P, γ) (Puterman, 1994)对智能体-环境的交互进行建模,其中X和A为状态和动作空间,R为随机变量奖励函数P(x' | x, a)在采取动作a之后从状态x转换为状态x'的概率,且折扣因子γ∈[0, 1)。策略π(· | x)将每个状态x∈X映射到A上的分布。
对于固定策略π,回报(![]() )是一个随机变量,表示沿着一个状态轨迹所观察到的折扣奖励之和。标准RL算法估算Zπ的期望价值,即价值函数:
)是一个随机变量,表示沿着一个状态轨迹所观察到的折扣奖励之和。标准RL算法估算Zπ的期望价值,即价值函数:
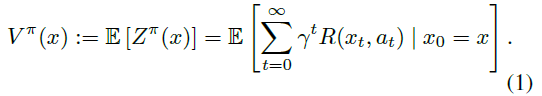
同样,许多RL算法会估算动作-价值函数:

关于Qπ的ε-贪婪策略均匀随机地以概率ε选择动作,否则根据argmaxa Qπ(x, a)进行选择。
在分布RL中,回报的分布(即Zπ的概率定律)起着核心作用并取代了价值函数。我们将通过其随机变量来指代价值分布。当我们说价值函数是价值分布的均值时,指的是价值函数是在价值分布的所有内在随机性源(Goldstein, Misra and Courtage, 1981)上得到的期望价值。这应该突出表明,价值分布并不是设计来捕获价值函数估计中的不确定性(Dearden, Friedman and Russell, 1998; Engel, Mannor and Meir, 2005),而是参数不确定性,而在于MDP固有的回报。
时序差分(TD)方法通过使用Bellman算子进行动态编程来逐步提高Qπ的估计价值,从而显著加快了学习过程(Bellman, 1957):

类似地,可以使用分布Bellman算子(Bellemare, Dabney and Munos, 2017)通过动态编程来计算价值分布:

其中![]() 表示概率密度相等,即随机变量Y根据与U相同的密度分布。
表示概率密度相等,即随机变量Y根据与U相同的密度分布。
C51算法使用离散分布对Zπ(x, a)进行建模,该离散分布支持在固定位置z1 ≤ … ≤ zN的“梳子”上,且均匀分布在预定间隔上。该分布的参数是与每个位置zi相关联的概率qi,用对数表示。在给定当前价值分布的情况下,C51算法应用投影步骤将目标TπZ映射到其有限元支持上,然后执行Kullback-Leibler(KL)最小化步骤(请参见图1)。C51在Atari 2600游戏上达到了最先进的性能,但与Bellemare,Dabney和Munos(2017)的理论结果明显脱节。现在,我们先回顾这些结果,然后再将它们推广到近似分布的情况。
The Wasserstein Metric
对于p∈[1, ∞],p-Wasserstein度量Wp,这被称为Mallows度量(Bickel and Freedman, 1981),当p=1时,这被称为或陆地移动距离(EMD)(Levina and Bickel, 2001),是分布之间的积分概率度量。p-Wasserstein距离的特征是逆累积分布函数(逆CDF)的Lp度量(Müller, 1997)。也就是说,分布U和Y之间的p-Wasserstein度量由下式给出:1
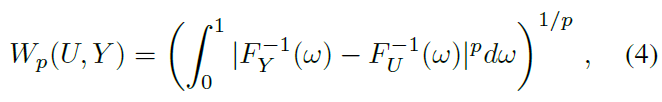
其中,对于随机变量Y,Y的逆CDF![]() 定义为:
定义为:
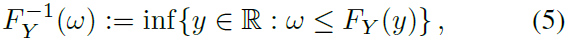
其中FY(y) = Pr(Y≤y)是Y的CDF。图2将1-Wasserstein距离说明为两个CDF之间的面积。
最近,Wasserstein度量具有尊重结果之间潜在的度量距离的吸引人的特性,因此成为越来越多的研究重点(Arjovsky, Chintala and Bottou, 2017; Bellemare et al., 2017)。与Kullback-Leibler散度不同,Wasserstein度量是一个真实的概率度量,它同时考虑了各种结果事件的概率以及两者之间的距离。这些特性使Wasserstein非常适合于结果的潜在相似性比精确匹配可能性更重要的领域。
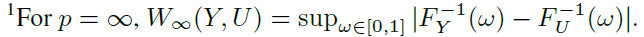
The convergence of Distributional Bellman Operator
在分布RL的上下文中,令Z为具有有限矩的动作-价值分布的空间:
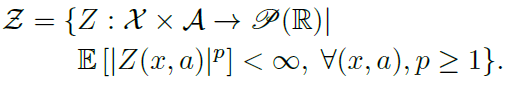
然后,对于两个动作-价值分布Z1, Z2∈Z,我们将使用由(Bellemare, Dabney and Munos, 2017)引入的Wasserstein度量的最大形式:
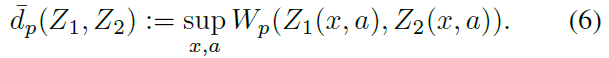
结果表明,![]() 是衡量价值分布的度量。此外,分布Bellman算子Tπ是
是衡量价值分布的度量。此外,分布Bellman算子Tπ是![]() 的压缩,我们现在回想一下结果。
的压缩,我们现在回想一下结果。


在实际情况下,此问题变得很突出,在这种情况下,价值分布必须近似。至关重要的是,不能保证C51算法会最小化任何p-Wasserstein度量。分布RL中的理论与实践之间的差距并不限于C51。Morimura et al.(2010)使用高斯或拉普拉斯分布的均值和尺度对价值分布进行参数化,并最小化目标TπZ和预测Z之间的KL散度。他们证明以这种方式学习到的价值分布足以执行风险敏感的Q-Learning。但是,从他们的方法得出的任何理论保证都只能是渐近的。Bellman算子充其量是KL散度的非拓展。
Approximately Minimizing Wasserstein
回想一下,C51通过附加变量(参数化)概率q1, …, qN到固定位置z1 ≤ … ≤ zN来近似表示每个状态的分布。我们的方法是通过考虑固定概率但位置可变来“转置”此参数化。具体来说,我们采用统一的权重,因此对于每个i=1, …, N,qi=1/N。
实际上,我们的新近似方法旨在估计目标分布的分位数。因此,我们将其称为分位数分布,并令ZQ为固定N的分位数分布的空间。我们将与该分布相关的累积概率(即CDF所采用的离散价值)表示为τ1, …, τN,因此对于i=1, …, N,![]() 。我们还将τ0=0以简化表示法。
。我们还将τ0=0以简化表示法。

与原始参数化相比,参数化分位数分布的好处是三个方面的。首先,(1)我们不受限于支持的预定范围或均匀的分辨率,当各状态的回报范围差异很大时,有可能导致更准确的预测。(2)这还使我们消除了C51中存在的笨拙的投影步骤,因为没有脱节支持的问题。当将算法应用于新任务时,这些共同消除了对关于回报分布范围的领域知识的需求。最后,(3)这种重参数化使我们能够将Wasserstein损失降到最低,而不会受到有偏梯度的影响,特别是使用分位数回归。
The Quantile Approximation
众所周知,在强化学习中,函数逼近的使用可能会导致学习过程不稳定(Tsitsiklis and Van Roy, 1997)。具体地说,投影到近似空间上的Bellman更新可能不再是压缩。在我们的案例中,我们分析了分布Bellman更新,投影到参数化的分位数分布上,并证明组合算子是一个压缩。
Quantile Projection 我们感兴趣的是量化任意价值![]() 分布在
分布在![]() 上的投影,即:
上的投影,即:

令Y为有界第一矩的分布,U为N Diracs上的均匀分布,如(7)所示,其支持为![]() 。然后,
。然后,
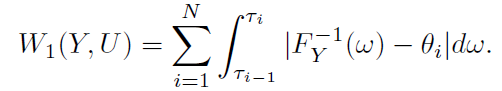

2由于篇幅所限,我们保留附录的证明。
Quantile Regression
定理1的原始证明仅表明存在有偏梯度的分布。作为结果,我们可能希望分位数参数化导致无偏梯度。不幸的是,事实并非如此。
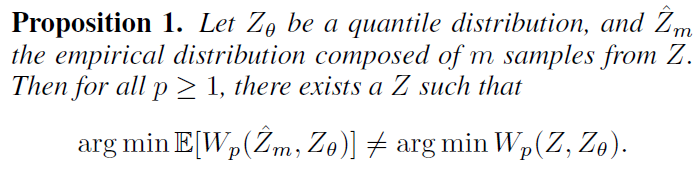
但是,有一种方法在经济学中比机器学习更广泛地用于分位数函数的无偏随机逼近。分位数回归和条件分位数回归分别是逼近分布和条件分布的分位数函数的方法(Koenker, 2005)。这些方法已被用于结局具有内在随机性的各种环境中(Koenker and Hallock, 2001);从食品支出到家庭收入的函数(Engel, 1857),到研究经济模型中的风险价值(Taylor, 1999)。
对于分位数τ∈[0, 1],分位数回归损失是一个非对称凸损失函数,该函数惩罚权重为τ的高估误差和权重为1-τ的低估误差。对于分布Z和给定分位数τ,分位数函数![]() 的价值可以表征为分位数回归损失的最小值:
的价值可以表征为分位数回归损失的最小值:
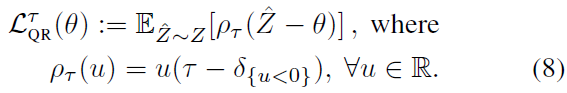
更一般地,通过引理2,我们对W1(Z, Zθ)最小化{θ1, …, θN}的值,这些值最小化以下目标:
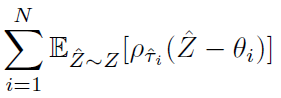
特别是,这种损失会产生无偏的样本梯度。作为结果,通过随机梯度下降,我们可以找到最小化{θ1, …, θN}的值。
Quantile Huber Loss 分位数回归损失在零处不平滑;当u → 0+时,公式8的梯度保持恒定。我们假设使用非线性函数逼近会限制性能。为此,我们还考虑了改进的分位数损失,称为分位数Huber损失。3这种分位数回归损失在零附近的区间[-κ, κ]充当不对称平方损失,并还原到此间隔之外的标准分位数损失。
Huber损失由(Huber, 1964)给出,

分位数Huber损失就是Huber损失的不对称变体,
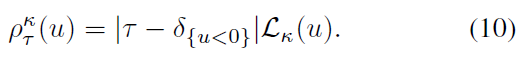
为了简化符号,我们将设置![]() ,即它将还原为标准的分位数回归损失。
,即它将还原为标准的分位数回归损失。
3我们的分位数Huber损失与Aravkin et al.(2014)的损失有关,但与其有所不同。
Combining Projection and Bellman Update
现在,我们可以证明我们的主要结果,该结果表明分位数回归所隐含的投影与Bellman算子的组合是一个压缩。结果是∞-Wasserstein度量,即两个CDF之间最大间隙的大小。

Distributional RL using Quantile Regression
现在,我们可以形成一个与我们的理论结果相符的完整算法,用于分布RL。也就是说,用引理2定义的分位数中点集上的参数化分位数分布来近似价值分布。然后,使用分位数回归来训练位置参数(公式8)。
Quantile Regression Temporal Difference Learning
回顾用于评估策略π的标准TD更新,

TD允许我们随着π用单个无偏样本来更新估计价值函数。分位数回归还允许我们通过观察样本y ~ Y(x),并使等式8最小化来改进某些目标分布Y(x)的分位数函数的估计。
此外,我们已经表明,通过为τ∈(0, 1)的精心选择的价值估计分位数函数,我们可以获得与原始值(引理2)的1-Wasserstein距离最小的近似。最后,我们可以将其与分布Bellman算子结合起来,以给出分位数回归的目标分布。这为我们提供了分位数回归时序差分学习(QRTD)算法,该算法用更新进行简单地归纳,

其中Zθ是(7)中的分位数分布,θi(x)是状态x下![]() 的估计价值。重要的是要注意,此更新针对
的估计价值。重要的是要注意,此更新针对![]() 的每个价值,并针对来自下一个状态价值分布的单个样本进行定义。通常,最好绘制z' ~ Z(x')的许多样本,并尽量减少期望更新。在这种情况下,我们在实践中使用的自然方法是为(θi(x), θj(x'))的所有对计算更新。接下来,我们转向控制算法并使用非线性函数逼近。
的每个价值,并针对来自下一个状态价值分布的单个样本进行定义。通常,最好绘制z' ~ Z(x')的许多样本,并尽量减少期望更新。在这种情况下,我们在实践中使用的自然方法是为(θi(x), θj(x'))的所有对计算更新。接下来,我们转向控制算法并使用非线性函数逼近。
Quantile Regression DQN
Q-Learning是一种脱离策略的强化学习算法,使用Bellman最优算子建立围绕直接学习最优动作-价值函数(Watkins and Dayan, 1992),

它的分布变量是估计状态-动作价值分布并应用分布Bellman最优算子,

特别注意,用于下一个状态的动作是相对于下一个状态-动作价值分布均值的贪婪动作。
对于一个具体的算法,我们将基于DQN架构(Mnih et al., 2015),我们关注于形成DQN的分布版本所需的最小更改。具体来说,我们需要对DQN进行三处修改。首先,我们使用与DQN几乎相同的神经网络架构,只是将输出层更改为大小|A| x N,其中N是给出分位数目标数量的超参数。其次,我们用DQN4代替Huber损失,![]() ,并用分位数Huber损失(算法1给出的全损失)。最后,我们用Adam(Kingma and Ba, 2015)代替RMSProp(Tieleman and Hinton, 2012)。我们称这种新算法为分位数回归DQN(QR-DQN)。
,并用分位数Huber损失(算法1给出的全损失)。最后,我们用Adam(Kingma and Ba, 2015)代替RMSProp(Tieleman and Hinton, 2012)。我们称这种新算法为分位数回归DQN(QR-DQN)。

与C51不同,QR-DQN不需要投影到近似分布的支持上,而是可以任意扩展或压缩价值以覆盖回报价值的真实范围。另一个优点是,这意味着QR-DQN不需要附加的超参数即可提供C51所需的支持范围。DQN不共享的QR-DQN的唯一的额外超参数是分位数数量N,它控制着我们以何种分辨率近似价值分布。随着我们增加N,QR-DQN从DQN变为越来越能够估计价值分布的上下分位数。它变得越来越有能力区分回报的累积分布两端的低概率事件。
4DQN使用平方误差的梯度裁剪,使其等于κ=1的Huber损失。
Experimental Results
在引言中,我们声称学习回报分布优于仅学习价值函数。在本节中,我们将凭经验验证所提出的分布强化学习算法:(1)了解回报的真实分布;(2)在训练过程中显示出更高的鲁棒性;(3)与基准算法相比,大大提高了样本复杂度和最终性能。
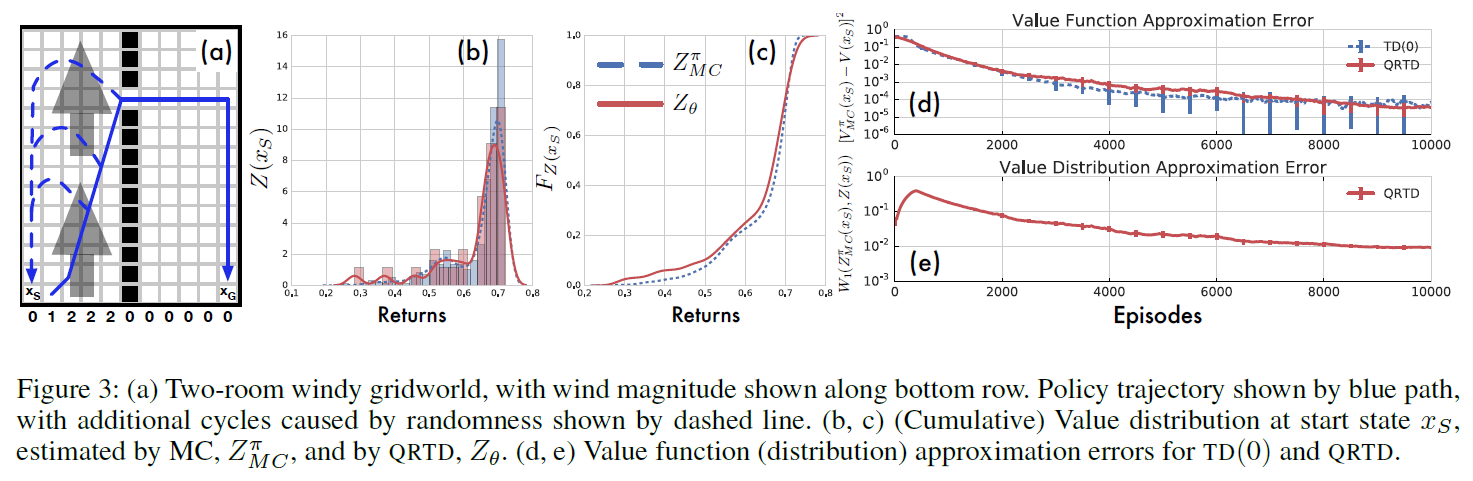
Value Distribution Approximation Error 我们通过证明QRTD实际上学习了一个近似价值分布来开始我们的实验结果,使得该分布到回报的真实分布的1-Wasserstein最小化。尽管我们的理论结果已经建立了前者到后者的收敛,但是经验性能有助于完善我们的理解。
我们使用经典的有风gridworld域的变体(Sutton and Barto, 1998),将其修改为在转换中具有两个空间和随机性。图3(a)显示了我们版本的域,其中我们结合了转换随机性,风和门口,以便在第一个空间中的任何位置时,在回报上产生多峰分布。每个状态转换都有沿随机方向移动的概率为0.1,否则该转换会受到风将智能体向北移动的影响。奖励函数为零,直到达到目标状态xG为止,该状态终止eposide并给出奖励1.0。折扣因子是γ=0.99。
我们通过执行1K蒙特卡洛(MC)部署并将观察到的回报记录为经验分布,来计算每个状态下通过策略迭代学习到的最优策略π的真实价值分布,如图3(b)所示。接下来,我们同时运行TD(0)和QRTD进行10K个eposide。每个eposide都以指定的开始状态(xS)开始。两种算法的初始学习率α=0.1。对于QRTD,我们使用N=32,每2K个episode减少一半的α。
令![]() 为从初始状态xS返回的MC估计分布,类似地,其均值为
为从初始状态xS返回的MC估计分布,类似地,其均值为![]() 。在图3中,我们显示了两种算法在xS时相对于episode数量的近似误差。在(d)中我们评估了TD(0)和QRTD的平方误差,
。在图3中,我们显示了两种算法在xS时相对于episode数量的近似误差。在(d)中我们评估了TD(0)和QRTD的平方误差,![]() ,在(e)中我们显示了QRTD的1-Wasserstein度量,
,在(e)中我们显示了QRTD的1-Wasserstein度量,![]() ,其中V(xS)和Z(xS)是在算法估算的状态xS下的期望回报和价值分布。如预期的那样,两种算法的均值均正确收敛,QRTD最小化到
,其中V(xS)和Z(xS)是在算法估算的状态xS下的期望回报和价值分布。如预期的那样,两种算法的均值均正确收敛,QRTD最小化到![]() 的1-Wasserstein距离。
的1-Wasserstein距离。
Evaluation on Atari 2600
现在,我们提供的实验结果证明了与C51方法相比,最大限度地减小端到端Wasserstein度量的实际优势。我们使用了Arcade学习环境(ALE)的57个Atari 2600游戏(Bellemare et al., 2013)。C51和QR-DQN都建立在标准DQN结构上,我们希望双方都将从DQN的最新改进中受益,例如对偶结构(Wang et al., 2016)和优先回放(Schaul et al., 2016)。然而,在我们的评估中,我们比较了没有这些附加的C51和QR-DQN的纯粹版本。我们给出了严格分位数损失,κ=0(QR-DQN-0)和Huber分位数损失,κ=1(QR-DQN-1)的结果。
我们对五个训练游戏进行了超参数调整,并使用这些最优设置(α=0.00005,εADAM=0.01/32和N=200)对整个57个游戏进行了评估。5正如DQN,我们在计算分布Bellman更新时使用目标网络。我们还允许ε以与DQN中相同的速率进行衰减,但衰减至较低价值0.01,这在最近工作中所常见(Bellemare, Dabney and Munos, 2017; Wang et al., 2016; van Hasselt, Guez and Silver, 2016)。
我们的训练程序遵循Mnih et al.(2015)的方法,并且我们根据两种评估协议展示了结果:最优智能体性能和在线性能。在这两种评估协议中,我们都考虑了57种Atari 2600游戏的性能,并将原始分数转换为人为化分数(van Hasselt, Guez and Silver, 2016)。
5我们遍历α于(10-3, 5 x 10-4, 10-4, 5 x 10-5, 10-5);εADAM于(0.01/32, 0.005/32, 0.001/32);N于(10, 50, 100, 200)
Best agent performance 为了提供与现有工作相当的结果,我们报告了最佳智能体协议下的测试评估结果。每一百万个训练帧,学习就会冻结,并在记录平均回报的同时,对智能体评估50万个帧。评估eposide始于最多30次随机无操作(Mnih et al., 2015),智能体使用较低的探索率(ε=0.001)。随着训练的进行,我们会跟踪迄今为止取得的最优智能体性能。
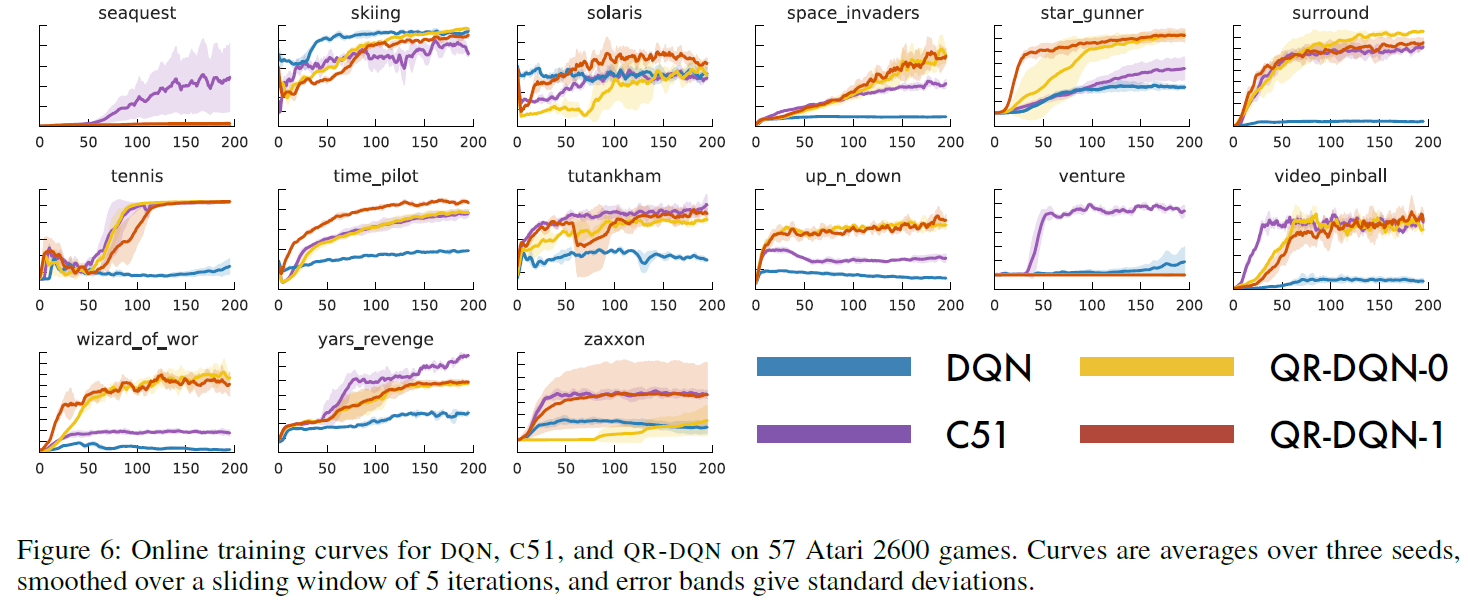
表1给出了针对QR-DQN,C51,DQN,双重DQN(van Hasselt, Guez and Silver, 2016),优先回放(Schaul et al., 2016)和对偶架构(Wang et al., 2016)经过2亿帧训练后的最优智能体性能。我们发现QR-DQN在人为归一化分数均值和中位数方面优于之前所有的智能体。

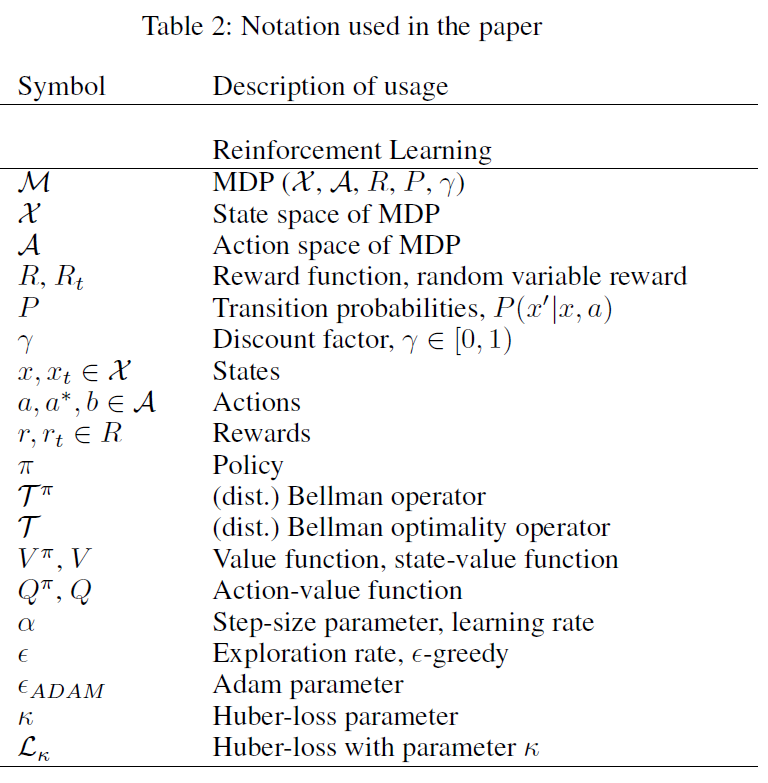
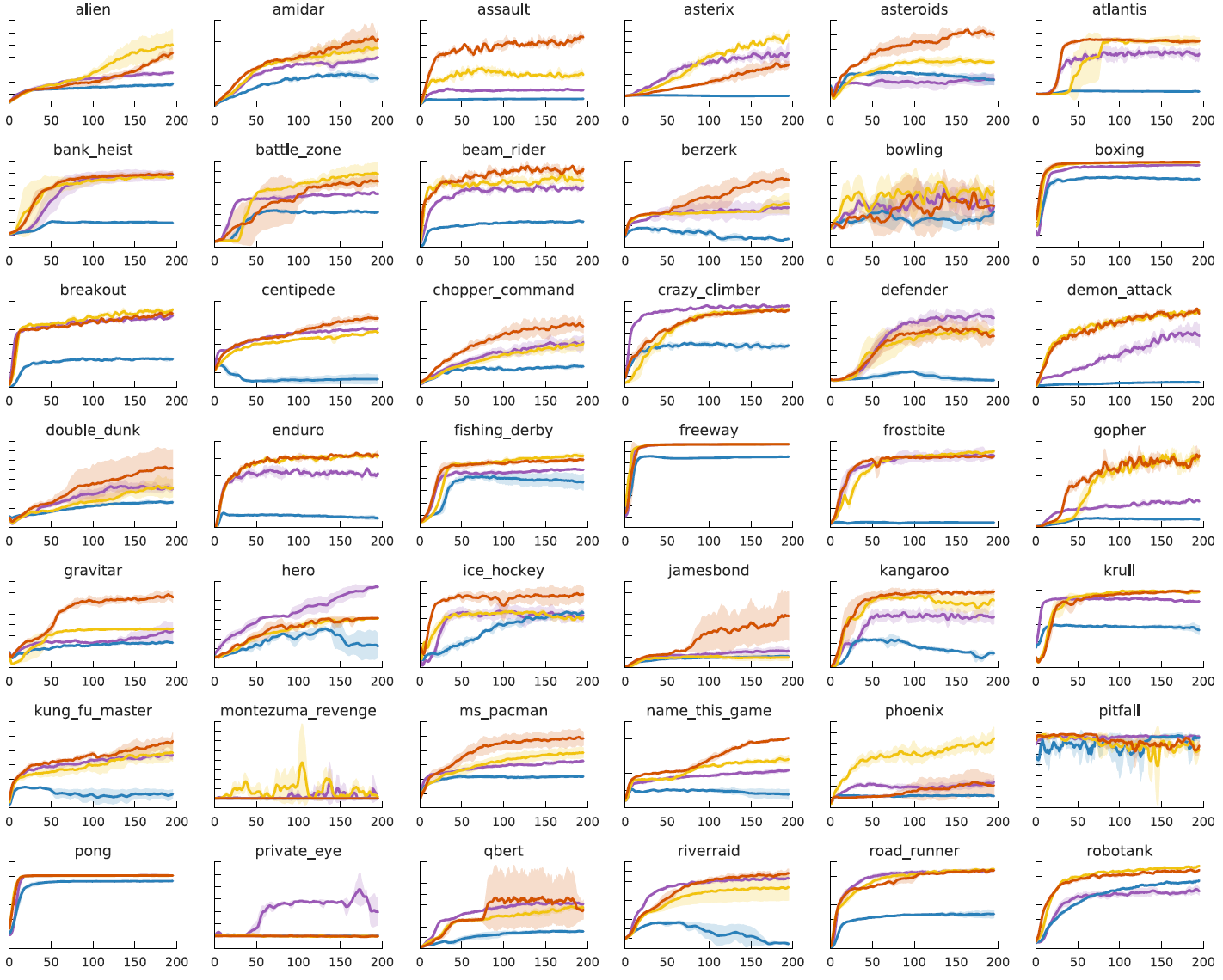
Online performance 在此评估协议(图4)中,我们跟踪每次测试(左)和训练(右)迭代期间获得的平均回报。对于测试性能,我们为每种算法使用一个种子,但是显示了在线性能,没有任何形式的提前停止。对于训练表现,价值是三个种子的平均值。我们不只是报告中位数的表现,而是查看整个游戏中人为归一化分数的分布。每个块代表固定百分比(10th、20th、30th、40th和50th)的分数分布。较高的百分比显示出相似的趋势,但为清晰起见在此省略,因为它们的比例使信息量较低的下半部分相形见绌。
由此,我们可以推断出一些有趣的结果。(1)在学习初期,至少在10%的游戏中,大多数算法的性能都比随机算法差。(2)QRTD在优先回放方面对样本复杂度做出了类似的改进,同时还提高了最终性能。(3)即使在2亿帧的情况下,也有10%的游戏中所有算法的使用率不到人为的10%。最后一点特别向我们表明,我们最近的所有进步仍然受到Atari 2600游戏的一小部分的严重限制。

Conclusions
在强化学习中,回报分布的重要性已经被(重新)发现并被强调很多次。在Bellemare, Dabney和Munos(2017)中,这一想法又向前迈进了一步,并被认为是近似强化学习的核心部分。但是,此文悬而未决的问题是,是否存在一种可以弥补Wasserstein度量理论与实际问题之间差距的算法。
在本文中,我们用理论贡献和一种新算法填补了这一空白,该算法在Atari 2600中达到了最先进的性能。未来的工作还有许多有希望的方向。最令人兴奋的是扩大动作-价值分布使之成为更丰富的策略类别的希望。我们提到了此类策略的一些示例,这些示例通常用于对风险敏感的决策中。但是,还有更多可能的决策策略将动作-价值分布作为一个整体来考虑。
此外,QR-DQN可能会受益于近年来对DQN所做的改进。例如,由于损失函数和Bellman算子的相似性,我们可能期望QR-DQN遭受与双重DQN旨在解决的相似的高估偏差(van Hasselt, Guez and Silver, 2016)。自然而然的下一步是将QR-DQN与表1中的非分布方法相结合。
Appendix
Proofs






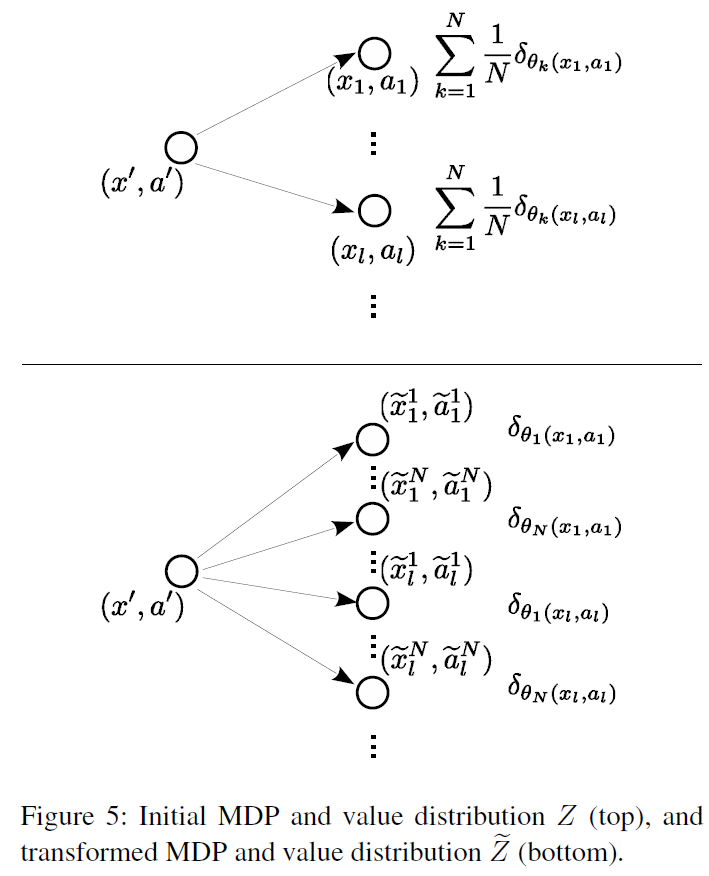
Supporting results




Further theoretical results


Notation