郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布! 以下是对本文关键部分的摘抄翻译,详情请参见原文。

Abstract
我们展示了如何构造各种“trapdoor”密码工具,假设标准格问题的最坏硬度(例如在最短的非零向量上近似于小因子)。应用包括带预图像采样的trapdoor函数,简单高效的“哈希签名”数字签名方案、通用可组合的不经意传输和基于身份的加密。
我们构造的一个核心技术组件是一个有效的算法,该算法在给定任意格的基础上,从类高斯概率分布中采样格点,其标准差本质上是基中最长向量的长度。特别地,关键的安全特性是算法的输出分布不受给定基的特定几何结构的影响。
1 Introduction
自从Ajtai[Ajt96]的开创性工作将格问题的平均复杂度与它们的最坏复杂度联系起来之后,在最坏情况的格假设下,基于密码的安全性(需要随机选择的密钥的安全性)一直是一个有趣且卓有成效的努力。除了其独特的理论利基外,基于格的方案还具有许多优点:第一,它们的渐近效率和简单性(通常只需要对小整数进行线性运算);第二,它们迄今为止对量子算法进行密码分析的阻力(与基于因子分解或离散对数的方案相反);第三,基于格的方案保证它们的随机实例是“尽可能困难的”。
迄今为止,此类原语的已知构造主要限于单向和抗冲突哈希函数[Ajt96,GGH96,CN97、Mic04,MR07]和公钥加密[AD97,Reg04,Reg05]。特别值得注意的是,即使在随机预言模型(random oracle model)中,也缺乏任何具有其他基于格的原语的简单高效的数字签名的“直接”构造。(Goldreich、Goldwasser和Halevi的早期签名方案[GGH97]与某个格问题直接相关,但缺乏安全性证明,最近,Nguyen和Regev[NR06]展示了如何从签名(随机消息)的转录本中完全恢复密钥。我们将在下面详细讨论GGH计划。)
基于格的强密码工具(如选择密文安全加密[PW07])的构造有了一些新的进展。但是,尽管密码学中格的研究取得了许多进展,但是如何实现一些很久以前建立在其他数论问题上的概念,如与因式分解有关的概念,仍然是个未知数,标准差实质上是基中最长向量的长度。特别地,关键的安全特性是算法的输出分布不受给定基的特定几何结构的影响。
1.1 Overview of Results and Techniques
我们在这项工作中的主要论点是,格允许自然和固有的“trapdoor”,它们具有许多有用的密码应用。至少可以追溯到GGH的提议[GGH97],人们直觉上认为,格的短基可以充当这样一个trapdoor。我们的主要贡献是展示如何在理论上合理和安全地使用一个trapdoor基。
作为一个基本的工具,我们首先构造一个具有一些特殊性质的trapdoor函数集合。函数是多对一的(即每个输出值都有多个预图像),trapdoor逆算法在适当的分布下从所有预图像中进行采样。在此基础上,我们展示了几种更先进的密码工具的有效实现,包括签名方案、通用可组合的不经意传输以及基于身份的加密。
所有这些结果的核心技术是一种有效的算法,在给定一个适当长度的基(甚至仅仅是一个完整的秩集)的情况下,从任意格上的类高斯概率分布中“遗忘”地采样。这种技术还产生了更简单和(稍微)更紧的最坏情况/平均情况连接的格问题,并可能在复杂理论和密码学中有附加的应用。
1.1.1 Gaussian Sampling Algorithm
因为它是我们密码结果的主要基础,所以我们从我们的抽样算法的总结开始。在给定任意n维格Λ的基B包含于Rn(甚至是全秩集S包含于Λ)的情况下,该算法在类高斯概率分布下随机选择一个格向量,其标准差实质上是B(或S)中最长向量的长度。格上的这种离散的高斯分布在数学中被用来证明格的严格的“转移定理”[Ban93/Ban95],并且最近在证明格问题的计算复杂性[AR03,AR05,Pei07]中特别有用,特别是它们最坏情况/平均情况的连接(例如,[Reg04,MR07,Reg05])。然而,到目前为止,离散高斯函数主要被用作分析工具,而不是算法工具。
采样算法也可以看作是一个随机解码器,在给定一些短的格向量作为“建议”的情况下,输出一个相对接近任何给定目标点t∈Rn的格向量。解码器的关键特性是其输出分布仅取决于建议向量的长度,否则不受其特定几何结构的影响。这将是我们加密应用程序中的一个关键安全属性。
算法本身实际上是Babai的“nearest-plane”(最近平面)算法[Bab86]的一个简单随机变量,只有一个小的差异。算法不总是选择最近的平面,而是选择一个特定的平面,其概率取决于它与目标点的距离。结果表明,这种简单的变化导致输出分布在统计上接近离散高斯分布,尽管分析是非平凡的,并且关键地使用了Micciancio和Regev[MR07]引入的平滑参数的概念。第三章给出了全部细节。
1.1.2 Cryptographic Constructions
对于我们所有的密码构造,我们需要为随机格生成一个“困难的”公共基Λ,以及Λ的一个短的私有基,这将用作采样算法的建议。我们首选的方法是出于Ajtai[Ajt99],他描述了一种生成此类基的方法,使得公共基具有最坏情况下的困难性。(据我们所知,我们的结果是在密码学或其他领域首次使用Ajtai的生成器。)
带预图像采样的trapdoor函数:我们的高级加密工具的基本对象是单向(同时也是抗冲突)trapdoor函数的集合。非常不正式地,计算公共函数f相当于“均匀随机”地选择格点v∈Λ,并通过一些短误差项e对其进行扰动,从而产生一个点y=v+e。找到y的原像对应于将其解码到足够近的格点v'∈Λ(不一定是原始的v)。这是很容易使用我们的采样算法与trapdoor,但否则应该很难(对于特定的分布Λ和y)。
我们的trapdoor函数在密码应用程序中有两个重要的安全属性。首先,输入(误差项e)从标准差相对较小的高斯分布中采样,并且在该分布下,输出y在统计上接近于在该范围内的均匀性。这就把逆问题等同于对给定公共基的均匀随机点进行解码,我们可以对其显示最坏情况的困难性。其次,trapdoor的逆算法不仅可以找到y的任意一个原像,而且可以使用我们的离散高斯采样算法从y的所有原像中(在适当的条件分布下)进行实际采样。换言之,逆变器从高斯输入分布中对输入e进行采样,条件是f(e) = y。这两个特性共同表明,有两种(几乎)选择对(e, y = f(e))的等效方法:从输入分布中选择e并计算y = f(e),或随机均匀地选择y并从f-1(y)中采样得到e。正如我们将看到的,这使得我们的trapdoor函数在某些应用中和trapdoor置换"一样好"。
关于随机格的进一步讨论,硬解码问题,以及我们的trapdoor函数的全部细节,见第四章。
签名方案:文献中有几种(相对有效的)基于trapdoor置换的数字签名方案:全域类哈希方案[DH76,BR93,BR96,Cor02]遵循所谓的“hash-and-sign paradigm”(哈希与签名范式),并在随机预言模型(random oracle model)中进行了安全分析,且Bellare和Michali的方案[BM92]在标准模型上是安全的。
我们证明,上述所有基于置换的签名方案,使用带有预图像采样的trapdoor函数,能够同样好地进行实例化,并将其安全性分析保留在各自的模型中(尽管在处理同一消息上的多个查询时可能会出现细微差别)。事实上,我们可以使用函数的抗碰撞特性来演示严格的安全性降低,而不仅仅是它们的单向性。
具体地说,我们的hash-and-sign签名与原始的(但不安全的)GGH方案及其变体[GGH97,HHGP+03]非常相似:非正式地,消息被散列到空间中的一个随机点,其签名本质上是一个附近的格点,这是使用短基找到的。我们的方案有两个主要区别:第一,它们基于具有最坏情况困难性的随机格;第二,更重要的是,签名是由随机解码算法生成的,其输出分布不受trapdoor基的特定几何结构的影响。(GGH最初的提议是不安全的,正是因为它的签名泄露了关于私有基的“形状”的信息,允许完全密钥恢复[NR06]。)
第五章构造并分析了签名方案。
有效的普遍可组合的不经意转移:我们的下一个应用是围绕一个基于错误学习(learning with error, LWE)问题的regev密码系统[Reg05]。我们演示了一个trapdoor,它适用于一个优化版本的系统,在这个系统中,所有参与方都相对于某个共享随机格生成它们的公钥。
这个trapdoor的第一个应用是普遍可组合的不经意转移,这是Peikert等人的一个并发工作的主题[PVM07]。这项工作的中心研究对象被称为消息有损(或“凌乱”)公钥,其定义属性是在这种密钥下生成的密文不携带(统计上)关于加密消息的信息。
以前关于基于格的加密的工作[AD97,REG04,REG05]使用概率参数来表明混乱的密钥非常密集。在这项工作中,我们给出了一个在(一个微小的变种)Regev's密码系统中显式的几何描述凌乱的密钥。从本质上讲,如果公钥在与共享格相邻之后,该格的最小距离仍然较大,则该公钥是混乱的。然后,我们展示了如何识别这些密钥,使用我们的高斯采样算法有效地实现了算法的预处理步骤,该算法根据Aharonov和Regev[AR05]识别远离给定格的点。
第六章将进一步详细描述用于Regev密码系统的trapdoor。
基于身份的加密:Shamir[Sha84]首先提出的基于身份的加密(IBE)允许任意字符串作为密码系统中的公钥。到目前为止,IBE是在随机预言模型中的二次剩余(QR)假设下,或在标准模型中的“交互”QR假设[Coc01,BGH07]下,使用具有双线性对的群(例如[BF03,BB04,Wat05])来实现的。
我们的最终应用是在随机预言模型中基于LWE的有效IBE,或者在标准模型中基于LWE困难性的交互假设下。尽管在Regev's基于LWE的密码系统中可以从公钥(使用trapdoor)中提取密钥,但是获得IBE仍然不是完全直截了当的。本质上,问题是格式良好的公钥是指数稀疏的,因为它们只包含非常接近共享格的点。因此,很难看到哈希函数或随机预言如何将身份映射到有效的公钥。我们通过构造一个“对偶”的Regev's密码系统来解决这个问题,其中密钥生成和加密算法被有效地交换。在得到的系统中,空间中的每个点都是一个有效的公钥,它有许多等价的密钥,这些密钥仅仅是与公钥足够接近的格点。
由于使用trapdoor提取密钥,我们的IBE在结构上与基于QR的IBE最为相似[Coc01,BGH07]。它是非常有效的,至少在渐近意义上是这样的:对于˜Θ(n)位消息(其中n是安全参数),加密和解密的摊余运行时间仅为每个加密位的˜O(n)位操作。密文展开式是O(1),甚至可以在LWE上的足够强(但仍然是多项式)假设下任意接近1。我们系统的一个可能的缺点是,主公钥和单个密钥都是˜O(n2)位。
双重密码体制和IBE的构造见第七章。
1.2 Assumptions
我们的trapdoor函数和签名是建立在随机格上平均情况下的"绝对距离"解码问题上的。我们的“类加密”原语,即不经意的传输和基于身份的加密,是建立在Regev[Reg05]定义的平均情况下的错误学习(LWE)问题上的。LWE可以看作是某类随机格上的一个“唯一解码”问题,是研究得很好的learning parity with noise问题的一个推广(到更大的模),它被认为是困难的,在密码学中有许多应用(如[BKW03,HB01,JW05,KS06])。
在最坏的情况下,如果标准格问题(如最短向量问题)难以近似于格维数内的小多项式因子,则上述两个解码问题在平均情况下都是困难的。然而,LWE的缩小是量子的[Reg05],即,如果某些格问题在量子算法的最坏情况下是困难的,则LWE是困难的。鉴于目前的技术水平,有必要对类加密原语进行更强有力的假设,因为对于一般格,没有基于经典最坏情况困难性的已知密码系统。
对于我们的方案中的格问题,最有名的经典(和量子)算法需要时间和空间指数在格的尺寸,以及最有名的多项式时间算法提供指数宽松近似。
1.3 Related Work
使用完全不同的技术,Peikert和Waters[PW07]构建了一个完全互补的基于格问题(其一)的单射trapdoor函数集合。他们的TDFs基于LWE的困难性,而我们的TDFs完全基于经典的最坏情况下的困难性。他们的TDFs是指数稀疏图像的单射,而我们的TDFs是多对一的和满射的。他们的TDFs意味着选择密文安全加密,但稀疏的图像似乎使他们不太适合像签名方案和IBE这样的应用。最后,从纯美学的角度来看,我们的trapdoor函数更直接地对应于格上的“自然”解码问题。
如上所述,Peikert、Vaikuntanathan和Waters[PVW07]利用我们的trapdoor检测凌乱的密钥,从最坏情况的格假设(其一)构建了高效且通用的可组合不经意传输协议。这项工作早于此,并为我们的trapdoor技术和高斯采样算法提供了动力。
在保密通信中,Lyubashevsky指出,我们用于高斯采样的随机最近平面算法本质上是Klein[Kle00]提出的用于解决不同问题的算法。Klein考虑最近向量问题的一个限制变量,其中目标点被保证“异常接近”格。他的分析表明,在这样的条件下,该算法以显著的概率来输出最近的格向量。我们的贡献是分析了该算法对于任意目标点的整个输出分布,这表明该分布不受建议基的影响。
2 Preliminaries
2.1 Notation


2.2 Standard Definitions

2.3 Lattices

格的具体定义可参见《Better Key Sizes (and Attacks) for LWE-Based Encryption》中的Preliminaries部分,Λ*为Λ的对偶格,span(Λ)表示Λ的生成子空间,<x, v>表示两个向量之间的点积。λ1(Λ)暗含l2范数,而λ1∞(Λ)暗含l∞范数。
2.4 Gaussians on Lattices
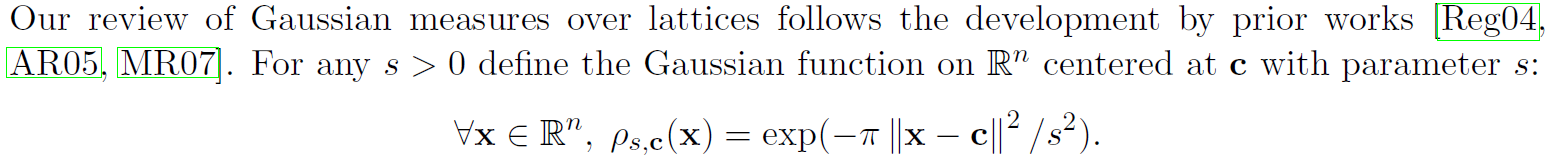



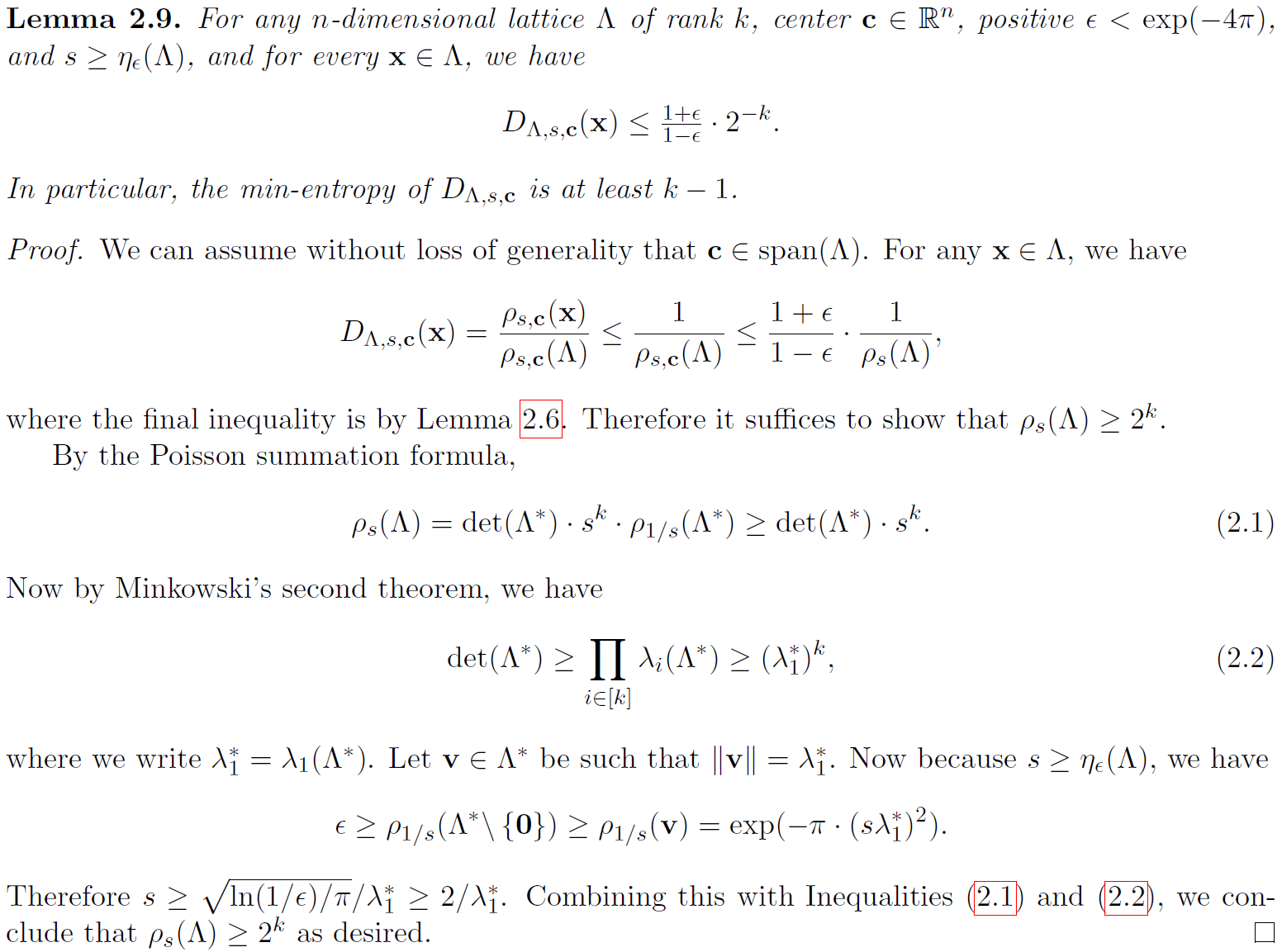
2.5 Learning with Error


3 Sampling from Discrete Gaussians
在这里,我们展示了如何有效地从离散高斯概率分布DΛ,s,c中采样,给定以s为界的任何长度基(或全秩集)。作为第一次尝试,我们可以考虑首先从连续高斯分布中采样,然后使用短基将采样点“舍入”到附近格点的算法。事实上,Regev使用了这个精确的策略来进行缩减的“bootstrapping”步骤[Reg05],并使用LLL-reduced基和指数大于基长度的高斯参数s。不幸的是,当s是基长的较小倍数(例如poly(n))时,还不清楚该策略是否同样有效。问题是,在映射(通过舍入)到特定格点的空间区域内,连续高斯分布的密度函数可能显著变化。这使得分析舍入方案下分配给每个格点的总概率质量,并将其与期望的离散高斯分布进行比较变得困难。
下面的采样算法完全避免了连续高斯分布,并且以一种紧凑的方式从格中“直接”采样。它可以看作是Babai's最近平面算法的一个随机版本[Bab86],该算法不总是选择最近的平面,而是随机选择一个平面,其概率与它与目标点的距离有关。本节的其余部分将致力于正式定义和分析采样算法。
3.1 Sampling Integers

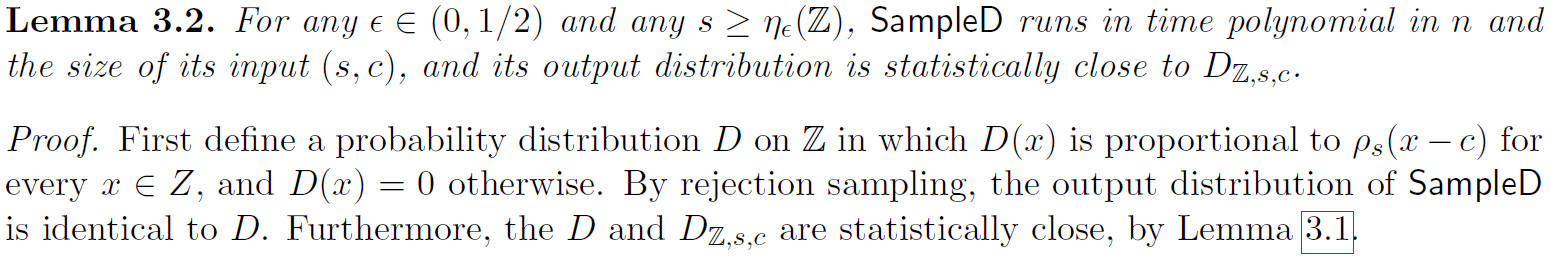

我们首先开发了一个核心子程序,它从特定一维格上的离散高斯分布(即整数Z)中采样。该子程序将依赖于分布的尾不等式。
从DZ,s,c(对于足够大的s)中有效地采样有几种可能的方法;用标准的拒绝采样方法最容易描述工作让t(n) ≥ w(sqrt(log n))是一个固定的函数。算法SampleD的工作原理如下:在输入 (s, c) 和(隐式地)安全参数n上,随机选择一个整数x ← Z = Z ∩ [c - s · t, c + s · t],然后以概率ρs(x - c),输出x,否则重复。
我们现在分析运行时间。每次SampleD的迭代从Z中选取一个均匀随机整数x。所选整数x落入集合Z ∩ [c - s, c + s]中的概率至少为 (2s - 1) / (2s · t) ≥ 1/2t,因为s ≥ ηε(Z) ≥ 1。一旦选择,x就以概率ρs(x - c) ≥ exp(-π)输出,这是一个正常数。通过一个标准的重复参数,运行时间是O(t(n))除了指数级的小概率(通过在一定次数的迭代后终止,而不显著地改变输出分布,可以使其为零)。
3.2 Sampling from Arbitrary Lattices




3.3 Sampling with Independent Vectors


4 Trapdoors for Hard Random Lattices
在这一节中,我们将演示某些随机格的trapdoors,非正式地说,它们和最坏情况下的格“一样难”。然后,我们开发一些基础工具和原语,我们的密码应用将建立在其上。
4.1 Random Modular Lattices
(未完待续)