学习时间:2020/07/06 - 2020/07/12
0 主要学习内容
所有我写的代码可以在此处下载:Download
- Basic RNN
- LSTM
1 Basic RNN
RNN神经网络由于具有“记忆”的功能,在自然语言处理(NLP)或者其他序列任务中十分有效。
1.1 RNN Cell
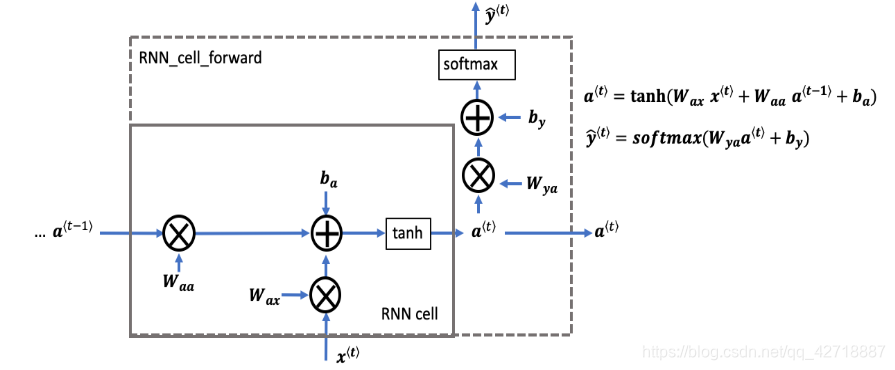
要想了解RNN的工作机制,就需要先从了解RNN的最小组成单元RNN Cell开始。如上图所示,一个RNN Cell的前向传播其实完成了两部分的计算。
a
<
t
>
=
t
a
n
h
(
W
a
x
x
<
t
>
+
W
a
a
a
<
t
−
1
>
+
b
a
)
(1)
a^{<t>} = tanh(W_{ax}x^{<t>} + W_{aa}a^{<t-1>} + b_a) ag 1
a<t>=tanh(Waxx<t>+Waaa<t−1>+ba)(1)
y
^
<
t
>
=
s
o
f
t
m
a
x
(
W
y
a
a
<
t
>
+
b
y
)
(2)
hat{y}^{<t>} = softmax(W_{ya}a^{<t>} + b_y) ag 2
y^<t>=softmax(Wyaa<t>+by)(2)
式子(1)计算的是t时刻隐含的状态,从公式可以看出来
a
<
t
>
a^{<t>}
a<t>由t时刻的输入
x
t
x^{t}
xt和上一层的隐含状态
a
<
t
−
1
>
a^{<t-1>}
a<t−1>这两个量决定的。而这个
a
<
t
>
a^{<t>}
a<t>总是由前一层的隐含状态
a
<
t
−
1
>
a^{<t-1>}
a<t−1>所决定,这就是RNN具有记忆能力的关键。
式子(2)计算的是t时刻的输出
y
^
<
t
>
hat{y}^{<t>}
y^<t>,从公式中可以看出来
y
^
<
t
>
hat{y}^{<t>}
y^<t>由t时刻的隐含状态所决定。
1.2 RNN forward pass
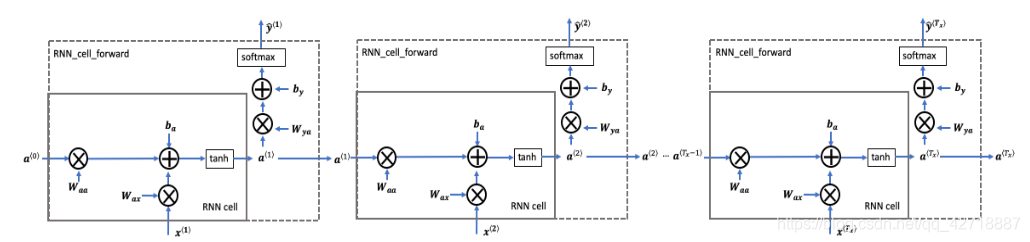
熟悉了上面的cell,这个RNN的前向传播就十分容易理解了。RNN的前向传播就是由多个cell所组成的,将隐含状态一步一步地传递下去就让RNN拥有了记忆功能。
1.3 Basic RNN缺陷分析
从上述的RNN传播过程来看RNN有以下缺陷:
- 隐含状态无法传播太深,从梯度消失(梯度爆炸很容易看出来,这里就不做讨论)的产生原因我们就可以知道,在对参数用链式法则求梯度的过程中也会对 a < t > a^{<t>} a<t>求导,太深的网络就很容易导致梯度消失的现象。
- 从 a < t > a^{<t>} a<t>的计算公式中我们可以看出来,Basic RNN的 a < t > a^{<t>} a<t>记忆力并不强。也就是说,其隐含状态其实在层数太深的时候,难以将很前面的信息传递到较深层。
- 输出 y < t > y^{<t>} y<t>只是与前面的输入有关,而不会考虑到 x < t + 1 > x^{<t+1>} x<t+1>等后面的输入。但是,自然语言处理一般会考虑上下文后再输出结果。
Hints: 上面有关Basic RNN的模型是建立在x输入大小与y输出大小一样的情况下进行的讨论。如果要实现一对多、多对一或者多对多但不一样大的情况,只需要稍微修改一下RNN的结构即可。本次的编程作业考虑的是x与y一样大的情况。
2 LSTM
2.1 LSTM概述
从上述1.3的分析中我们可以看出来Basic RNN层数太深的时候,容易导致梯度消失,并且其记忆长期信息的能力较弱。人们为了解决这两个问题,想出了很多RNN的其他结构。LSTM网络就是其中一种比较常见的网络结构。
2.2 LSTM Cell
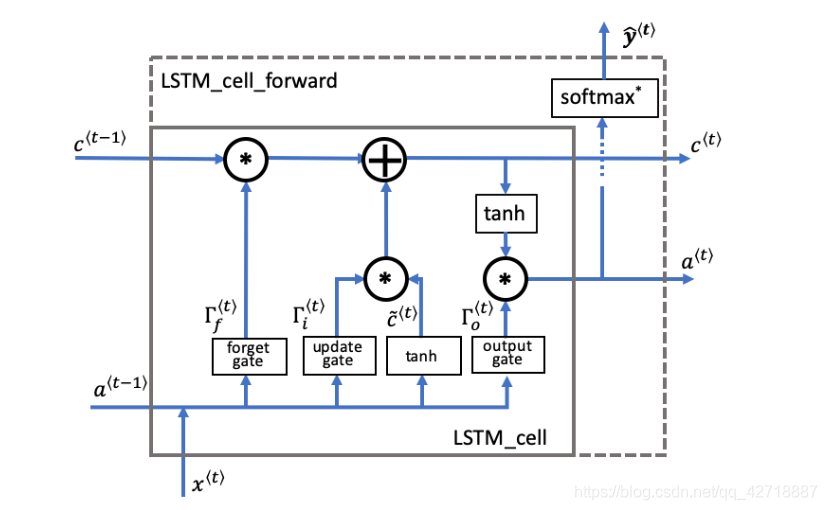
如上图所示,LSTM的最小单元LSTM Cell其实就是在计算这七个量(三个门和四个量):
- Forget gate
Γ
f
<
t
>
Gamma_f^{<t>}
Γf<t>:遗忘门,这个量就是用来控制上一个阶段的细胞状态有多少需要被保留到下一个细胞状态中。
Γ f < t > = σ ( W f [ a < t − 1 > , x < t > ] + b f ) Gamma_f^{<t>} = sigma(W_f [a^{<t-1>}, x^{<t>}] + b_f) Γf<t>=σ(Wf[a<t−1>,x<t>]+bf) - Candidate value
c
~
<
t
>
ilde{c}^{<t>}
c~<t>:候选值,这个量就是用本时刻输入
x
<
t
>
x^{<t>}
x<t>和上一时刻隐含状态
a
<
t
−
1
>
a^{<t-1>}
a<t−1>计算出来的,用来更新本时刻细胞状态的值。
c ~ < t > = t a n h ( W c [ a < t − 1 > , x < t > ] + b c ) ilde{c}^{<t>} = tanh(W_c [a^{<t-1>}, x^{<t>}] + b_c) c~<t>=tanh(Wc[a<t−1>,x<t>]+bc) - Update gate
Γ
i
<
t
>
Gamma_i^{<t>}
Γi<t>:更新门,这个量就是用来控制后选值到底有多少去更新细胞状态。
Γ i < t > = σ ( W i [ a < t − 1 > , x t ] + b i ) Gamma_i^{<t>} = sigma(W_i[a^{<t-1>}, x^{t}] + b_i) Γi<t>=σ(Wi[a<t−1>,xt]+bi) - Cell state
c
<
t
>
c^{<t>}
c<t>:细胞状态,用来记录本时刻细胞的状态。
c < t > = Γ f ∗ c < t − 1 > + Γ i ∗ c ~ < t > c^{<t>} = Gamma_f ast c^{<t-1>} + Gamma_i ast ilde{c}^{<t>} c<t>=Γf∗c<t−1>+Γi∗c~<t> - Output gate
Γ
o
<
t
>
Gamma_o^{<t>}
Γo<t>:输出门,用来控制输出的本时刻隐含状态。
Γ o < t > = σ ( W o [ a < t − 1 > , x t ] + b o ) Gamma_o^{<t>} = sigma(W_o[a^{<t-1>}, x^{t}] + b_o) Γo<t>=σ(Wo[a<t−1>,xt]+bo) - Hidden state
a
<
t
>
a^{<t>}
a<t>:隐含状态,用来计算本时刻的输出和决定下一时刻的各种门的值。
a < t > = Γ o < t > ∗ t a n h ( c < t > ) a^{<t>} = Gamma_o^{<t>} ast tanh(c^{<t>}) a<t>=Γo<t>∗tanh(c<t>) - Prediction
y
^
p
r
e
d
<
t
>
hat{y}^{<t>}_{pred}
y^pred<t>:本时刻的预测输出
y ^ p r e d < t > = s o f t m a x ( W y a < t > + b y ) hat{y}^{<t>}_{pred} = softmax(W_y a^{<t>} + b_y) y^pred<t>=softmax(Wya<t>+by)
2.3 Why LSTM Work?
为什么LSTM能提升记忆能力并且缓解Basic RNN中由于层数过深而导致的梯度消失问题呢?我们可以康康LSTM中所计算的第四个量 c < t > c^{<t>} c<t>(细胞状态),这个量同时由上一个时刻的细胞状态和本时刻的候选值所决定。不像Basic RNN直接把上一个隐含状态直接用来更新本时刻的隐含状态,它采用了两个门(一个遗忘门一个更新门)来决定本时刻细胞状态的更新。我们举个例子来说明,例如:The cat, which ate already, was full. 和 The cats, which ate already, were full. 这两句话,中间的非限制性定语从句相当加了很多个timestap,但是谓语动词的单复数仅仅与很前面cat的单复数有关系,所以我们就需要令更新门接近于0而遗忘门接近于1。这样就保证了细胞状态 c < t > c^{<t>} c<t>在那个非限制性定语从句中基本是以一个常数的形式在传递。这样既能够增强网络的记忆能力,又能够缓解网络在链式求导中产生的梯度消失问题。
2.4 LSTM forward pass
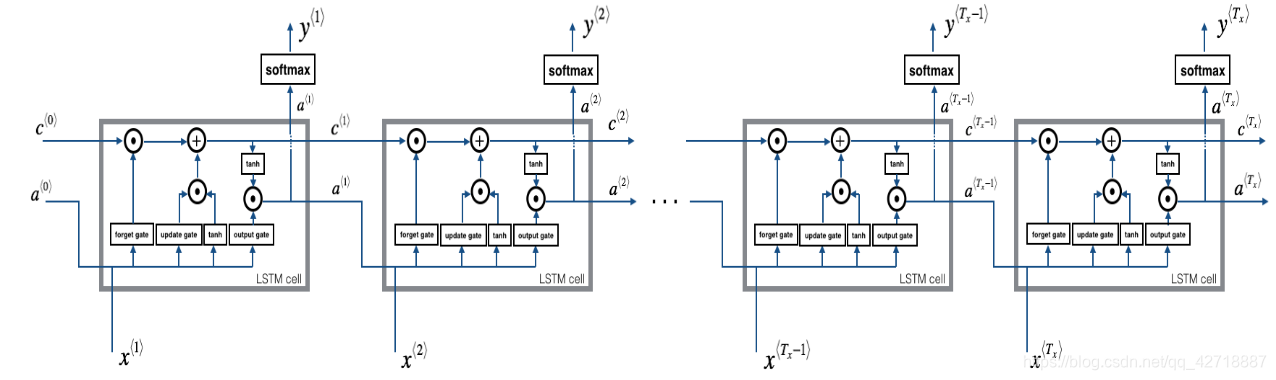
如上图所示,整个LSTM网络的前向传播过程就是把LSTM Cell堆叠起来的过程。