最近在看cs229的视频,为了怕后面忘记,感觉现在先记下来比较好。知识这个东西,长时间不看真的容易忘记。
主要想记一下广义线性模型这块知识。Generalized Linear Models
一、指数族(The exponential family)。
首先先了解一下指数族这个概念:如果一类分布可以写成如下形式,则它可以叫做指数族分布。
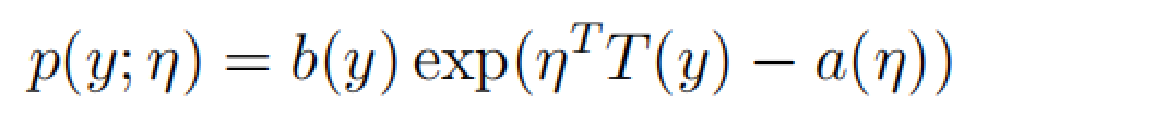
η被称为分布的自然参数(也称为规范参数);
T(y)是充分统计量(对于我们所考虑的分布,通常情况下有T(y)=y);(后面听老师讲解,充分统计量就是说包含样本的所有信息,有了充分统计量就可以把样本扔掉,例如正态分布的期望值和方差,合起来是一个充分统计量,单个的不是)
a(η)被称为对数分割函数;
固定T,a和b,我们可以定义一族以η为参数的分布。也可以这么理解(1)通过改变T,a,b的值,我们可以得到不同的分布,例如Bernoulli分布和Gaussian分布。(2)在固定T,a,b之后,改变η值,就可以得到不同均值的Bernoulli分布和Gaussian分布。
Bernoulli分布和Gaussian分布都是指数族分布的特例,接下来我们将Bernoulli分布和Gaussian分布都转换成指数族分布的形式。
1 Bernoulli分布
Bernoulli(φ) y ∈ {0, 1}, p(y = 1; φ) = φ; p(y = 0; φ) = 1 - φ.
伯努利分布的概率分布函数如下:
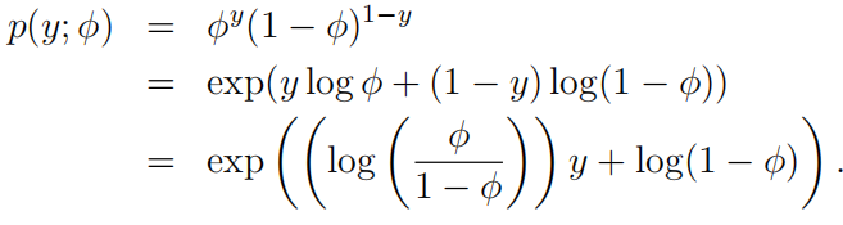
指数族分布:
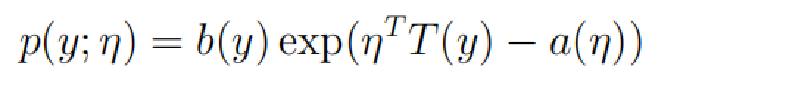
通过以上两个式子进行对比,我们可以得到:
b(y) = 1
T(y) = y
a(η) = - log(1 - φ)
η = log(φ/(1 - φ))
2 Gaussian 分布 (因为 在此处没有影响,所以令 =1)。其实我们可以简单的把高斯分布理解成正态函数。
高斯分布的概率表达函数:
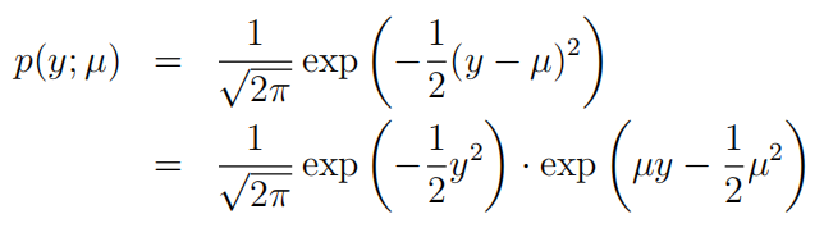
通过对比指数族分布函数,得到
![]()
![]()
![]()
![]()
二、构建广义线性模型Constructing GLMs
首先需要知道三个假设:(可能又要有疑问了,为何要定义这三个假设,他们有什么作用?我们可以把这三个假设理解为我们的设计选择,为了方便后面的过程)
(1) y | x; θ ~ ExponentialFamily(η).
(2)这个地方的E指的是期望的意思![]()
(3) η 和 x是线性相关的![]()
1 Ordinary Least Squares普通最小二乘(属于线性回归)
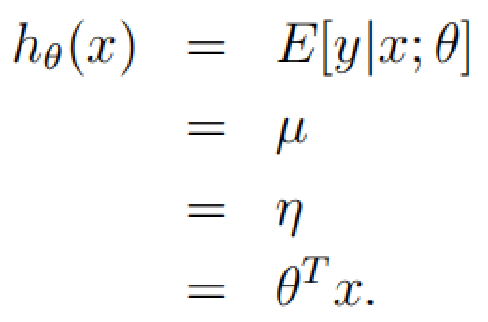
上面四个等式,分别是由assumption 2 ,Gaussian ,assumption 1 ,assumption 3推导出来的
2 Logistic Regression
Bernoulli(φ) y ∈ {0, 1}, p(y = 1; φ) = φ; p(y = 0; φ) = 1 - φ.

上面四个等式分别由assumption ,2 Bernoulli ,η = log(φ/(1 - φ))(前面得到), assumption 3推导出来的
3 Softmax Regression
比较难的就是这个多分类的情况,在多分类情况下,y ∈ {1 2, . . . , k}.要在k个可能的结果上参数化多项式,可以使用k个参数φ1,,φk指定每个结果的概率。同时我们需要知道所有概率之和为1.
![]()
并且
![]()
指示器函数如该等式所示,中括号里面若是真命题,该值就等于1,否就等于0![]()
此时的T(y)和前面不同,前面T(y)=y,这里T(y)是一个k-1维的向量,而不是一个实数,定义T(y)如下形式:(为什么要定义成这个样子,我们可以简单理解为这样定义是为了后面更好的构建广义线性模型)
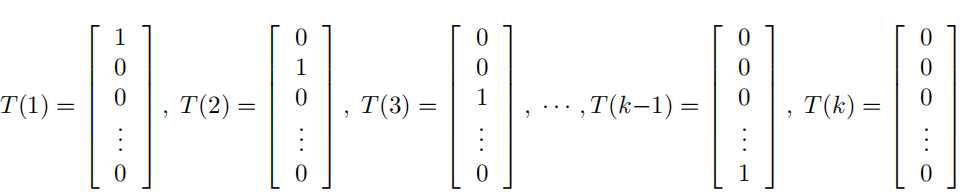
接下来我们就可以得出![]() ,等式左边代表T(y)的第i个元素,然后进一步得到
,等式左边代表T(y)的第i个元素,然后进一步得到![]()
概率分布函数
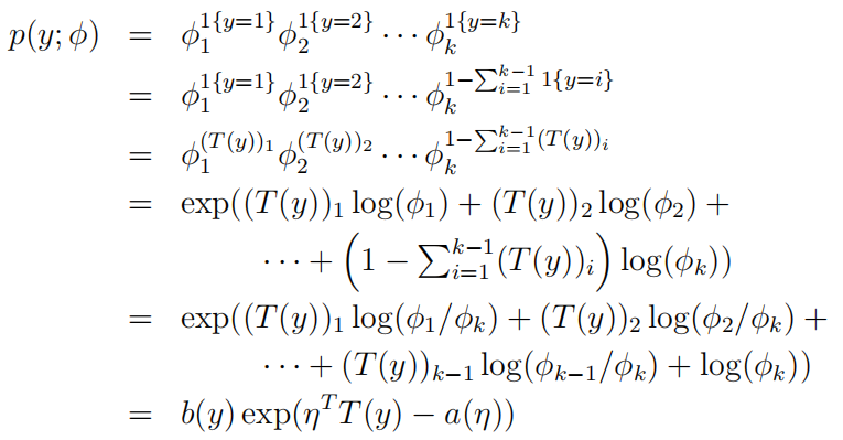
为了更加直观,我将第五个等式转换成如下图形式:

然后可以推出:
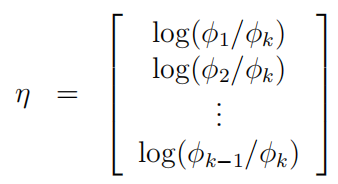
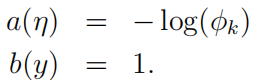
之后:
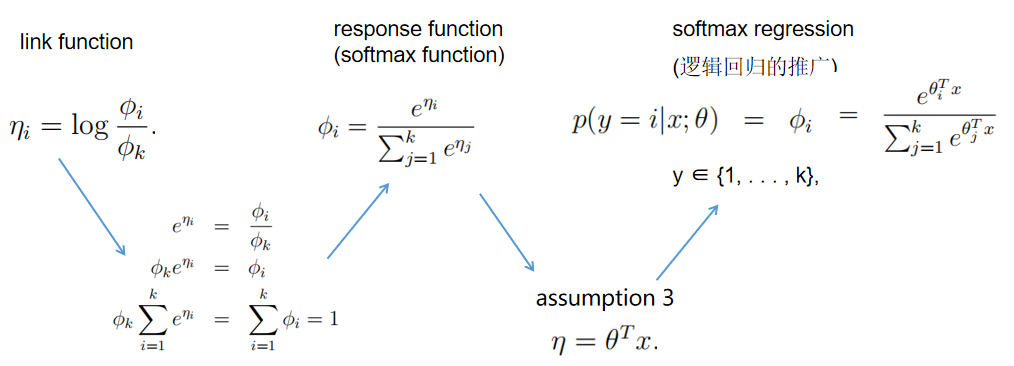
学习算法输出p(y = i|x; θ),i = 1, . . . , k

最后是对数似然函数:
假设有m个训练样本![]()
利用最大似然法去学习模型参数θ
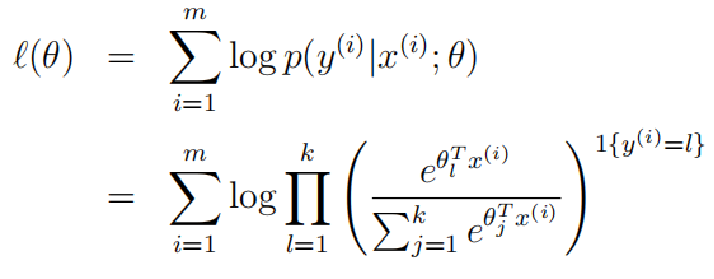
这一部分大致就完了,后面写的不太能理解,因为我自己理解的也不是很透彻。这些公式是可以一步步推出来的,但是由于自己理解有限,写的不是很明白。再接再厉,加油!