题解 luogu P1251 【餐巾计划问题】

题解 luogu P1251 【餐巾计划问题】

时间：2019.3.19

网络流24题：【餐巾计划问题】

题目描述

一个餐厅在相继的 \(N\) 天里,每天需用的餐巾数不尽相同。假设第 \(i\) 天需要 \(r_i\) 块餐巾(\(i=1,2,...,N\))。餐厅可以购买新的餐巾,每块餐巾的费用为 \(p\) 分;或者把旧餐巾送到快洗部,洗一块需 \(a\) 天,其费用为 \(f\) 分;或者送到慢洗部,洗一块需 \(b\) 天(\(b>a\)),其费用为 \(s\) 分(\(s < f\))。

每天结束时,餐厅必须决定将多少块脏的餐巾送到快洗部,多少块餐巾送到慢洗部,以及多少块保存起来延期送洗。但是每天洗好的餐巾和购买的新餐巾数之和,要满足当天的需求量。

试设计一个算法为餐厅合理地安排好 \(N\) 天中餐巾使用计划,使总的花费最小。编程找出一个最佳餐巾使用计划。

建图（1）

考虑建出下面这张图：

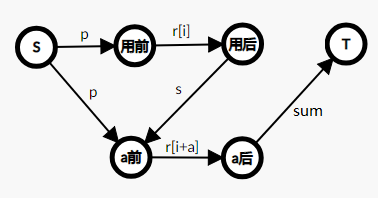
将每天当成一个点，根据当天的餐巾是否已使用，拆成前和后。
\(S\)向前连边，费用为\(p\)，表示可以任意买新餐巾
前向后连边，容量为\(r_i\)，表示需要使用\(r_i\)条餐巾。
第\(N\)个后向\(T\)连边，容量为\(\sum r_i\)，表示需要将所有餐巾用掉。
每天后向\(a\)天后的前连边，费用为\(s\)，表示送到快洗部（慢洗部同理）

---

这样，我们只需要控制流向后的流量均为\(r_i\)就行了。

但是，这样就出现一个问题：我们没办法控制流向后的流量刚好流满呀？

看来我们要改变建图方式了。

建图（2）

建出下面这张图：

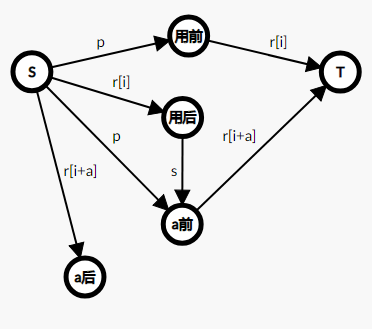
将每天当成一个点，根据当天的餐巾是否已使用，拆成前和后。
\(S\)向前连边，费用为\(p\)，表示可以任意买新餐巾。
前向\(T\)连边，容量为\(r_i\)，表示要消耗\(\textbf{r}_\textbf{i}\)条餐巾。
\(S\)向后连边，容量为\(r_i\)，表示收到用前产生的\(\textbf{r}_\textbf{i}\)条旧餐巾。
每天后向\(a\)天后的前连边，费用为\(s\)，表示送到快洗部（慢洗部同理）

---

这样建图意味着前的流与后的流意义不同。
从\(S\)（或几天前的后）流向前的流表示能使用的新餐巾，
而从\(S\)流向后的流表示使用后留下的\(r_i\)条旧餐巾。

我们控制了从前流出的餐巾（即使用数量）为\(r_i\)，而流进后的餐巾数量刚好为\(r_i\)

代码

注意上面没有讲到的一点：使用前多余的干净餐巾可以留到明天再使用。
将今天的前向明天的前连边即可。

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int kMaxN = 2000 * 2 + 10;
const int kMaxM = kMaxN * 4;
const int kInf = 4e18;
struct Graph {
  struct Arc {
    int to, cap, cost;
    int next;
  };
  Arc arcs[kMaxM << 1];
  int top, head[kMaxN];
  Graph() { top = 1; }
  void Add(int u, int v, int cap, int cost) {
    arcs[++top] = (Arc) {v, cap, cost, head[u]};
    head[u] = top;
    arcs[++top] = (Arc) {u, 0, -cost, head[v]};
    head[v] = top;
  }
  int s, t;
  queue<int> Q;
  bool in[kMaxN];
  int cost[kMaxN], flow[kMaxN], last[kMaxN];
  bool Spfa() {
    memset(flow, 0, sizeof(flow));
    memset(last, 0, sizeof(last));
    memset(cost, 0x7F, sizeof(cost));
    // 不用memset flow和last
    // 这两个数组不参与最短路计算
    // 一定要写flow[t] = 0
    // 如果有负环一定要写memset(in)
    Q.push(s);
    cost[s] = 0;
    flow[s] = kInf;
    flow[t] = 0; // !!!
    while (!Q.empty()) {
      int u = Q.front();
      Q.pop();
      in[u] = false;
      for (int i = head[u]; i; i = arcs[i].next) {
        Arc& arc = arcs[i];
        int v = arc.to;
        if (cost[u] + arc.cost < cost[v] && arc.cap) {
          cost[v] = cost[u] + arc.cost;
          flow[v] = min(flow[u], arc.cap);
          last[v] = i;
          if (!in[v]) {
            in[v] = true;
            Q.push(v);
          }
        }
      }
    }
    return flow[t] != 0;
  }
  int max_flow, min_cost;
  void Update() {
    int u = t;
    while (u != s) {
      int i = last[u];
      arcs[i].cap -= flow[t];
      arcs[i ^ 1].cap += flow[t];
      u = arcs[i ^ 1].to;
    }
    max_flow += flow[t];
    min_cost += cost[t] * flow[t];
  }
  void Ek() {
    max_flow = min_cost = 0;
    while (Spfa()) Update();
  }
};
Graph G;
int n;
int p, a, f, b, s;
#define UNUSED(I) (I)
#define USED(I) ((I) + 2001)
signed main() {
  scanf("%lld", &n);
  G.s = kMaxN - 2;
  G.t = kMaxN - 1;
  for (int i = 1; i <= n; i++) {
    int r;
    scanf("%lld", &r);
    G.Add(UNUSED(i), G.t, r, 0);
    G.Add(G.s, USED(i), r, 0);
  }
  scanf("%lld %lld %lld %lld %lld",
        &p, &a, &f, &b, &s);
  for (int i = 1; i <= n; i++) {
    G.Add(G.s, UNUSED(i), kInf, p);
    if (i + 1 <= n) G.Add(UNUSED(i), UNUSED(i + 1), kInf, 0);
    if (i + a <= n) G.Add(USED(i), UNUSED(i + a), kInf, f);
    if (i + b <= n) G.Add(USED(i), UNUSED(i + b), kInf, s);
  }
  G.Ek();
  // printf("%lld %lld\n", G.min_cost, G.max_flow);
  printf("%lld\n", G.min_cost);
  return 0;
}