感知器python

感知器学习的目标是求得一个能够将训练集正实例点和负实例点·完全正确分开的分离超平面。即找到这超平面的参数w,b。

超平面定义

w*x+b=0

其中w是参数，x是数据。公式很好理解以二维平面为例，w有两个参数x0,x1。确定其中一个参数x0就可以确定另一个参数x1所以，二维中超平面w*x+b=0就是一条直线。三维中，w有三个参数w0,w1,w2。确定其中两个就可以确定另一个参数，所以超平面是一个面。

找到超平面后，超平面上面的是的是正类，下面的是负类，可以将线性可分数据集分开。其中定义中的w是超平面的法向量，因为对于二维平面，w*x1-b=0,w*x2-b=0。联立得w*(x1-x2)=0，而x1,x2是线段上的点，因此x1-x2表示此线段的一个向量，w与(x1,x2)做点积等于0，因此w垂直与此向量，即w垂直于超平面。

知道w垂直与超平面即可以推出空间上的一个点x0到超平面的距离公式为|w*x0+b|÷||w||。推导在这里

请问d=|Ax0+By0+C|/√(A²+B²)是什么公式?从哪里推出的? - silvergin的回答 - 知乎 https://www.zhihu.com/question/56356774/answer/148814257

对于误分类的点（xi,yi）来说,-yi(w*xi+b)>0，因为如果分类错误，那么预测的y与真实标签值符号相反，所以相乘等于-1，加个负号等于+1，大于0.（假设正类标签为1，负类标签为-1）

因此将所有的误分类点加起来得到损失函数。，不考虑可，以得到即为损失函数，我们只要优化这个函数，就能求得超平面的参数w,跟b

优化方法极为梯度下降法，梯度公式为：对w求偏导为,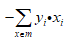,对b求偏导为。

下面给出代码：

import numpy as np
from matplotlib import pyplot as plt
def data(num):
    '''
    生成线性可分数据集，分界线为x0-x1+100=0
    :param num:
    :return:
    '''
    X = np.random.randint(0,101,(2,num))
    y = np.zeros(num)
    y[X[0,:]>=(100-X[1,:])] = 1
    y[X[0,:]<(100-X[1,:])] = -1
    return X,y
def plot_data(X,y,w,b):
    '''
    绘制散点图
    :param X:
    :param y:
    :param w:
    :param b:
    :return:
    '''
    plt.scatter(X[0,y==1],X[1,y==1],s=15,c='b',marker='o')
    plt.scatter(X[0,y==-1],X[1,y==-1],s=15,c='g',marker='x')
    plt.plot([0,-b/w[0]],[-b/w[1],0],c='r')
    plt.show()
def mistake(X,y,w,b):
    '''
    找到错误分类
    :param X:
    :param y:
    :param w:
    :param b:
    :return:
    '''
    return y*(w.dot(X)+b)<0
def compute_cost(X,y,w,b,c):
    '''
    计算损失值
    :param X:
    :param y:
    :param w:
    :param b:
    :param c:
    :return:
    '''
    return -np.sum(y[c]*(w.dot(X[:,c])+b))
def grad(X,y,c):
    '''
    计算梯度
    :param X:
    :param y:
    :param c:
    :return:
    '''
    dw = -np.sum(y[c]*X[:,c]，axis=1)
    db = -np.sum(y[c])
    return dw,db
def updata_parameters(w,b,dw,db,learning_rate):
    '''
    梯度下降，更新参数
    :param w:
    :param b:
    :param dw:
    :param db:
    :param learning_rate:
    :return:
    '''
    w = w-learning_rate*dw
    b = b-learning_rate*db*100
    return w,b
#生成线性可分数据集，初始化参数
X,y = data(50)
w = np.random.rand(2)
b = 0
#计算错误分类点，求损失值
c = mistake(X,y,w,b)
cost = compute_cost(X,y,w,b,c)
i = 0
#当有错位分类点不停迭代
while cost>0:
    # if i%500==0:
    #     print('迭代{0}次，损失值为{1}:'.format(i,cost))
    dw,db = grad(X,y,c)#计算梯度
    w,b = updata_parameters(w,b,dw,db,0.001)#更新参数
    c = mistake(X,y,w,b)#求错误分类点，bool数组形式
    cost = compute_cost(X,y,w,b,c)#计算损失值
    i = i+1
#绘制图像，打印参数
plot_data(X,y,w,b)
print(w,b)

输出为：

最好设定迭代次数，因为学习速率与生成的数据集的原因可能会迭代很差时间才会求出结果。学习速率过大，导致在正确结果附近跌宕。学习速率过小导致学习速度缓慢。

书上还提到了，感知器算法的对偶形式，对偶形式的讲解在这里

如何理解感知机学习算法的对偶形式？ - 知乎 https://www.zhihu.com/question/26526858

参考：李航，统计学习方法