Jaccard similarity coefficient(杰卡德相似系数):
两个集合A和B的交集元素在A,B的并集中所占的比例,称为两个集合的杰卡德相似系数
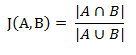
Correlation coefficient(相关系数):
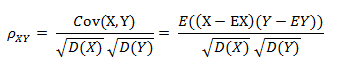
准确率、召回、Fscore:
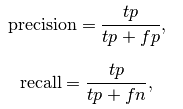
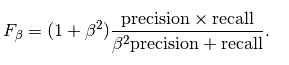
Hinge Loss:
$L(y(wx + b)) = [1 - y(wx + b)]_+$
Log Loss:
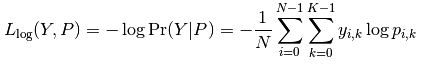
$ Loss(y, f(x)) = log(1 + exp(-yf(x))) $
Receiver operating characteristic (ROC) && AUC:
对于分类器,评价指标主要有precision,recall,F-score,以及auc.样本在不同类别上的不均衡分布,导致accuracy这样的度量标准不能恰当的反映分类器的表现。当测试集中的正负样本的分布变化的时候,ROC曲线能够保持不变。
针对一个二分类问题,将实例分成正类(postive)或者负类(negative)。但是实际中分类时,会出现四种情况:
(1)若一个实例是正类并且被预测为正类,即为真正类(True Postive TP)
(2)若一个实例是正类,但是被预测成为负类,即为假负类(False Negative FN)
(3)若一个实例是负类,但是被预测成为正类,即为假正类(False Postive FP)
(4)若一个实例是负类,但是被预测成为负类,即为真负类(True Negative TN)
roc曲线:
横轴:false postive rate FPR = FP/(FP+TN) 负类中预测错误的比例 FPR越大,预测正类中实际负类越多
纵轴:true postive rate TPR = TP/(TP+FN) 正类中预测正确的比例 TPR越大,预测正类中实际正类越多 FPR与TPR没有相关性,TPR越大越好,FPR越小越好
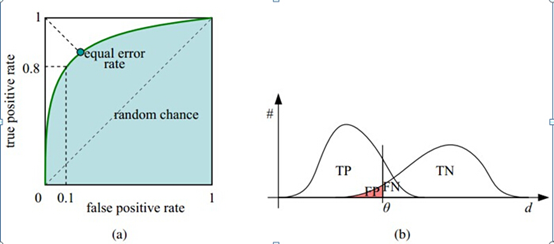
理想目标:TPR=1,FPR=0,即图中(0,1)点,故ROC曲线越靠拢(0,1)点,越偏离45度对角线越好 (1,1):全部预测为正类 (0,0):全部预测为负类
AUC(Area under Curve):Roc曲线下的面积,介于0.5和1之间。Auc作为数值可以直观的评价分类器的好坏,值越大越好
对于一个特定的分类器和测试数据集,显然只能得到一个分类结果,即一组FPR和TPR结果,而要得到一个曲线,我们实际上需要一系列FPR和TPR的值。由分类算法算出每个测试样本属于正样本的概率(score), 从高到低,依次将“Score”值作为阈值threshold,当测试样本属于正样本的概率大于或等于这个threshold时,我们认为它为正样本,否则为负样本.每次选取一个不同的threshold,我们就可以得到一组FPR和TPR,即ROC曲线上的一点,这样即可画出ROC曲线。
AUC计算:
1、一个关于AUC的很有趣的性质是,它和Wilcoxon-Mann-Witney Test是等价的。而Wilcoxon-Mann-Witney Test就是测试任意给一个正类样本和一个负类样本,正类样本的score有多大的概率大于负类样本的score(score理解为预测属于正样本的概率)。有了这个定义,我们就得到了另外一种计 算AUC的办法:得到这个概率。我们知道,在有限样本中我们常用的得到概率的办法就是通过频率来估计之。这种估计随着样本规模的扩大而逐渐逼近真实值。这 和上面的方法中,样本数越多,计算的AUC越准确类似,也和计算积分的时候,小区间划分的越细,计算的越准确是同样的道理。具体来说就是统计所有的 M×N(M为正类样本的数目,N为负类样本的数目)个正负样本对中,有多少个组中的正样本的score大于负样本的score。当二元组中正负样本的 score相等的时候,按照0.5计算。然后除以MN。实现这个方法的复杂度为O(n^2)。n为样本数(即n=M+N)
2、 首先对score从大到小排序,然后令最大score对应的sample 的rank为n,第二大score对应sample的rank为n-1,以此类推。然后把所有的正类样本的rank相加,再减去两个正样本组合的情况(此处我觉得是m(m-1)/2)。得到的就是所有的样本中有多少对正类样本的score大于负类样本的score。然后再除以M×N。即
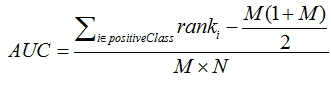
从AUC判断分类器(预测模型)优劣的标准:
- AUC = 1,是完美分类器,采用这个预测模型时,不管设定什么阈值都能得出完美预测。绝大多数预测的场合,不存在完美分类器。
- 0.5 < AUC < 1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
- AUC = 0.5,跟随机猜测一样(例:丢铜板),模型没有预测价值。
- AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测,因此不存在AUC < 0.5的情况。
Mean absolute error:
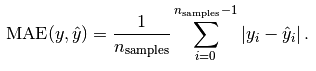
Mean squared error:
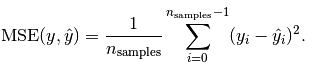
http://scikit-learn.org/stable/modules/model_evaluation.html#scoring-parameter