过拟合的原因:使用的模型过于复杂,根据VC维理论:VC维很高的时候,就容易发生bias很低,但variance很高的情形.
解决过拟合最常用的方法就是regularization, 常用的有:L1正则, L2正则等.L1正则会使得参数稀疏化, L2正则可以起到平滑的作用, 从贝叶斯理论的角度审视下正则化.
从贝叶斯的角度来看, 正则化等价于对模型参数引入先验分布.(先验概率可理解为统计概率,后验概率可理解为条件概率)
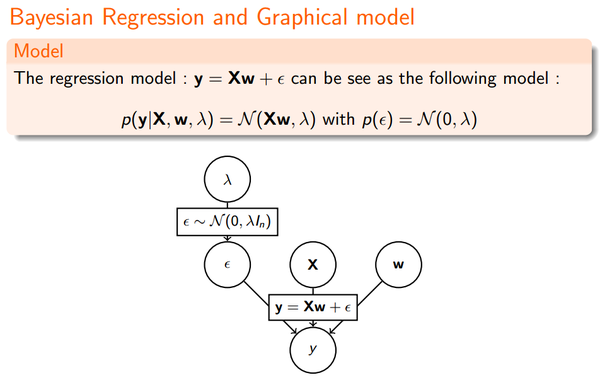
一. Linear Regression
我们先看下最原始的Linear Regression:
此处以 http://www.cnblogs.com/ljygoodgoodstudydaydayup/p/6738597.html 为准
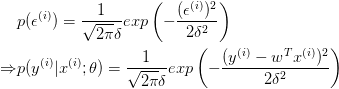
由最大似然估计,
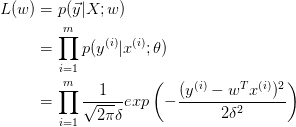
取对数:
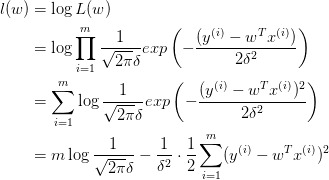
即:
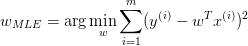
这就导出了我们原始的 least-squares 损失函数,但这是在我们对参数 w 没有加入任何先验分布的情况下。在数据维度很高的情况下,我们的模型参数很多,模型复杂度高,容易发生过拟合。这个时候,我们可以对参数 w 引入先验分布,降低模型复杂度。
Ridge Regression
我们对参数w引入协方差为a的零均值高斯先验.(每一个分量都服从该分布)
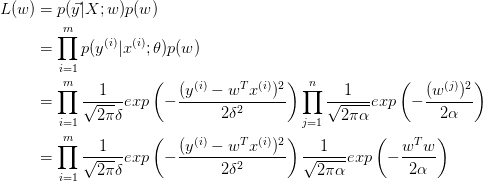 左式有点问题,参数w的高斯先验项的系数少了个连乘符号
左式有点问题,参数w的高斯先验项的系数少了个连乘符号
取对数:
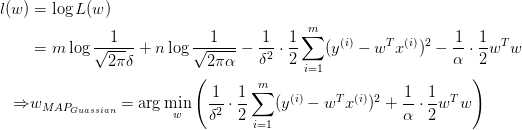
等价于:
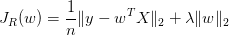
上式即Ridge Regression.对参数引入高斯先验等价于L2正则化
ridge regression 并不具有产生稀疏解的能力,也就是说参数并不会真出现很多零。假设我们的预测结果与两个特征相关,L2正则倾向于综合两者的影响,给影响大的特征赋予高的权重;而L1正则倾向于选择影响较大的参数,而舍弃掉影响较小的那个。实际应用中 L2正则表现往往会优于 L1正则,但 L1正则会大大降低我们的计算量。
拉普拉斯分布:
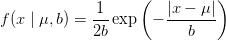
重复之前的推导过程我们很容易得到:
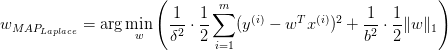
总结:
正则化参数等价于对参数引入先验分布,使得 模型复杂度 变小(缩小解空间),对于噪声以及 outliers 的鲁棒性增强(泛化能力)。整个最优化问题从贝叶斯观点来看是一种贝叶斯最大后验估计,其中 正则化项 对应后验估计中的 先验信息,损失函数对应后验估计中的似然函数,两者的乘积即对应贝叶斯最大后验估计的形式。
转自:
https://www.zhihu.com/question/23536142