网络流学习笔记
- 简介网络流
网络流应该是NOIP考纲范围内一个比较难的知识点,其实用心学习还是觉得比较简单。
这里用最通俗的语言讲一讲我认识中的网络流,显然是一个初步的概念。
解决网络流问题总是变成这样一个模型:
想象你现在面前有一个城市的排水系统,是由一个个单向联通的管道组成的,其中有一个节点S可以源源不断的流出水,另一个节点T可以源源不断的吸收水,
除此之外其他节点只能流入和流出水,不能排入或者排出水,而管道的粗细是一定的,每根管道在同一时间只能流入一个上限的流量c,现在让你对这个网络进行分析。
1. 求这个网络的S节点(源点)可以在同一时刻流出水的最大流量
2. 若每个管道有一个输送费用(单位流量的花费),求第1问的若干方案里面,保证最大流量基础上,最小代价是多少
3. 若每个管道有一个输送价值(单位流量的价值),求第1问的若干方案里面,保证最大流量基础上,最大价值是多少
这里我们会用最通熟易懂的语言讲述这三个常规问题的做法。
- 流量网络的分析(最简单的概念)
引入一个概念流量网络,什么是流量网络,就是给你的原始的流量图只有每条边的限流而具体的最大可行的流量未知
引入一个概念可行流量,我们定义一个函数f(u,v)这个由一个二元组映射到一个值表示一条边(u,v)∈E 的可行流量。
引入一个概念限流量,c(u,v)表示一条边(u,v)∈E,由于一些限制最多能流经的流量(最大值)
人为定义,一条反边的限流量是0
显然由于我们对每条边的限制就有一个重要的定理
定理1(容量限制):f(u,v)≤c(u,v)
对于上面这个实例的分析我们应该能够得出一些信息,
由定义可知,对于源点T可以源源不断流出,对于汇点T,可以源源不断的吸收。
而对于非源点非汇点的一般点,流入总量等于流出总量。
定理2(流量守恒性): 任取u≠S,u≠T,必有∑f(x,u)=∑f(u,y) (x,u),(u,v)∈E
即对于一般点,总流入等于总流出
我们人为规定当一个网络有从u流向v的一个正流量D的时候,那么从v流向u一定存在一个-D的流量(是负数)与之对应,
由于这个定义,我们得出一个对称的性质:
定理3(斜对称性): f(u,v)=-f(v,u)
引入一个概念残量网络,对于一条边的可行流和限流量之间还有提升的空间,我们考虑弥补这一空间,这样的差值就是一条边的残量,对于每一条边的残量组成的网络就是残量网络,
可以这么写f‘(u,v)=c(u,v)-f(u,v),残量网络指的是F={f(u,v)|(u,v)∈E}
- 最大流模型和算法(EK算法和Dinic算法)
想象你现在面前有一个城市的排水系统,是由一个个单向联通的管道组成的,其中有一个节点S可以源源不断的流出水,另一个节点T可以源源不断的吸收水,
除此之外其他节点只能流入和流出水,不能排入或者排出水,而管道的粗细是一定的,每根管道在同一时间只能流入一个上限的流量c,现在让你对这个网络进行分析。
1. 求这个网络的S节点(源点)可以在同一时刻流出水的最大流量
- EK算法
考虑公式:f'(u,v)=c(u,v)-f(u,v)
要解决上面这个问题,首先我们建出一个残量网络:
对于每条单向的管道(u,v,w),连一条u到v的残量是w的一条边,一条(v,u)残量是0的一条边。
考虑在残量网络中是不是存在从S到T的一条合法路径使其经过路径上的流量残量都是正数,然后在这条路径上的残量最小值就是可以增加的那么一点点流量Min。
我们考虑在,这条路径上每一条反边的残量加上一个Min,正边的残量减去一个Min,(每次走的时候不走反边!)就完成的一次更新,显然可用BFS实现,
当残量网络中无S到T都大于0的路径时说明已经找到最大流!
这就是EK算法。
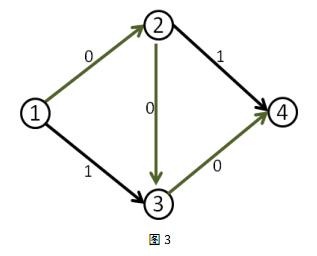
在找到1-2-3-4这条增广路之后,把容量修改成如下

时再找增广路的时候,就会找到1-3-2-4这条可增广量,即delta值为1的可增广路。将这条路增广之后,得到了最大流2。
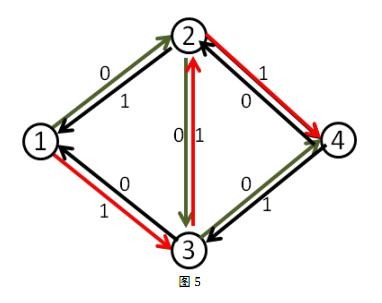
那么,这么做为什么会是对的呢?我来通俗的解释一下吧。
事实上,当我们第二次的增广路走3-2这条反向边的时候,就相当于把2-3这条正向边已经是用了的流量给”退”了回去,不走2-3这条路,而改走从2点出发的其他的路也就是2-4。(有人问如果这里没有2-4怎么办,这时假如没有2-4这条路的话,最终这条增广路也不会存在,因为他根本不能走到汇点)同时本来在3-4上的流量由1-3-4这条路来”接管”。而最终2-3这条路正向流量1,反向流量1,等于没有流量。
这就是这个算法的精华部分,利用反向边,使程序有了一个后悔和改正的机会
EK算法最坏时间复杂度是O(nm2)但是在实际使用中可以处理1e3到1e4的网络
# include<bits/stdc++.h> using namespace std; const int INF=0x7f7f7f7f7f,N=1e4+10,M=1e5+10; struct A{ int pre,to,w; }a[M*2]; int head[N],pre[N],incf[M*2]; int n,m,S,T,tot=1,maxflow; bool vis[N]; void adde(int u,int v,int w) { a[++tot].pre=head[u]; a[tot].to=v; a[tot].w=w; head[u]=tot; a[++tot].pre=head[v]; a[tot].to=u; a[tot].w=0; head[v]=tot; } bool find() { memset(pre,-1,sizeof(pre)); memset(vis,false,sizeof(vis)); queue<int>q; q.push(S); vis[S]=true; incf[S]=INF; while (!q.empty()) { int u=q.front(); q.pop(); for (int i=head[u];i;i=a[i].pre) { int v=a[i].to; if (vis[v]||a[i].w<=0) continue; incf[v]=min(incf[u],a[i].w); pre[v]=i; q.push(v),vis[v]=true; if (v==T) return true; } } return false; } void update() { int x=T; while (x!=S) { int i=pre[x]; a[i].w-=incf[T]; a[i^1].w+=incf[T]; x=a[i^1].to; } maxflow+=incf[T]; } int main() { scanf("%d%d%d%d",&n,&m,&S,&T); int u,v,w; for (int i=1;i<=m;i++) { scanf("%d%d%d",&u,&v,&w); adde(u,v,w); } maxflow=0; while (find()) update(); printf("%d ",maxflow); return 0; }
- Dinic算法
考虑这样一个问题,EK算法的增广路只能一条一条找能不能有一种更快的找法呢,一下找多条,一次bfs找多条增广路。
于是Dinic就应运而生了!!
我们定义每个点的层次dep表示从S到这个点最少要经过几个点,蓝色的就是每个点的dep值,显然可以用BFS做

这样子我们就完成了图的分层。dep值一样的就是同一层。
有了每个点的层数编号,对任意点u到点d的路径如果有dep[d]==dep[u]+1,我们就可以判断该路径在一条最短增广路上。
为什么要找最短增广路?
举个极端例子:
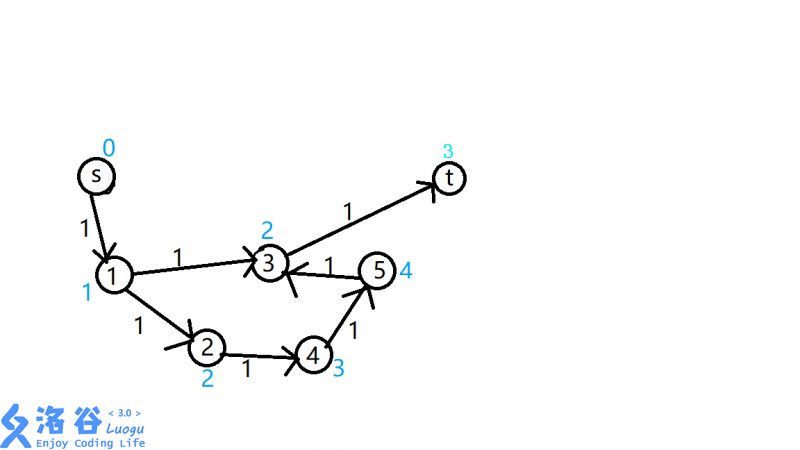
有了分层,我们就不会选S->1->2->4->5->3->T 了
在Dinic中,我们找增广路是用深搜:
再放一次刚才的图:
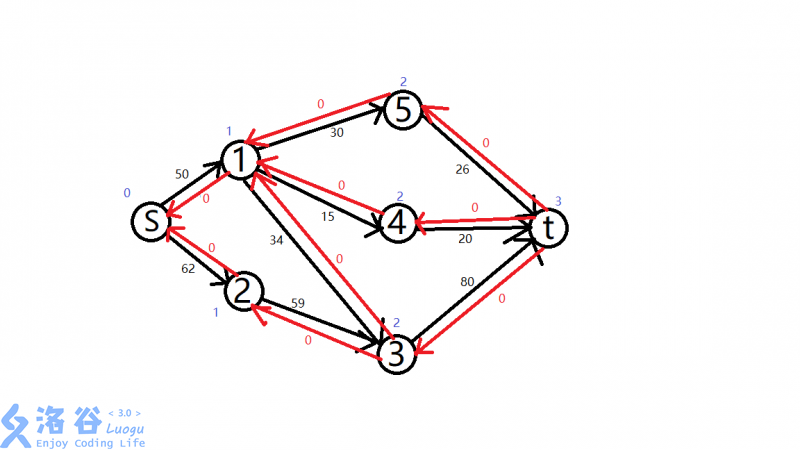
分完了层就要开始找增广路了。
比如说,第一次我们找S->1->4->T:

路径已经标出来了,再仔细看一看图,发现了什么?
还有增广路,标号还可以继续利用!!!那我们可以再执行一次dfs
继续利用第一次bfs出来的标号,再找第二条增广路:
S->1->5->T:
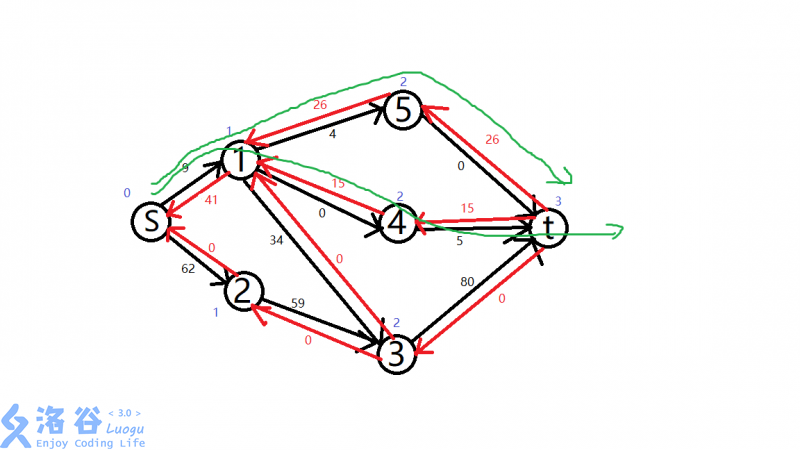
再找找 竟然还能继续利用标号找第三条增广,再执行dfs
S->1->3->T:

还有第四条!再执行dfs
S->2->3->T:
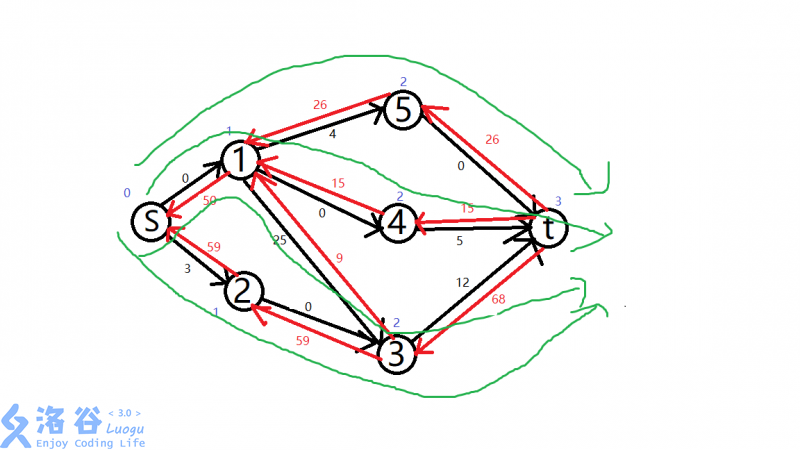
发现了吗?一次bfs我们找了4条增广路!
于是这样的算法最坏时间复杂度是O(nm2),可以处理1e4-1e5的流量网络!
# include <bits/stdc++.h> using namespace std; const int N=1e4+10,M=1e5+10; struct rec{ int pre,to,f;}a[M*2]; int head[N],dep[N]; int n,m,S,T,tot=1; bool inq[N]; void adde(int u,int v,int f) { a[++tot].pre=head[u];a[tot].to=v; a[tot].f=f; head[u]=tot; a[++tot].pre=head[v];a[tot].to=u; a[tot].f=0; head[v]=tot; } bool bfs() { queue<int>q; memset(dep,0x3f,sizeof(dep)); memset(inq,false,sizeof(inq)); q.push(S); inq[S]=true; dep[S]=0; while (!q.empty()) { int u=q.front();q.pop(); inq[u]=false; for (int i=head[u];i;i=a[i].pre) { int v=a[i].to; if (dep[v]>dep[u]+1&&a[i].f) { dep[v]=dep[u]+1; if (!inq[v]) q.push(v),inq[v]=true; } } } return dep[T]!=0x3f3f3f3f; } int dfs(int u,int flow) { if (u==T) return flow; for (int i=head[u];i;i=a[i].pre) { int v=a[i].to,f=a[i].f; if (f==0||dep[v]!=dep[u]+1) continue; int tmp=dfs(v,min(flow,f)); if (tmp) { a[i].f-=tmp; a[i^1].f+=tmp; return tmp;} } return 0; } int main() { scanf("%d%d%d%d",&n,&m,&S,&T); int u,v,f; for (int i=1;i<=m;i++) { scanf("%d%d%d",&u,&v,&f); adde(u,v,f); } int flow=0,tmp; while (bfs()) { while (tmp=dfs(S,0x3f3f3f3f)) flow+=tmp; } printf("%d ",flow); return 0; }
- 费用流模型和算法(EK算法)
想象你现在面前有一个城市的排水系统,是由一个个单向联通的管道组成的,其中有一个节点S可以源源不断的流出水,另一个节点T可以源源不断的吸收水,
除此之外其他节点只能流入和流出水,不能排入或者排出水,而管道的粗细是一定的,每根管道在同一时间只能流入一个上限的流量c,现在让你对这个网络进行分析。
2. 若每个管道有一个输送费用(单位流量的花费),求第1问的若干方案里面,保证最大流量基础上,最小代价是多少
3. 若每个管道有一个输送价值(单位流量的价值),求第1问的若干方案里面,保证最大流量基础上,最大价值是多少
对于我们的EK算法我们是任意找到一条增广路我们就增广了,然而没有考虑最小费用这个条件,
我们不妨每次增广花费最小的一条增广路,一直增广到无法增广为止,求出的最大流就是最小费用最大流!
把BFS改成SPFA(或者Dijkstra【负权边你就暴力加上一个大数】)就行了。。
# include<bits/stdc++.h> using namespace std; const int INF=0x7f7f7f7f7f,N=1e4+10,M=1e5+10; struct A{ int pre,to,f,w; }a[M*2]; int head[N],pre[N],incf[M*2],d[N]; int n,m,S,T,tot=1,maxflow,mincost; bool inq[N]; void adde(int u,int v,int f,int w) { a[++tot].pre=head[u]; a[tot].to=v; a[tot].f=f; a[tot].w=w; head[u]=tot; a[++tot].pre=head[v]; a[tot].to=u; a[tot].f=0; a[tot].w=-w; head[v]=tot; } bool SPFA() { queue<int>q; memset(d,0x3f,sizeof(d)); memset(inq,false,sizeof(inq)); q.push(S); d[S]=0; inq[S]=true; incf[S]=INF; while (!q.empty()) { int u=q.front(); inq[u]=false; q.pop(); for (int i=head[u];i;i=a[i].pre) { if (a[i].f<=0) continue; int v=a[i].to,w=a[i].w,f=a[i].f; if (d[v]-w>d[u]) { d[v]=d[u]+w; incf[v]=min(incf[u],f); pre[v]=i; if (!inq[v]) inq[v]=true,q.push(v); } } } return d[T]!=0x3f3f3f3f; } void update() { int x=T; while (x!=S) { int i=pre[x]; a[i].f-=incf[T]; a[i^1].f+=incf[T]; x=a[i^1].to; } maxflow+=incf[T]; mincost+=d[T]*incf[T]; } int main() { scanf("%d%d%d%d",&n,&m,&S,&T); int u,v,f,w; for (int i=1;i<=m;i++) { scanf("%d%d%d%d",&u,&v,&f,&w); adde(u,v,f,w); } maxflow=mincost=0; while (SPFA()) update(); printf("%d %d ",maxflow,mincost); return 0; }
Dinic算法求费用流那是不可以的呀!
- 网络流和二分图
求二分图匹配也是可以用网络流的呀,对于Dinic跑二分图复杂度可以证明是O(n sqrt (m))的,所以会快一点。
具体的做法就是左边的点都连一个大源点0,右边所有点都连一个大汇点N+1,令所有有向边的的权为1,然后跑0到N+1的最大流就是答案!
由于s到点左侧任意一点u的流量是1,所以u最多被选择一次。同理右边的点也最多被选择一次。于是这个图的网络最大流即为该二分图的最大匹配。