一、引入
拒绝采样,重要性采样的效率在高维空间很低,随维度增长其难度也指数型增长,主要适用于一维的采样。对于二维以上可以用马氏链。马尔可夫链蒙特卡洛采样方法就是在高维空间采样的方法。
马尔可夫链就是满足马尔可夫假设的一组状态序列$left { x_{t} ight }= ...,x_{t-2}, x_{t-1}, x_{t}, x_{t+1},...$,其中假设某一时刻状态$x_{t}$发生状态转移的概率只依赖于它的前一个状态$x_{t-1}$,这个就是马尔可夫假设:
$P(X_{t+1}mid X_{t-2}, X_{t-1}, X_{t}, X_{t+1} )=P(X_{t+1}mid X_{t})$
只要我们能知道系统中任意两个状态之间的转移概率,整个马尔可夫模型就知道了,定义转移概率为:
$P_{ij}=P(X_{t+1}=jmid X_{t}=i)$
转移概率衡量的是两个状态之间的转移几率,与时刻无关,仅涉及相邻的两个状态,如果系统中的状态有T种,那么转移概率可以构成一个T×T的转移矩阵P,马尔可夫链有收敛性质,就是说从任意一个初始分布出发,经过多次转移后,得到的分布是平稳的,不再变化的分布q,这个平稳分布q与初始分布无关,只与状态转移矩阵P有关。
接下来用一段代码说明这个问题:
matrix1=np.matrix([[0.9,0.075,0.025],[0.15,0.8,0.05],[0.25,0.25,0.5]],dtype=float) vector1=np.matrix([[0.3,0.4,0.3]],dtype=float) for i in range(100): vector1=vector1*matrix1 print('current round:',i+1) print(vector1)
输出最开始定义的matrix1和vector1,分别是转移概率和初始概率分布:

初始概率分布vector1表示的是在t=0时刻,$P(X_{0}=0)=0.3$,$P(X_{0}=1)=0.4$,$P(X_{0}=2)=0.3$,描述的是起初时刻,状态的分布情况,这里默认有三种状态,分别是1,2,3。
转移矩阵matrix1的位置11上的元素0.9表示的是:当前一时刻的状态$X_{t-1}$取1时,下一时刻的状态$X_{t}$取1的概率为0.9;
位置12上的元素0.075表示的是:当前一时刻的状态$X_{t-1}$取1时,下一时刻的状态$X_{t}$取2的概率为0.075;
可以用vector1*matrix1用矩阵乘法公式来计算一下,会得到一个形式和vector1一样的矩阵,有三个元素,每个元素表示的就是该时刻的状态分布情况:
根据矩阵乘法公式来计算一下下一时刻的状态分布的第一个元素为:(0.3*0.9+0.4*0.15+0.3*0.25),可以看出,它表示的是【不管上一时刻是取了哪个值,下一时刻状态为1的概率】,这个元素的计算考虑了上一个时刻的状态分布概率,比如0.3*0.9,这个乘积的含义就是上一时刻状态为1的概率是0.3,在上一时刻状态为1的条件下下一时刻状态仍为1的概率是0.9,注意这里的0.9是个条件概率;相乘就可以得到上一时刻状态为1,且下一时刻状态为1的概率,这里注意这是个联合概率分布。
输出一下整体的代码结果:
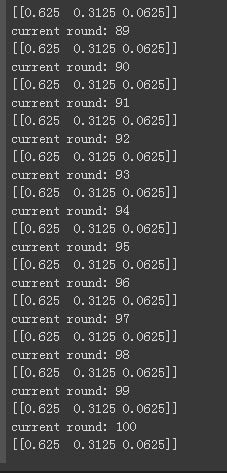
我们发现最后得到的分布基本是平稳不变的,即:状态取0和3的概率是0.625,状态取1的概率是0.3125。我们可以改变初始vector1,但是最终收敛的平稳分布依旧是不变的。这个就是马氏链的收敛。


我们的目标是希望从平稳分布q中进行采样。现在的问题如下:
- 什么样的马氏链可以收敛到一个平稳分布q?所有的马氏链都收敛吗?这个在截图中已有。
- 既然q只和转移矩阵P有关,我们要如何确定马氏链中的转移矩阵P,使得平稳分布是我们想要的q?在三中说明
- 我们具体要怎么从平稳分布中采样?这个在二中大体说明,在三中具体说明
二、怎么基于马尔可夫链采样?
假设我们有初始概率分布为$pi _{0}left ( x ight )$,基于$pi _{0}left ( x ight )$采样得到$x_{0}$;
然后基于条件概率分布$Pleft ( xmid x_{0} ight )$采样得到$x_{1}$;
基于条件概率分布$Pleft ( xmid x_{1} ight )$采样得到$x_{2}$;
当这个过程进行到第n个时刻时,假设此时达到平稳分布,即条件概率不再变化,如果我们的目标是要采m个样本的话,那么就从第n个时刻开始,再根据平稳分布$q$采m次得到m个样本,再做蒙特卡洛求和即可得到我们的目标期望。
这节只是为了引出下一节。在后面还会提到更具体的算法来说明如何从平稳分布里采样。
但是往往,我们只知道我们要从一个分布$q$中采样,这个$q$很难采我们才去找马尔可夫链,因为马尔可夫链进行到最后所得到的样本服从我们的目标分布$q$。但是$q$是多少主要取决于$P$,我们要怎么去确定$P$?这就是下一节会解决的第二个问题。
这里还要说明的就是,我们知道目标分布$q$的表达式,但这并不意味这我们可以直接从中采样,因为很难采,所以引入马尔可夫链,将直接采样方式转换为较为简单的条件概率分布采样。
三、马尔可夫链的细致平稳条件
上面代码部分说明了马氏链不断进行更新,最后会得到一个平稳分布,但是那是基于大量的计算才得到的结果。到底怎么样才算是一个平稳分布,现在给出定义:
如果非周期马尔可夫链的状态转移矩阵P和概率分布$pi(x)$满足$pi(i)P_{ij}=pi(j)P_{ji}$,那么就称pi(x)是状态转移矩阵P的平稳分布,再进一步对该式两边对状态i进行求和可得:
$sum_{i}^{infty }pi(i)P_{ij}=sum_{i}^{infty }pi(j)P_{ji}=pi(j)sum_{i}^{infty }P_{ji}=pi(j)$
上式证明了满足$pi(i)P_{ij}=pi(j)P_{ji}$的话,的确可以收敛。这个条件称为马尔可夫链的细致平稳条件,满足了这个条件的分布才能称为平稳分布。这个式子较为简洁的搭建了平稳分布和状态转移矩阵之间的关系。可以用来解决我们上面提到的第二个问题。
首先规定一个目标分布$pi(x)$是我们希望得到的平稳分布,也就是很难直接采样的分布$q$,和一个马尔可夫链状态转移矩阵$Q$,显然最开始它们是不满足细致平稳条件的:
$pi(i)Q_{ij} eq pi(j)Q_{ji}$
我们引入一个$alpha (ij)$,使得上式成立:
$pi(i)Q_{ij}alpha (ij)= pi(j)Q_{ji}alpha (ji)$
其中有:
$alpha (ij)= pi(j)Q_{ji}$
$alpha (ji)=pi(i)Q_{ij}$
所以我们得出一个结论:目标平稳分布对应的概率转移矩阵$P$,可以由任意一个状态转移矩阵$Q$,乘上一个接受率$alpha (ij)$得到;也就是说,想要得到的$P$,可以通过不正确的$Q$以一定的概率获得。所以我们在二、的基础上进一步细化我们马尔可夫链的采样过程如下:
1)初始拥有:任意转移矩阵Q,平稳分布$pi(x)$,转移次数$n_{1}$,所需样本数$n_{2}$
2)任意采样初始状态值$x_{0}$
3)$for t=0 to n_{1}+n_{2}-1$:
a)从条件概率分布$Qleft ( xmid x_{t} ight )$中采样得到样本$x_{*}$
b)采样$usim U[0,1]$
c)如果u< alpha (x_{t},x_{*})=pi(x_{*})Q(x_{*},x_{t}),就接受转移,即采样$x_{*}$,否则不接受,有$x_{t+1}=x_{t}$
为什么这里要采样一个均匀分布u样本点,来和接受率进行比较呢?因为接受率反应了一件事——原来的转移矩阵Q不符合我们的需求,它太大了,有一些样本不符合我们的所需,需要丢掉,但是怎么丢,就是看接受率,只有很少一部分的样本可以被我们选到。采样均匀分布体现了一个任意性,每个样本的接受率都是均匀的,意思是不存在有100个样本的接受率是0.9,而只有1个样本的接受率是0.1,均匀分布就是避免了这种情况,说明我们的样本集非常完整。就像如果要统计某病在人群中的发病率,我们最好控制变量,最好我们的样本集男女数目一样多,全国各省人的比例也和地区人数呈正比。
还有这里的转移次数$n_{1}$要怎么确定的问题,转移次数其实可以设置得大一些,因为我们采的样本是从第$n_{1}+1$次开始采的,前面都在使马尔科夫链达到平稳,只有平稳了我们才能开始收集样本。
这个方法也有缺点,就是如果我们的接受率很小$alpha (x_{t},x_{*})$,使得我们的大部分采样点都被拒绝了,这样的话,采样效率很低,也就是说会出现很多$x_{t+1}=x_{t}$的情况,采样样本中有很多相同的点,这不利于我们拿这些样本来做蒙特卡洛求和,因为很有可能这些样本对应的函数值很小,对整体起不到很大的作用。