一、简介
概率图模型(Probabilistic Graphical Model ,PGM)是用图来表示变量概率依赖关系的理论,结合概率论与图论的知识,利用图来表示与模型有关的变量的联合概率分布。图的每个节点(node)都表示一个随机变量,而图的边(edge)则被用于编码这些随机变量之间的关系,通常是条件概率。
对于一个K维随机变量$X=left [ X_{1},X_{2},...,X_{K}, ight ]^{T}$,它的联合概率分布是高维空间的分布,一般很难直接建模,特别是在我们不知道它们之间的依赖关系的时候。如果我们有三个二值随机变量,分别是$ X_{1}$, $X_{2} $,$X_{3}$,我们可以建立一个二维概率表来记录每一种取值的概率,因为有3个变量,每个变量有2种可能的取值,即我们有$2^{3}=8$种情况下的联合概率值,不过当我们知道前7个概率后,第8个概率直接用1-就可以计算出来,所以对于三个二值随机变量的联合概率分布,我们需要知道7个参数来表达它的联合概率分布。
随着随机变量的个数增加,所需参数数量会指数型增加,上一个例子是2的3次方,如果是10个随机变量就需要2的10次方-1个参数来说明这个联合随机概率分布。
有一种想法就是,如果我们能够知道其中几个随机变量之间的依赖关系,可以大大减少所需参数个数,大致可以这么想:如果我们知道当$ X_{1}=1$时,$X_{2}$只能取0,那么我们所需要的参数数量将会直接少一半。所以依赖于这种想法,有人提出了独立性假设,可以有效减少参数量,把K维随机变量的联合概率分布分解为K个条件概率的乘积:
$pleft ( x ight )=Pleft ( X=x ight )=pleft ( x_{1} ight )pleft ( x_{2}mid x_{1} ight )pleft ( x_{K}mid x_{1},...,x_{K-1} ight )=prod_{k=1}^{K}pleft ( x_{k}mid x_{1},...,x_{k-1} ight )$
当概率模型中的变量数量比较多的时候,其条件依赖关系也很复杂,有的随机变量可能会依赖1个或多个变量,可能有两个随机变量都依赖于同一个随机变量,为了表示这种复杂的关系,就引入了图结构,可以直观的描述随机变量之间的条件独立性性质,把一个复杂的联合概率模型分解成一些简单的条件概率模型的组合,对于一个非联通图,都存在多个条件独立性假设,可以根据条件独立性来将联合概率分解。比如下图就表示了,当已知X1时,X2和X3条件独立,且已知X2和X3时,X1和X4条件独立,且已知X4时,X2和X3不独立:

图模型有三个基本问题:
1.表示问题,就是给定一组随机变量的条件概率表示形式,怎么样画出图结构来描述变量之间的依赖关系。简称:给了式子怎么画图, 解决办法就是,如果是有向图,父节点表示条件,子节点表示当前的随机变量即可。
2.推断问题,就是在已知部分变量时,计算其他变量的后验概率分布。通常是已知可观测变量,求隐变量的后验概率分布的时候用到,其中还会有精确推断,近似推断,近似推断中又会涉及到一系列的采样方法的介绍。
3.学习问题,包括有图结构的学习和参数的学习,这里主要关注在给定图结构时的参数学习,即参数估计问题。很多机器学习模型都可以归结为概率模型,比如建模输入和输出之间的条件概率分布。
二、有向图模型
有向图模型又叫贝叶斯网络或信念网络,是指用有向图来表示概率分布的图模型。
贝叶斯网络定义:如果X的联合概率分布可以分解为每个随机变量的局部概率的连乘形式,则图结构就可以叫贝叶斯网络:
$pleft ( x ight )=prod_{k=1}^{K}pleft ( x_{k}mid x_{/k} ight )$
其中$x_{/k}$是$x_{k}$的所有父节点随机变量的集合。
我们知道,条件独立性是指有第三方的时候,双方独立。所以在图结构中,直接相连的两个节点不会构成条件独立,明显直接相连的二者不会因为任何其他人的出现而断开与彼此的联系,我们可以认为它们俩的感情很好,谁都不能拆散;
但是如果有两个节点,经过了第三个节点而产生了一条有联系的路径,它们之间有可能达到条件独立,也就是说,第三者干点什么事,就可能让本来有联系的双方老死不相往来了,没办法,谁让它们俩之间的联系是通过第三方呢?
以下简单讨论常用情况,详细的另开文章:


贝叶斯网络有局部马尔可夫性质:每个随机变量在给定其父节点的情况下,与它的非后代节点条件独立,也就是说,只要给定了一个节点的所有父节点,那么这个节点就和其他的既不是它的父节点也不是子节点的其他节点独立。
1.sigmoid信念网络
引入条件独立性假设,把高维随机变量之间的复杂关系降低,减少了参数量,但是替代其的是很多的条件概率,我们很贪心,希望进一步的更简单的去计算这些条件概率,于是我们可以用simoid函数来建模图模型中的条件概率。(看到这里的时候我在想,不是说高斯概率可以很好的模拟任意分布嘛,为什么要用sigmoid而不用高斯?),所以,建模如下:
$pleft ( x_{k}=1mid x_{/k}; heta ight )=sigma left ( heta _{0}+sum heta _{i}x_{i} ight )$
其中,$ heta _{i}$是我们要学习的参数,假设变量$x_{k}$的父节点有M个,如果使用我们最开始说的表格记录法来记录这个条件概率的话,需要2的M次方个参数,使用信念网络则只需要M+1个参数,且即使父节点增加了,复杂度也不会是指数型的增长。如果对不同变量的条件概率都用同一个参数化模型来模拟,那么参数量就更加少了。
2.朴素贝叶斯
条件概率,独立。就会想到机器学习中最简单的朴素贝叶斯分类器,它的朴素之名就来源于在给定Y的情况下X的各个特征之间是条件独立的,而且Y和X都是随机变量。所以朴素贝叶斯是个生成模型而不是判别模型,判别模型中的条件只是个变量,而不是随机变量,没有随机性。
3.隐马尔可夫模型
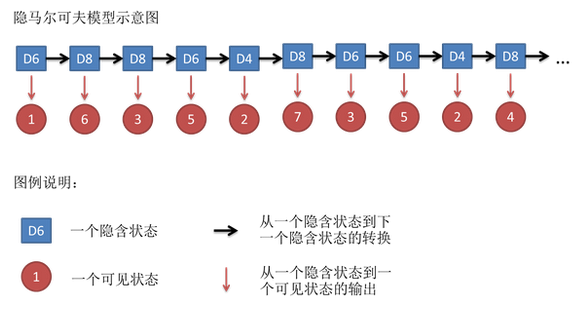
把蓝色隐含状态视为y1,y2,y3..,红色可见状态视为x1,x2...,然后隐马尔可夫的联合概率按照上面讲的方法可以写成:
$pleft ( x,y; heta ight )=prod_{t=1}^{T}pleft ( y_{t}mid y_{t-1}, heta_{s} ight )pleft ( x_{t}mid y_{t}, heta_{t} ight )$
有向图中不管是看图写公式还是看公式画图都算比较简单的。学了概率图模型后,再理解隐马尔可夫就比较容易了。
三、无向图模型
无向图模型又叫马尔可夫随机场或马尔可夫网络,是用无向图来描述具有局部马尔可夫性质的随机向量X的联合概率分布的模型。前面说有向图的贝叶斯网络的时候,也说到过贝叶斯网络有局部马尔可夫性质,但是贝叶斯网络是有向图,其中描述给定的条件节点是某个随机变量的父节点,然而在马尔可夫随机场中是无向图,没有父子节点之说,只有邻居节点。所以我们把这里的局部马尔科夫性质换一种表述:一个随机变量在给定它的邻居的情况下独立于其他所有变量,用式子表达如下:
$pleft ( x_{k}mid x_{/k} ight )=prod_{k=1}^{K}pleft ( x_{k}mid x_{N(k)} ight )$
$x_{N(k)}$就是$x_{k}$的邻居节点,而$x_{/k}$是除了$x_{k}$以外的所有节点。也就是说$x_{/k}$包括$x_{k}$的邻居节点$x_{N(k)}$。我们可以看到左式和右式相等,右式的条件部分比左式减少的部分就是非邻居节点被抛去了,也就是说这个式子表达的含义就是在给定邻居节点的时候,非邻居节点和原节点$x_{k}$相互独立。这就是无向图的马尔可夫性质。
因为无向图没有方向,我们很难像有向图一样,找到父节点就是找到了条件,所以不能用有向图的方法来构造图和数学式子之间的关系。这种看图写公式的我们可以叫做概率分解,因为整个图模型表达的就是一个联合概率分布,不管是有向图还是无向图,它画出来的目的或存在的意义都是让多个随机变量之间的条件关系更加清楚,也就是把联合概率分布分解成一个个的条件概率相乘的形式。现在的无向图的难点在于,没有父节点这种说法,我们怎么找条件。
好在无向图起码也有一个局部马尔可夫性,由这个性质出发思考,一个随机变量在给定它的邻居的情况下独立于其他所有变量,首先这个邻居肯定是和随机变量不是独立的,毕竟都直接相连了,然后这个随机变量X和其他所有变量就条件独立了,这个其他所有变量是什么,既然和X不直接相连,但是又确实和X在同一个图内,而且又不是X的邻居节点,那么就是X的邻居的邻居节点。那如果X没有邻居的邻居呢,也就是这是一个全连通图,那就没什么可说的了,不存在谁和谁条件独立了,大家都是两两相连的,都是一家人,关起门来好商量,一家人的联合概率就由一家人独自解决,具体怎么办呢,那就看团里的人怎么商量了;与团相对,还有最大团的概念,意思就是说,比如三个节点两两相连,相亲相爱,这时候其中的一个节点A说,我要带一个新节点D来一起玩,A很喜欢D,但其余两个节点BC都不喜欢D,当A不在的时候,D和B或C相处得都不愉快,不能成一家人,没办法关门商量,只好把D赶走才行。
有一个定理叫Hammersley-Clifford,意思就是如果一个联合概率分布满足局部马尔可夫性质,那么联合概率就可以拆解成最大团上非负函数的乘积形式,这个非负函数通常是定义在最大团上的势能函数,势能函数就是一个衡量能量E与势能phi的函数,物理里,能量越高,势能越低。如果吧能量理解为以前高中学的动能,小球从高处速度为0的时候开始落下,重力势能减小,动能增大,因为势能转化为动能了。这个势能函数应该就想表达,小球速度越快(动能越大),重力势能就越小。具体公式如下:
$pleft ( x ight )=frac{1}{Z}prod_{cin C}phi left ( x_{c} ight )$
$phi left ( x_{c} ight )=expleft ( -E_{c}left ( x_{c} ight ) ight )$
其中的Z就是用来概率归一化的,称为配分函数,它的计算复杂度是指数级的,所以推断和参数学习的时候是个坎。
上面这个公式也叫吉布斯分布,根据Hammersley-Clifford,无向图模型和吉布斯分布等价。因为吉布斯分布一定满足马尔可夫随机场的性质,且马尔科夫随机场的概率分布一定可以表示成吉布斯分布。如果用吉布斯分布+势能函数公式来表达无向图模型的话,这种分布还可以叫玻尔兹曼分布,而任何一个无向图模型表示的联合概率分布都可以表示成玻尔兹曼分布的形式。
常见的无向图模型有:
1.对数线性模型/最大熵模型
对数线性模型其实就是把线性模型放在指数位置上,再加上一个归一化系数就好。之所以叫对数线性模型是因为把指数去掉之后,概率部分多了一个log;同时也叫最大熵模型,因为这种模型学习的原则就是让熵最大。因为加上归一化系数后,整体式子看着就很像把线性模型套进softmax函数里,所以又叫softmax回归模型,但本质上是做分类的。而且如果用对数线性模型来直接建模条件概率的话,其中的y只代表取值,而不是随机变量。这里只放公式,详细笔记放在机器学习分类里:
$p(ymid x; heta )=frac{1}{Z(x; heta ))}exp( heta ^{T}f(x,y))$
2.条件随机场
条件随机场是直接建模条件概率的无向图模型,与上一个对数线性模型中y代表取值不同,这里的y是随机变量,所以不能直接套用线性模型放在指数部分,而是要进行因子分解,也就是把许多的y拆解成最大团,用势能函数来替代线性模型放在指数部分。就像前面讲到的吉布斯分布一样。
其条件概率分布为:
$p(ymid x; heta )=frac{1}{Z(x; heta ))}exp(sum_{cin C}^{ } heta _{c}^{T}f_{c}(x,y_{c}))$
常用的条件随机场是链式结构,称为线性链条件随机场(CRF):
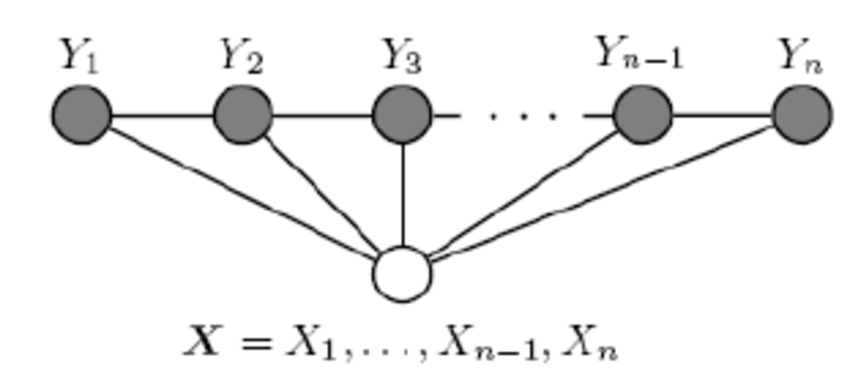
其条件概率为:
$p(ymid x; heta )=frac{1}{Z(x; heta ))}exp(sum_{t=1}^{T} heta _{1}^{T}f_{1}(x,y_{t})+sum_{t=1}^{T} heta _{2}^{T}f_{2}(x,y_{t},y_{t+1}))$
其中f1表示的是状态特征,也就是x和某个位置上的y构成的最大团的势能函数,主要和这个y的位置t有关;f2表示的是转移特征,主要和两个y他们的相对关系有关。这里不再把f称为势能函数,而是称为特征,含义是“满足某种条件时表现出来的特征”,在高维空间中,两个随机变量之间的关系很难简单的用条件刻画,更广泛的理解,可以称为两个随机变量有关系,它们有关系的时候会表现出某种特征被我们捕捉到。在后面讲玻尔兹曼机的时候会提到类似的思想。
四、有向图无向图转换
主要关注将有向图转化为无向图,转化的原则就是如果有几个向量都相关,那么就要把它们全部归属到一个团中,即加上连边即可。但是这样会丢失一些独立性,本身独立的两个随机变量会因为增加了连边而变得不再独立。