摘要:n阶方阵A满足AX=λx,λ为 矩阵A的特征值,x为特征值对应的特征向量。

一.乘幂法(求模最大特征值及对应特征向量)
设矩阵A有n个相性无关的特征向量x1,x2,x3,.....xn,相应的特征值λ1,λ2,λ3,.....λn(由大到小排列)。
迭代法引入:上一章学了迭代法求解线性方程组Ax=b的解,给定任一 的初始值v0,不断迭代可以得到Ax=b的解。同理,给定任一非零的n维向量v0,不断迭代可以 得到矩阵A的特征向量 ,
,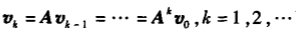
对于初始向量v0可以由A的n个线性无关的特征向量表示: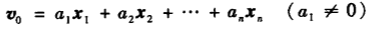
带入迭代方程中:
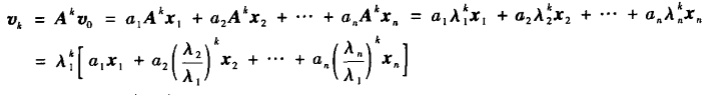
当迭代次数k趋近于无穷大时,可得到最大特征值λ1对应的特征向量a1x1(与x1线性相关)
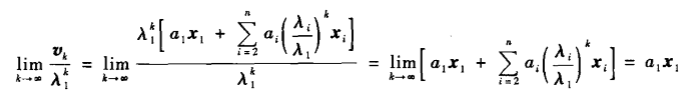
同理,当迭代次数趋近于无穷大时,可得到绝对值最大的特征值,λ1
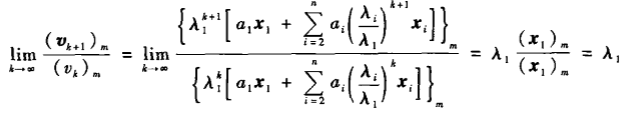
其中,m表示向量中的绝对值最大的那个元素值
如何利用迭代法求解按模最大特征值和特征向量

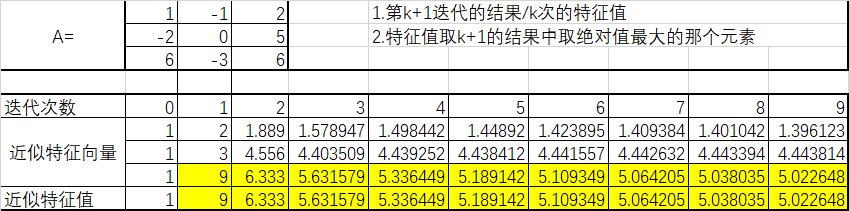

说明:
1.初始值:我们给定初始值x0=[1,1,1]^T,取特征值1
2.第一次迭代:
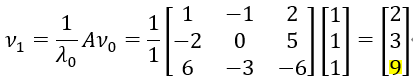 对应的近似特征值取:
对应的近似特征值取: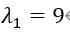
3.第二次迭代:
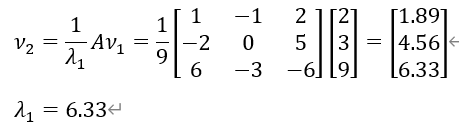
二.改进乘幂法
这个规范化处理的目的:防止数据溢出或是数据消失

从上面可以看出,改进乘幂法即是每次迭代出的特征向量都进行一次规范化处理