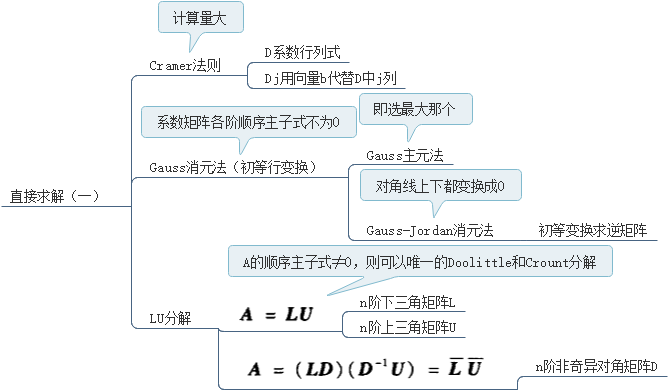
1.Cramer法则:
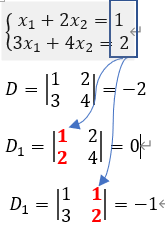
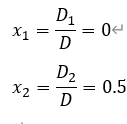
其中D是系数矩阵A对应的行列式,D1是用1,2代替第一列的数值,D2是用1,2代替第二列的数值。
特点:计算逻辑简单,计算量大。只能计算系数矩阵A是方阵的函数,并且A的行列式不能为0.
2.Gauss消元法(初等行变换)

特点:系数行列式值不变,顺序主子式的值不变。因此,使用该方法的条件是:系数矩阵A的 各阶顺序主子式不为零。
缺点:当aii=0,就不能求解;在消元过程中,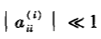 时,舍入误差扩散,导致误差过大
时,舍入误差扩散,导致误差过大
3.Gauss主元素法
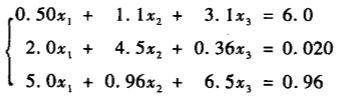
列主消元法:【每一次消元,都把aii最大的行作为基础】

特点:能够降低计算误差,不改变矩阵的列位置
4.全主消元法:
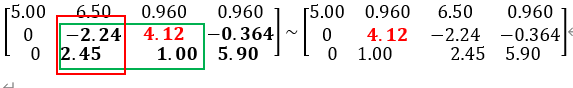
列主消元法实在红色框内寻找最大值,并且调整行的位置。
全主消元法则是在绿色框内寻找最大值,这将伴随解位置的变化【如,原本x3的系数在第三列,调整之后,就在第二列了,最后的解位置也需要随之调整】。
特点:相比于列主消元法,从未消部分中,寻找最大值,列位置变化(解的位置变化)
5.Gauss-Jordan消元法【方阵求逆】
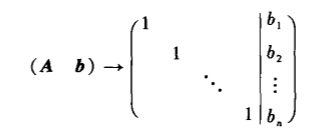
特点:能够直接得出解,省去带入过程,计算量与消元法计算量相当。
6.矩阵的LU分解:
补充:初等矩阵左乘矩阵A,相当于矩阵A的行变换,如下式所示。
变换后行列式的值不变,顺序主子式的值不变。
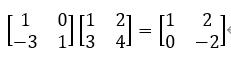
第一次:行变换
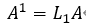
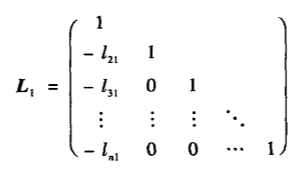
第k次:行变换
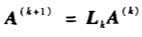
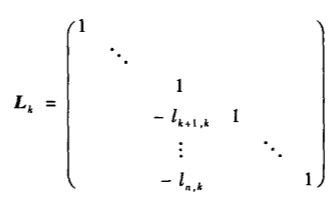
如何确定初等矩阵的元素值:
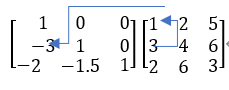
L的第一列元素确定公式: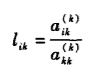
LU消元法:实则是消元法的乘法形式,也是进行初等航变换,化解成上三角或下三角矩阵
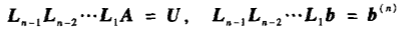
- Doolittle分解:L为单位下三角矩阵(对角元素为1)
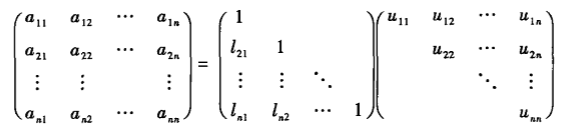
计算过程:
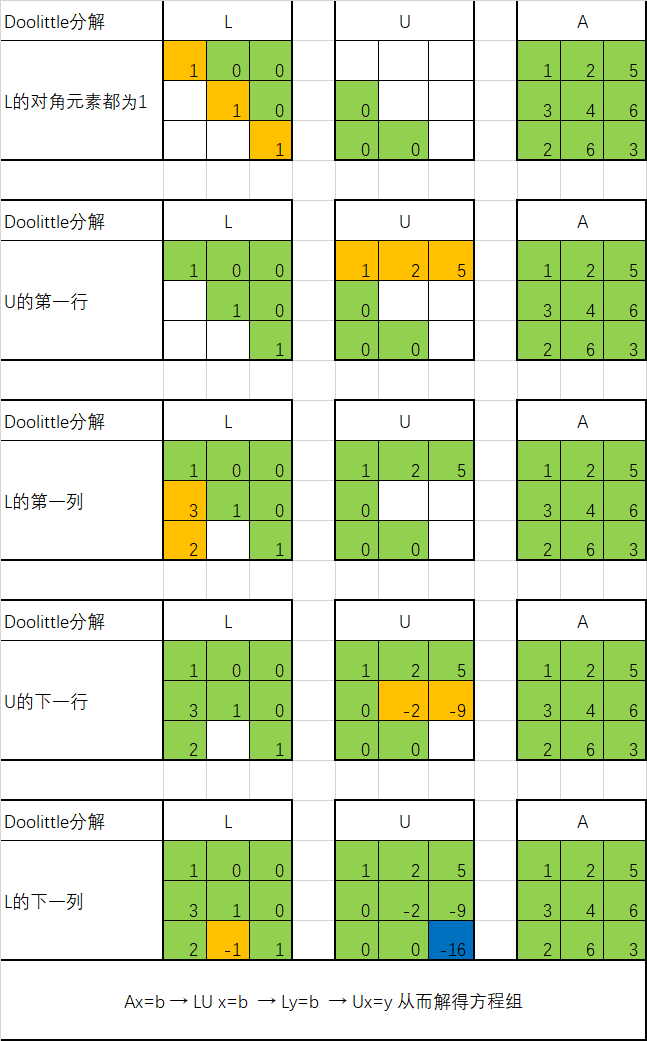
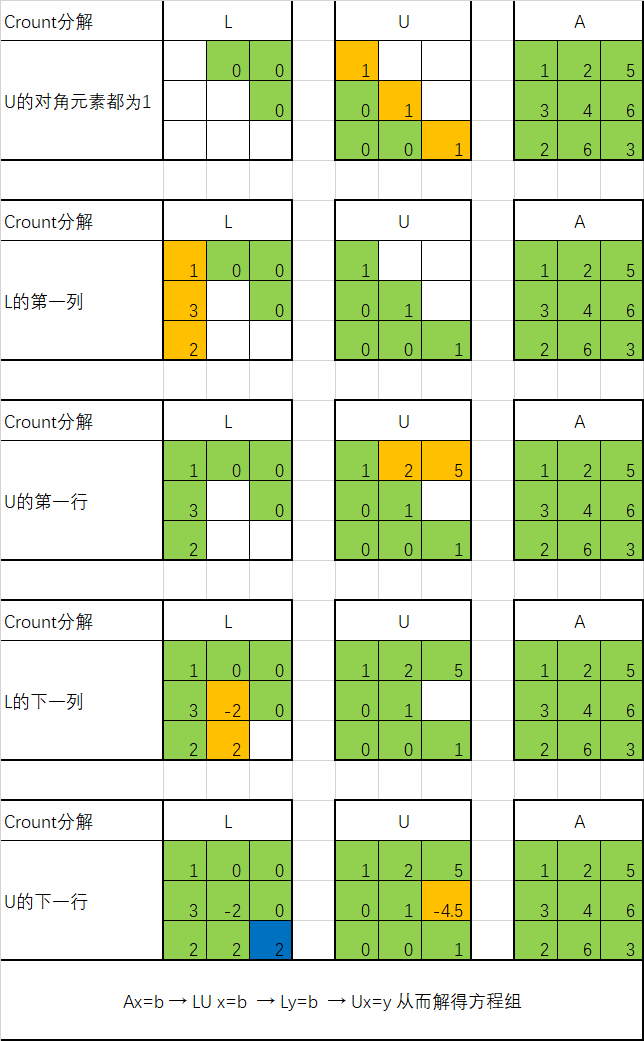
- Crount分解:U为单位上三角矩阵
计算过程: