小 Y 的背包计数问题
题目:
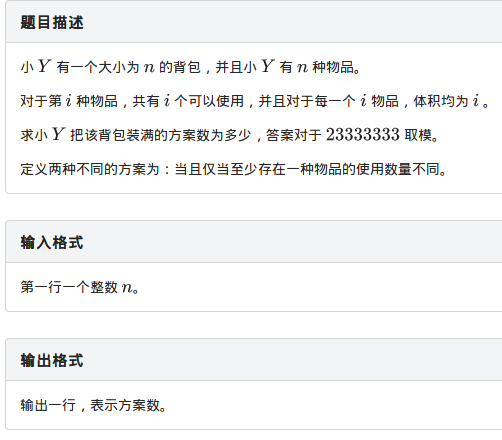
非常小清新的题目描述,就是一个很简单的背包,直接(n^2)搞起。
等会,数据范围(1e5????)
这咋搞啊?
神犇:(nsqrt n)搞。
以上是我看到这题时候的心里过程,可以无视掉
这道题是一个很厉害的dp和卡常技巧相结合的题,虽说这道题最优复杂度是(nsqrt n)但是只要写丑,实际复杂度会到(3e7)以上,加上那么多取膜和(CCF)的老爷机,直接(T)飞。
先说思路:
定义两个(dp)数组,不妨设他们为(dp)与(f)吧。
(dp[i][j])表示只考虑前(sqrt n)个数,前(i)个数,每个数选某些个,占据背包体积为(j)的方案数。
(f[i][j])表示(sqrt n +1)~(n)这些数中,任意选(i)个数,占据背包体积为(j)的方案数。
然后我们只要保证得出这两个数组中的值的过程不超过(nsqrt n)的复杂度就行了。
先考虑第一个转移:
比较显然有:(dp[i][j]=sumlimits_{k}^{i imes k<=j}dp[i-1][j-k imes i])
注意到这样转移的时候需要枚举(i),(j),(k)三个变量,复杂度成了(n^2 sqrt n)了,所以需要优化:
考虑前缀和优化:每枚举到一个(i),先(O(n))算出(sum)数组,(sum[j])表示(dp[i-1][j],dp[i-1][j-i],dp[i-1][j-2 imes i]……)的和,然后转移的时候就(dp[i][j]=sum[j]-sum[j-i imes (i+1)])(原因是(i)这个物品最多被选(i)次,而计算(sum)的时候有可能把超过(i)件的方案数也统计了过来,所以减一下)。
第二个转移:
运用整数划分的思想,每次加数要么加(sqrt n +1)要么把当前的所有数(+1),就可以拼成所有情况。
(f[i][j]=f[i][j-i]+f[i-1][j-sqrt(n)-1])
因为每个数都是大于(sqrt n)的,所以最多选(sqrt n)个数,(i)的枚举边界是这个。
注意这里的j枚举需要从((sqrt n +1)*i)开始枚举,算一个小小的剪枝,但是能把时间从(1.2s)剪到(0.9s)。
然后综合统计一下,注意判断边界(比如前(sqrt n)个数拼出(n)后面那些数拼出0的情况)。
还有记得码写的好看一点。
码:
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
const int mod=23333333;
int dp[320][maxn],sum[maxn],f[320][maxn];
int n;
int main(){
scanf("%d",&n);
register int sqn=sqrt(n);
dp[0][0]=1;
for(register int i=1;i<=sqn;i++){
for(register int j=0;j<=n;j++){
sum[j]=(sum[j-i]+dp[i-1][j])%mod;
}
for(register int j=0;j<=n;j++){
dp[i][j]=sum[j];
if(j>=i*(i+1))dp[i][j]=(1ll*dp[i][j]-sum[j-i*(i+1)]+mod)%mod;
}
}
f[0][0]=1;
int ans=dp[sqn][n];
for(register int i=1;i<=sqn;i++){
for(register int j=(sqn+1)*i;j<=n;j++){
f[i][j]=(1ll*f[i-1][j-sqn-1]+f[i][j-i])%mod;
ans=(1ll*ans+1ll*f[i][j]*dp[sqn][n-j])%mod;
}
}
printf("%d
",ans);
return 0;
}