只考虑村民边，然后每个村民边求联通块，最后加狼边，看看两个端点在不在一个联通块里就可以了。 比赛的时候有点坑，思路正确，写歪了……
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 50;
vector<int> g[maxn];
int fa[maxn];
int in[maxn];
int lang[maxn];
int cnt[maxn];
void dfs(int u, int root) ///同属一个根
{
fa[u] = root;
for(int i = 0; i < g[u].size(); i++)
{
dfs(g[u][i], root);
cnt[u] += cnt[g[u][i]];
}
}
int main()
{
int T; scanf("%d", &T);
while(T--)
{
int n; scanf("%d", &n);
for(int i = 1; i <= n; i++) g[i].clear(), fa[i] = 0, in[i] = 0, cnt[i] = 1, lang[i] = 0;
for(int i = 1; i <= n; i++)
{
int v;
char s[15];
scanf("%d %s", &v, s);
if(s[0] == 'v')
{
g[v].push_back(i);
in[i]++;
}
else lang[i] = v;
}
for(int i = 1; i <= n; i++) if(!in[i]) dfs(i, i);
int ans = 0;
for(int i = 1; i <= n; i++)
{
if(!in[i] && (fa[lang[i]] == i)) ans += cnt[lang[i]];
}
printf("0 %d
", ans);
}
return 0;
}
/*423
6
2 v
3 v
4 v
5 v
3 w
4 v
*/
这题首先要找到规律：
$gcd(2^{a}-1,2^{b}-1)=2^{gcd(a,b)}-1.$
这个看大家都没有证明，我看了dls的讲解后，还有问学长，给出下面证明：
设$a < b;$
$gcd(2^{a}-1,2^{b}-1)$
$=gcd(2^{a}-1-(2^{b}-1) imes 2^{a-b},2^{b}-1)$ （这个和正常的辗转相除一样：$gcd(a,b)=gcd(a-b imes lfloor a / b floor , b)$）
整理得：
$=gcd(2^{a-b}-1,2^{b}-1)$
继续：
$=gcd(2^{a-2 imes b}-1,2^{b}-1)$
……
$=gcd(2^{a\%b}-1,2^{b}-1)$
然后这时候$a\%b < b$，再像正常的那样反过来继续$gcd$就行，直到一边$a\%b=0，2^{0}-1=0，$那么最后的$gcd$就是$2^{g}-1$，而$g=gcd(a,b)$，证明完毕。
而$gcd(fib(a),fib(b))=fib(gcd(a,b))$，这位老铁给出了证明。
而最后化简完求的是：$2^{gcd(f[x1],f[x2],……,f[xk])}=2^{f[gcd(x1,x2,……,xk)]}。$
令$d=gcd(x1,x2,……,xk)，$相当于$d|x1，d|x2，……，d|xk.$
对$x1,x2,……,xk$求和，得$frac{x1+x2+……+xk=n}{d}.$ 问题演化为：有k个数，每个数都可以除以d，并且k个数的和是n，问这样的数的组合有多少种？
利用隔板法：可以先把n分成n/d份，然后得出组合数$C(n/d+k-1,k-1)$。
这时，我们令f[d]表示 $d | gcd(x1,x2,……,xk)$的方案数。
令g[d]表示$d=gcd(x1,x2,……,xk)$的方案数。
则$f[d]=C(n/d+k-1,k-1)$。
而$g[d]=f[d]-sum_{d|x} g[x]$，从大到小枚举因子就可以了。
不太懂f[d]和g[d]的关系，我们可以举个例子，假如$n=12，k=3，$首先枚举d=1，那么f[d]不仅包括$gcd=1$的，还包括$gcd=2、3、4、6、12$的，所以我们只算$gcd=1$的，减去其他的就可以了，最后答案再乘以$2^{fib[d]}-1$就可以了。
因为指数特别大，最后再利用欧拉降幂公式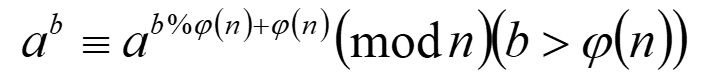
不要求a和n互质。
这里n是质数，$a^{varphi(n)} \% n=1$，根据费马小定理，所以可以不用加后面。
#include <bits/stdc++.h> using namespace std; const int maxn = 2e6 + 50; typedef long long ll; int fac[maxn]; int sing[maxn]; int inv[maxn]; int f[maxn / 2]; int g[maxn / 2]; int fib[maxn / 2]; const ll mod = 1e9 + 7; void init(int n) { fac[0] = fac[1] = sing[0] = sing[1] = inv[0] = inv[1] = 1; for(int i = 2; i <= n; i++) { fac[i] = (ll)fac[i - 1] * i % mod; sing[i] = (ll)(mod - mod / i) * sing[mod % i] % mod; inv[i] = (ll)inv[i - 1] * sing[i] % mod; } } ll quick_pow(ll a,ll n) { ll res = 1; while(n) { if(n % 2LL) res = res * a % mod; n >>= 1LL; a = a * a % mod; } return res; } vector<int> yue; int main() { duipai(); init(2e6 + 10); int T; scanf("%d", &T); fib[0] = 0, fib[1] = fib[2] = 1; ll fain = mod - 1; int early = maxn; for(int i = 3; i <= (1e6 + 5); i++) { fib[i] = fib[i - 1] + fib[i - 2]; if((ll)fib[i] > fain) { if(maxn == early) early = i; fib[i] = (ll)fib[i] % fain; } } while(T--) { yue.clear(); int n, k; scanf("%d %d", &n, &k); for(int i = 1; i <= n; i++) { f[i] = 0; g[i] = 0; if(n % i == 0) { yue.push_back(i); f[i] = (ll)fac[n / i + k - 1] * inv[k - 1] % mod * (ll)inv[n / i] % mod; } } ll ans = 0; for(int i = yue.size() - 1; i >= 0; i--) { int d = yue[i]; g[d] = f[d]; for(int j = i + 1; j < yue.size(); j++) { int x = yue[j]; if(x % d == 0) g[d] = ((ll)g[d] + mod - (ll)g[x]) % mod; } } for(int i = 0; i < yue.size(); i++) { int d = yue[i]; ll mi = fib[d] + (d >= early ? fain : 0); ans = (ans + (ll)g[d] * ((quick_pow(2LL, mi) - 1LL + mod) % mod) % mod) % mod; } ans = (ans * quick_pow((ll)f[1], mod - 2)) % mod; printf("%lld ", ans); } return 0; }
这题算是Lucas定理的应用了。
看dls和题解，整理一下自己的思路。
首先应用Lucas定理，$C(n,m)\%p=C(n/p,m/p)*C(n\%p,m\%p)\%p$，将大组合数通过递归来转换，比如n转换成p进制为$n=2301,p=4$，$m=0131$,那么$C(n,m)=C(2,0) imes C(3,1) imes C(0,3) imes C(1,1)$，所以要想在矩阵中不为0，对应每一个子组合数都应该$n>=m$。 然后$(i,j)$为1的话，代表从$i$到$j$有一条路径，$K$次方对应走$K$步的方案数。
我们看给出的方程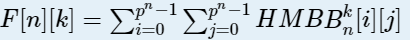
，正好可以把$i$和$j$拆成$n$位，我们要保证走$K$步可行，就得保证$i$中的$n$位中的每一位都不小于$j$中的每一位。
每一位单独考虑，我们用$p-1$个隔板去隔$K$步，走K步会有$K+1$个数，这样得到的组合数是$C(K+p,p-1)$,$n$位就是$C(K+p,p-1)^{n}$。
#include <bits/stdc++.h> using namespace std; typedef long long ll; const int maxn = 2e6 + 50; const ll mod = 1e9 + 7; //线性素数筛 int prime[maxn] = {0},num_prime = 0; int isNotPrime[maxn] = {1,1}; void is_prime(int N) { for(int i=2;i<N;i++) { if(!isNotPrime[i]) { prime[num_prime++] = i; } for(int j=0;j<num_prime&&i*prime[j]<N;j++) { isNotPrime[i*prime[j]] = 1; if(!(i%prime[j])) { break; } } } return; } int fac[1400000], sing[1400000], inv[1400000]; void init(int n) { fac[0] = fac[1] = sing[0] = sing[1] = inv[0] = inv[1] = 1; for(int i = 2; i <= n; i++) { fac[i] = (ll)fac[i - 1] * i % mod; sing[i] = (ll)(mod - mod / i) * sing[mod % i] % mod; inv[i] = (ll)inv[i - 1] * sing[i] % mod; } } ll quick_pow(ll a, ll n) { ll res = 1; while(n) { if(n % 2) res = res * a % mod; n >>= 1; a = a * a % mod; } return res; } int main() { is_prime(1e6 + 5e5); //printf("%d ", prime[100000 - 1]); init(1e6 + 4e5); int T; scanf("%d", &T); while(T--) { int c, n, k; scanf("%d %d %d", &c, &n, &k); int p = prime[c - 1]; ll ans = 0; for(int j = 1; j <= k; j++) { int down = j + p; int up = p - 1; ll q = (ll)fac[down] * inv[up] % mod * inv[down - up] % mod; // printf("%d %d %lld ", down, up, q); if(q == 1LL) { ans = (ans + n) % mod; } else { ans = (ans + (quick_pow(q, n + 1) - q + mod) % mod * quick_pow(q - 1, mod - 2) % mod) % mod; } } printf("%lld ", ans); } return 0; }