一、对比
和\(Acwing\) \(323\). 战略游戏这题非常类似,但又有些不同
\(Acwing\) \(323\). 战略游戏在一条道路的两个结点至少有一个是放的,而这题不一定,比如
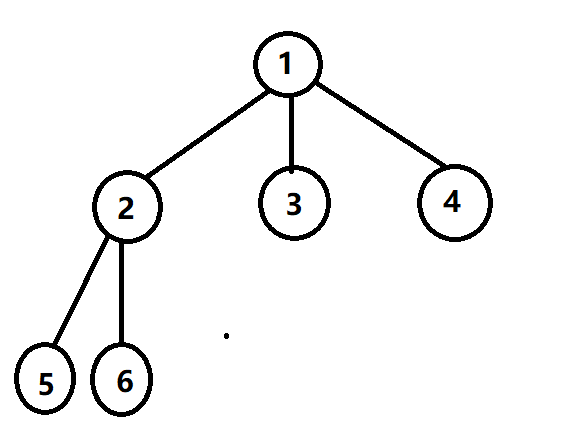
我们可以在\(3\),\(4\),\(5\),\(6\)号点放,其他各点都不放。这样边\(1-2\)的两个端点都没有守卫,这就和\(Acwing\) \(323\). 战略游戏这题不同了
二、思路
不过稍微观察可以发现,\(Acwing\) \(323\). 战略游戏这题的切入点是边,而本题的切入点是宫殿,也就是树上的结点。那么可以用放不放这个状态上增加一个状态,即
-
不放守卫
1.父结点放了,记f[u][0]
2.子节点放了,记f[u][1] -
放置守卫,记
f[u][2]
其中u为当前的结点,这样就可以涵盖整个状态空间
状态描述这么划分,其实是存在重叠情况的,比如
u结点不放守卫,它的父结点放了守卫,而且,它的子结点也放了守卫,这种情况是可能存在的。这样并不奇怪,因为我们最终要求的是最小值,只要不遗漏某种情况,最终的最小值是一样的。
有了状态表示,接下来\(j\)就是推导状态转移了,记\(j\)为\(u\)的子结点,那么
- \(f[u][0]=\sum_{j=0}^{u}min\left \{f[j][1],f[j][2] \right \}\)
含义:当前结点u不放且被父节点看到,那么子结点j只能放或者被其子结点看到。因为u不放所以不能拿f[j][0]来更新
- \(f[u][1]=f[k][2]+ \sum_{j=0,j \neq k}^{u}min\left \{ f[j][1],f[j][2] \right \}\)
含义:当前结点u不放,u的子结点k放了,u的其他子结点j放(f[j][2])或者不放(即f[j][1])。没有f[j][0]的原因也是因为u不放,且需要枚举k。
- \(f[u][2]=\sum_{j=0}^{u}min\left \{ f[j][0],f[j][1],f[j][2] \right \}\)
含义:当前结点放了,那么子结点取哪种状态都可以
\(1\),\(3\)实现起来比较容易,至于\(2\)的实现,做如下解释:
预求f[u][1],代表含义:
场景:u不放卫兵,靠u的子结点给它守护,一定有某个子结点j,放置卫兵,其它子结点不放卫兵
结果:所有方案计算代价的最小值。
这个东西怎么求?
(1)假设是j号子结点放了卫兵,它可以取得的最小代价是确定的:f[j][2],并且,由于上面的循环中已经计算过f[j][2],所以直接用就行。
(2)其它非j号子结点不放卫兵情况下的最小代价是所有这些子结点的最小代价和: \(S_{nj}= sum { min(f[k][1],f[k][2]) }\) \(j≠k\)
(3)\(f[u][1]=min(f[u][1],f[j][2]+ S_{nj})\) //j号不放情况下其它子结点的最小代价和+j号的代价
(4)如何求\(S_{nj}\)呢?在确枚举每个j的时候,二次循环所有子结点,再排除掉j计算\(S_{nj}\)?那样就太笨重了,没必要,用一点点数学思想即可:
- 先求出所有子结点的最小代价总和 \(sum=\sum_{j=1}^{u}min(f[j][1],f[j][2])\)
- 枚举
u的所有子结点,假设当前遍历到的j就是我们想要的那个,那么\(sum-min(f[j][1],f[j][2])\)就是除j外其它结点的最小代价值和。 - 再加上自身的代价\(f[j][2]\),整体取最小值。这样所有子结点枚举完,最终\(f[u][1]\)中保存的就是答案。
- 我们很惊奇地发现,
f[u][0]就已经计算过了这个sum,可以拿f[u][0]来代替sum,但为了语义明确,使用sum来表示更合理
二、实现代码
#include <bits/stdc++.h>
using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 1510;
int n;
int h[N], e[N], ne[N], idx, w[N];
int f[N][3];
bool st[N]; //是不是树根,false:是,true:不是
//链表
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void dfs(int u) {
//u结点不放卫兵,由u的父结点负责看管(好爸爸),u结点付出代价为0,可以省略
f[u][0] = 0;
//u结点不放卫兵,由u的某一个子结点负责看管,其它子结点取min(f[j][1],f[j][2])
f[u][1]=INF;
//u结点放置卫兵,代价初始化w[u]
f[u][2] = w[u];
int sum = 0;
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
dfs(j);
f[u][0] += min(f[j][1], f[j][2]);
f[u][2] += min(min(f[j][0], f[j][1]), f[j][2]);
sum += min(f[j][1], f[j][2]);
}
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
f[u][1] = min(f[u][1], sum - min(f[j][1], f[j][2]) + f[j][2]);
}
}
int main() {
//初始化邻接表
memset(h, -1, sizeof h);
cin >> n;
for (int i = 1; i <= n; i++) {
int x, m;
cin >> x >> w[x] >> m;
while (m--) {
int y;
cin >> y;
add(x, y);//有向图
st[y] = true; //标识不是根
}
}
//找到根
int root = 1;
while (st[root]) root++;
dfs(root);
//root没有父结点,代价最小值肯定在剩余两种状态中取min
cout << min(f[root][1], f[root][2]) << endl;
return 0;
}