一、题目描述
给定一个 \(8×8\) 的棋盘,棋盘的每个小方格都有一个权值 \(w_x,w_y\)
每次我们可以对棋盘进行一次横或竖切,将棋盘分成两块矩形的子棋盘
分割完一次后,我们可以选择两个子棋盘中的一个再继续递归操作。
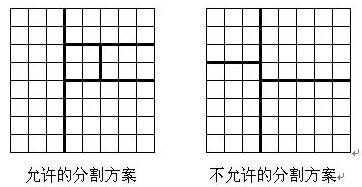
可以发现题目中给的这个图片,右边这个并不是递归下去做的:他对第一次分割的两个矩形又分别进行了分割(题目要求我们只能保留一个继续分割)
现需要把棋盘按照上述分割方案,分成 \(n\) 块(\(n−1\) 次划分操作)
求一个划分方案,使得各子棋盘的 总分的均方差最小
二、试题解析
做高中数学题遇到方差的时候,一般需要化简
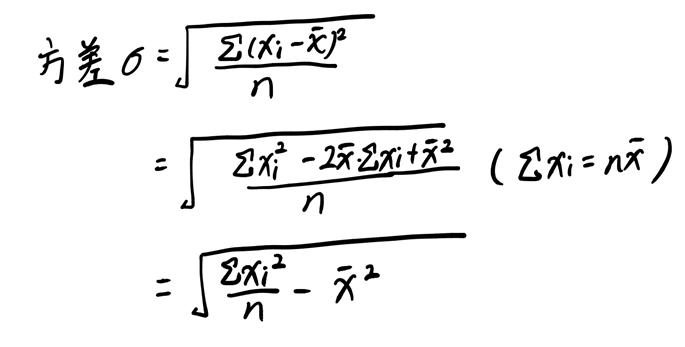
但本题不需要化简,也可以直接来做,但有的题目不化简不能做。
不难发现,递归操作会有很多冗余的重复计算,于是我们可以采用 记忆化搜索 进行优化
\(f[x_1,y_1,x_2,y_2,k]\) 表示这个区间在剩余\(k\)刀的情况下,可以获取到的计算公式最大值
关于如何枚举矩阵的分割
由于我们这里记录矩阵的状态是通过他的 对角顶点 记录的,因此分割是我们也可以通过枚举对角顶点完成分割
注意:这里的坐标是计算机中数组位置坐标,可不是数学中的坐标!!数据位置的坐标,描述的是一个方格子,数学坐标描述的是一个点!下面的推导如果按数学来理解就理解不了了!
如下图所示:
竖着切:
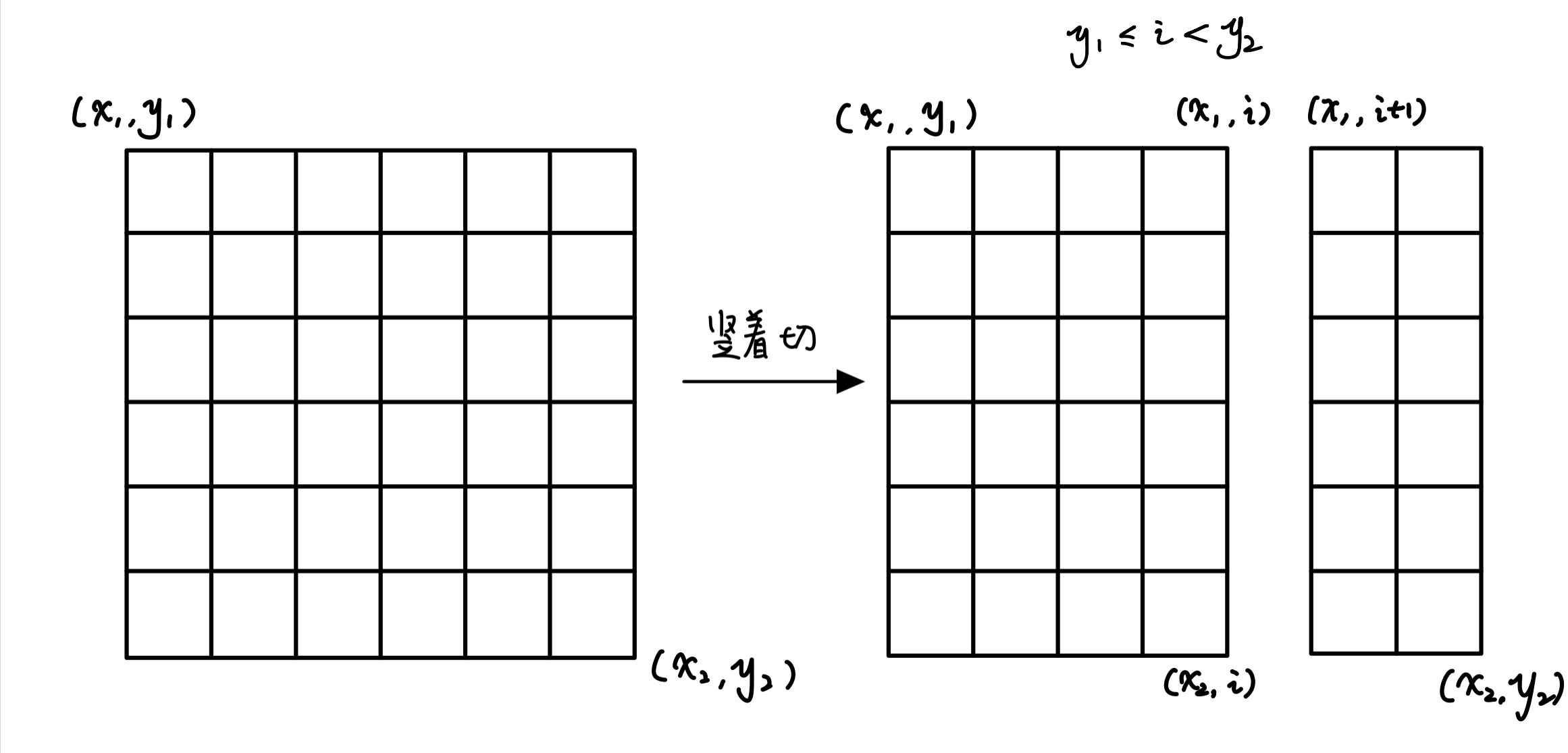
横着切:
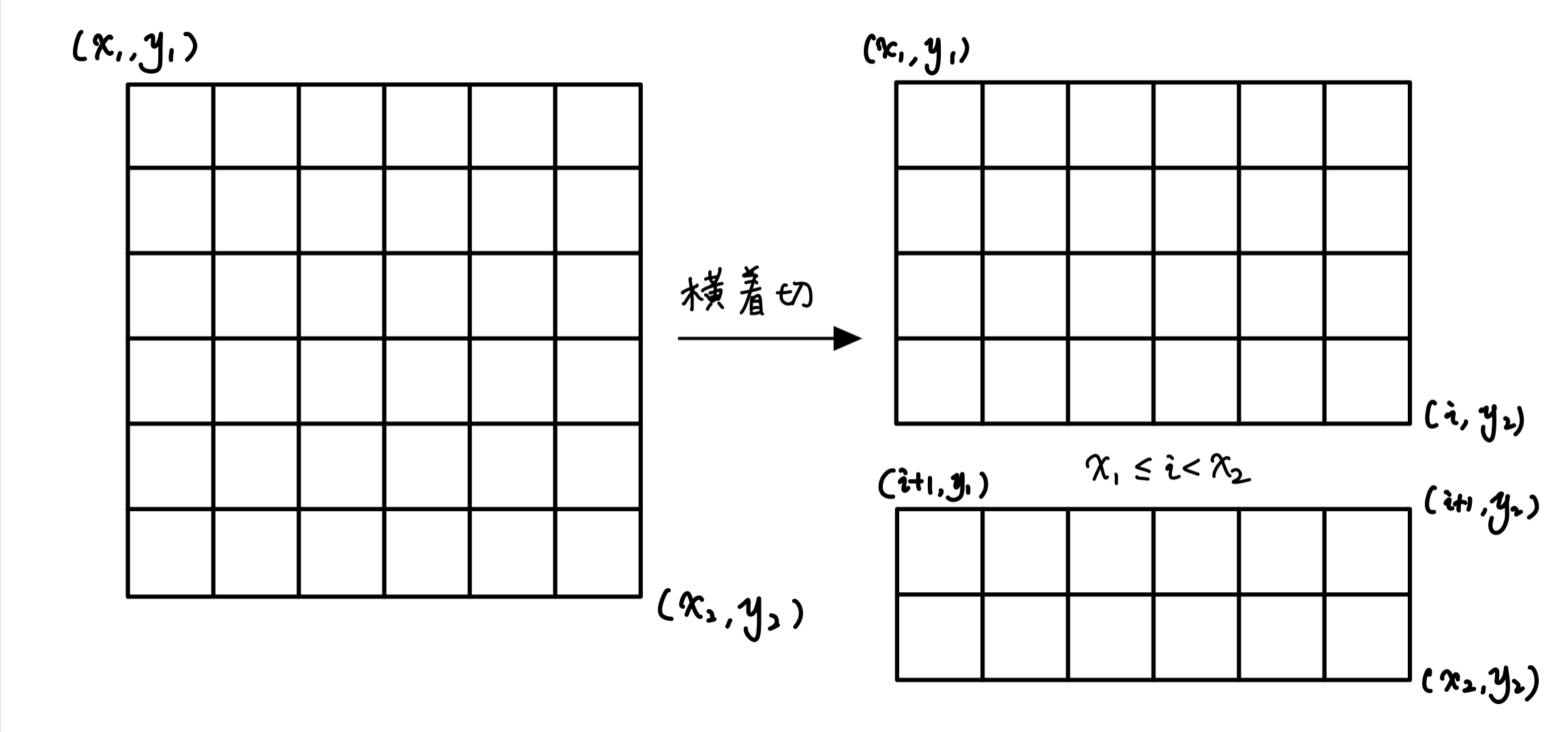
三、记忆化搜索代码实现
#include <bits/stdc++.h>
using namespace std;
const int N = 10; //8*8个格子,我们从下标1开始放入,需要用到下标8,开9个。
int n;
int m = 8;
int s[N][N]; //二维前缀和
double f[N][N][N][N][N]; //DP结果数组
double X; //平均值
//二维前缀和应用
int get_sum(int x1, int y1, int x2, int y2) {
return s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1];
}
//均方差公式[就是模拟了一下题目给的公式]
double get(int x1, int y1, int x2, int y2) {
double sum = get_sum(x1, y1, x2, y2) - X;
return sum * sum / n;
}
/**
* 功能:记忆化搜索
* @param x1 左上角x坐标
* @param y1 左上角y坐标
* @param x2 右下角x坐标
* @param y2 右下角y坐标
* @param k 剩余的刀数
* @return 根据公式计算出的最小值
*/
double dfs(int x1, int y1, int x2, int y2, int k) {
//用一个v来简写一下,要不太长了
double &v = f[x1][y1][x2][y2][k];//这个引用方法很棒,get到了一个知识点
if (v >= 0) return v; //计算过了,就直接返回,不再重复计算
if (k == 0) return v = get(x1, y1, x2, y2);//如果k=0,表示刀都用完了,最终这一块可以计算出来了
//v:-1 表示没有计算过 v:INT_MAX 马上要进行计算,先设置最大
v = INT_MAX;
//每次枚举的是i和i + 1之间的分界线。
//选择横着切,从x1行开始(这个是固定的),到i行(需要枚举的)结束
for (int i = x1; i < x2; i++) {
//放弃上半部分,选择下半部分
v = min(v, get(x1, y1, i, y2) + dfs(i + 1, y1, x2, y2, k - 1));
//放弃下半部分,选择上半部分
v = min(v, get(i + 1, y1, x2, y2) + dfs(x1, y1, i, y2, k - 1));
}
//选择纵着切
for (int i = y1; i < y2; i++) {
//放弃左半部分,选择右半部分
v = min(v, get(x1, y1, x2, i) + dfs(x1, i + 1, x2, y2, k - 1));
//放弃右半部分,选择左半部分
v = min(v, get(x1, i + 1, x2, y2) + dfs(x1, y1, x2, i, k - 1));
}
//返回打擂台的最小值
return v;
}
int main() {
cin >> n;
for (int i = 1; i <= m; i++)
for (int j = 1; j <= m; j++) {
//原数组不用保存,直接用一个二维前缀和数组s即可
cin >> s[i][j];
//二维前缀和构建
s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
}
//利用二维前缀和的结果,计算出平均值,注意要使用double的类型转换,防止丢失精度
X = (double) s[m][m] / n;
//将DP数组初始化为负无穷,计算过的>=0 (因为均方差可能为0),未计算过的为-INF
//方便获取哪个位置是否计算过
memset(f, -1, sizeof f);
//记忆化搜索:因为最后需要切出n块矩形棋盘,其实就是需要切n-1刀,开始dfs模拟
printf("%.3lf\n", sqrt(dfs(1, 1, 8, 8, n - 1)));
return 0;
}
在枚举到的每个场景下,依然可以采用继续横切或竖切的方法,这样就做到了不遗漏任何一种场景,但会有大量的重复计算,采用记忆化可以解决重复计算的问题。