一、知识架构
(1) (01)背包
(N)个物品,容量(V)的背包(上限),(w_i)表示物品的体积,(v_i)表示价值
如何组装背包,在(V)的上限限制情况下,使得价值最大,求最大值。
总结:每个物品只有(1)个,可以选或不选,求在容量限制下的价值最大值。
(2) 完全背包
每个物品有无限个,求价值最大是多少。
(3) 多重背包
每个物品个数不一样,不是无限,也不是只有一个,有(k_i)的个数限制。
多重背包有一个二进制优化的扩展,称为“多重背包II”,就是打包策略。
(4) 分组背包
物品有(n)组,各一组有若干个。每一组最多选择一个物品,比如水果组选择了苹果,就不能选香蕉。
注意:不一定要装满背包
二、01背包的递归表示法

#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int n; //物品的数量
int m; //背包的体积上限
int w[N]; //每个物品的价值
int v[N]; //每个物品的体积
/**
* 功能:深度优先搜索+记忆化解决01背包
* @param step 走到第step物品面前
* @param r 剩余容量r
* @return 可以获得的最大价值是多少
*/
int dfs(int step, int r) {
//如果都出界了,返回0
if (step == n + 1) return 0;
//结果
int res;
//如果不够装下,只能放弃
if (v[step] > r) res = dfs(step + 1, r);
//如果可以装下,可以选择要、还是不要
else res = max(dfs(step + 1, r), dfs(step + 1, r - v[step]) + w[step]);
return res;
}
int main() {
//优化输入
ios::sync_with_stdio(false);
//物品个数与背包容量
cin >> n >> m;
//读入每个物品的体积和价值
for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];
//深搜并输出结果~
cout << dfs(1, m) << endl;
return 0;
}
递归表示法的缺点:
因为有大量的重复计算,所以,不出意外的在大数据量的情况下,(TLE)了!我们需要找一个办法进行优化。
三、记忆化搜索
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int n; //物品的数量
int m; //背包的容量上限
int w[N]; //每个物品的重量(价值)
int v[N]; //每个物品的体积
int dp[N][N]; //引入dp数组保存已经计算过的结果
/**
* 功能:深度优先搜索+记忆化解决01背包
* @param step 走到第step物品面前
* @param r 剩余容量r
* @return 可以获得的最大价值是多少
*/
int dfs(int step, int r) {
//判断这种情况是否被计算过
if (dp[step][r] > 0) return dp[step][r];
//如果都出界了,返回0
if (step == n + 1) return 0;
//结果
int res;
//如果不够装下,只能放弃
if (v[step] > r) res = dfs(step + 1, r);
//如果可以装下,可以选择要、还是不要
else res = max(dfs(step + 1, r), dfs(step + 1, r - v[step]) + w[step]);
//保存结果
dp[step][r] = res;
return res;
}
int main() {
//优化输入
ios::sync_with_stdio(false);
//物品个数与背包容量
cin >> n >> m;
//读入每个物品的体积和价值
for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];
//深搜并输出结果
cout << dfs(1, m) << endl;
return 0;
}
四、二维数组法
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main() {
//优化输入
ios::sync_with_stdio(false);
//物品个数n
cin >> n >> m;
//读入体积和重量
for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) {
if (j >= v[i]) f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]); //两种情况取最大值
else f[i][j] = f[i - 1][j];
}
cout << f[n][m] << endl;
return 0;
}
五、一维数组法
为什么要用一维数组优化01背包问题
因为我们看到上面的存储方式,其实第(i)件物品选择或不选择两种方式,都只和(i-1)时的情况相关联,也就是说在(i-1)再以前的状态和数据与(i)无关,换句话说,就是没啥用了,可以清除掉了。这样一路走一路依赖它前面一行就OK,可以把二维数组优化为一维。
那么,怎么个优化法呢?答案是用一个一维数组。
这里最核心的问题是为什么容量的遍历要从大到小,和上面二维的不一样了呢??
这是因为第(i)个要依赖于第(i-1)个,如果从小到大,那么(i-1)先变化了,而(i)说的依赖于(i-1),其实是在没变化前的(i-1) 信息,这么直接来就错了。那怎么才能对呢?就是从大到小反向遍历,这样(i-1)都是以前的信息,还没变,就OK了!有点绕啊,但还算好理解!
#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main() {
//优化输入
ios::sync_with_stdio(false);
//物品个数n
cin >> n >> m;
//读入体积和重量
for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];
//01背包模板
for (int i = 1; i <= n; i++)
for (int j = m; j >= v[i]; j--)
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
return 0;
}
六、01背包之恰好装满【一般不考】
恰好装满:
求最大值时,除了(dp[0]) 为0,其他都初始化为无穷小 -0x3f3f3f3f
求最小值时,除了(dp[0]) 为0,其他都初始化为无穷大 0x3f3f3f3f
不必恰好装满: 全初始化为0
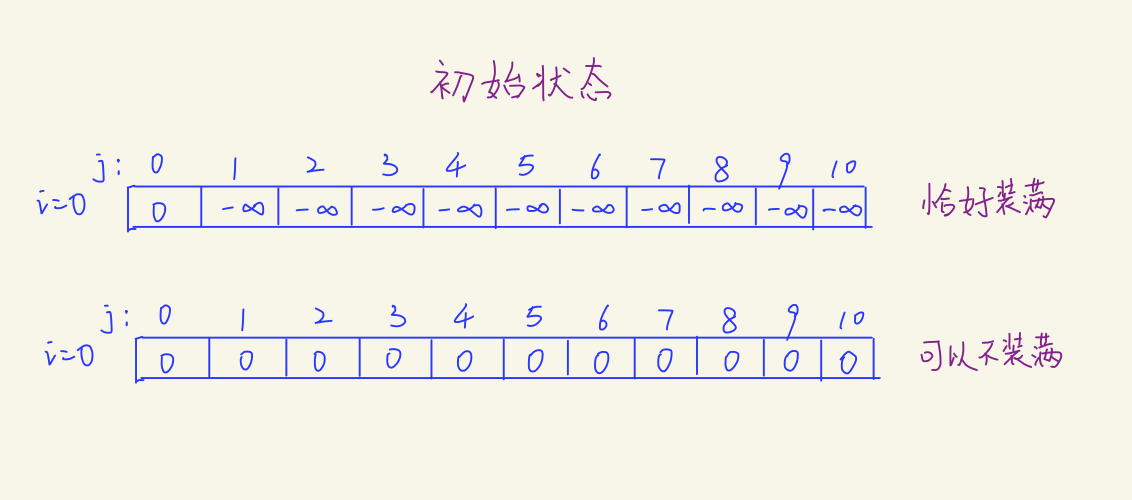
为什么呢?因为初始化的数组,实际上是在没有任何物品可以放入背包的情况下的合法状态。如果要求背包恰好装满,那么此时只有容量为0的背包可以在什么都不装且价值为0的情况下被“恰好装满”,其他容量的背包均没有合法的解,因此属于未定义的状态,应该设置为负无穷大。如果背包不需要被装满,那么任何容量的背包都有合法解,那就是“什么都不装”。这个解的价值为0,所以初始状态的值都是0。
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main() {
//物品个数n
cin >> n >> m; //m:背包容积,就是大V
//初始化f[0]=0,其它设置负无穷
memset(f,-0x3f,sizeof f);
f[0]=0;
//读入体积和重量
for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];
for (int i = 1; i <= n; i++)
for (int j = m; j >=v[i]; j--) {
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
cout << f[m] << endl;
return 0;
}