AcWing 858. Prim算法求最小生成树

一、最小生成树

1、知识框架图

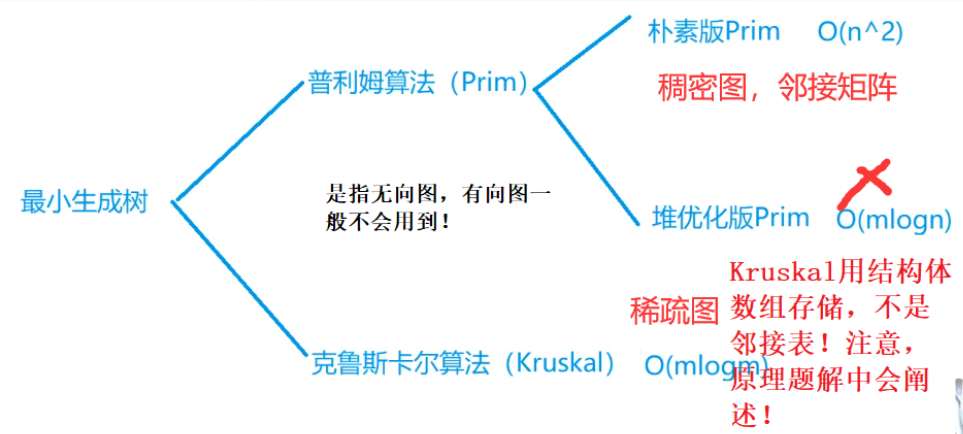
2、最小生成树概念

最小生成树一般是说的无向图，有向图的最小生成树一般不会用到。
连通图：在无向图中，若任意两个顶点(v_i)与(v_j)都有路径相通，则称该无向图为连通图。
连通网：在连通图中，若图的边具有一定的意义，每一条边都对应着一个数，称为权；权代表着连接连个顶点的代价，称这种连通图叫做连通网。
生成树：一个连通图的生成树是指一个连通子图，它含有图中全部(n)个顶点，但只有足以构成一棵树的(n-1)条边。一颗有(n)个顶点的生成树有且仅有(n-1)条边，如果生成树中再添加一条边，则必定成环。
最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。一个无向图可以有多个最小生成树，但最小生成树的边权和一定是最小的。

实际的场景：
比如(N)个城市，需要根据实际情况建高铁，我们知道这些城市之间有些是相通的，距离也知道，有些城市之间是不通的，也不打算建高铁。那么，我们如何能知道怎么建设高铁的路线使用城市之间全能连通，并且路线和最小呢？因为这样才省钱，还能保证所有城市联通啊！

二、Prim算法

和(dijkstra)非常相似,(dijkstra)算法是计算到顶点的距离，而(Prim)算法是计算到集合的距离，下面详细讲解：

比如本题:稠密图，节点个数(500),边数(10^5),好多的边啊，所以需要定义(g[N][N]), $500*500=250000 > 10^5 $。

prim 算法采用的是一种贪心的策略,每次将离连通部分的最近的点和点对应的边加入的连通部分，连通部分逐渐扩大，最后将整个图连通起来，并且边长之和最小。

算法步骤

把所有距离dist[N]初始化为INF。
用一个 pre 数组保存节点的是和谁连通的。pre[i] = k 表示节点 i 和节点 k 之间需要有一条边。初始时，pre 的各个元素置为 -1。
循环n次，将所有点准备加入到集合中。
（1）.找出不在集合中的(!st[j])距离集合最近的点'dist[j]'，如果是有多个距离一样近，那么选择号小的那个,命名为t。
（2）.累加最小权值
（3）.利用t更新未加入集合中的其它各点到集合的最短距离。
（4）.将t加入到集合中。

模拟流程

我们将图中各个节点用数字 (1 sim n) 编号。

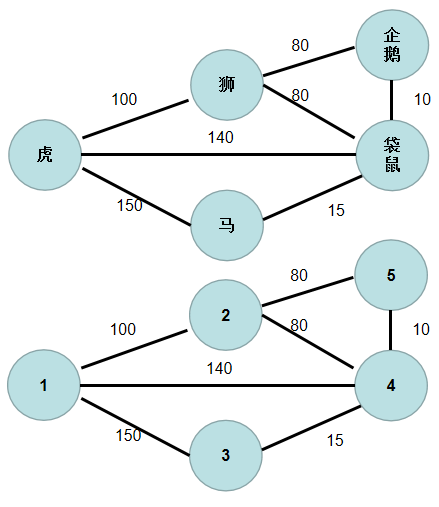
要将所有景点连通起来，并且边长之和最小，步骤如下：
用一个 (st) 数组表示节点是否已经连通。(st[i]) 为真，表示已经连通，(st[i]) 为假，表示还没有连通。初始时，(st) 各个元素为假。即所有点还没有连通。
用一个 (dist) 数组保存各个点到连通部分的最短距离，(dist[i]) 表示 (i) 节点到连通部分的最短距离。初始时，(dist) 数组的各个元素为无穷大。
用一个 (pre) 数组保存节点的是和谁连通的。(pre[i] = k) 表示节点 (i) 和节点 (k) 之间需要有一条边。初始时，(pre) 的各个元素置为 (-1)。
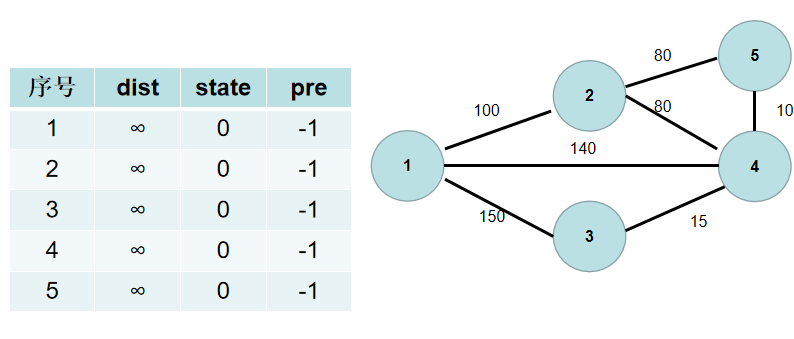
从 (1) 号节点开始扩充连通的部分，[之所以从一号结点开始，是因为大家都是距离集合正无穷，那么号小的优化！]，所以 (1) 号节点与连通部分的最短距离为 (0)，即(dist[i]) 值为 0。
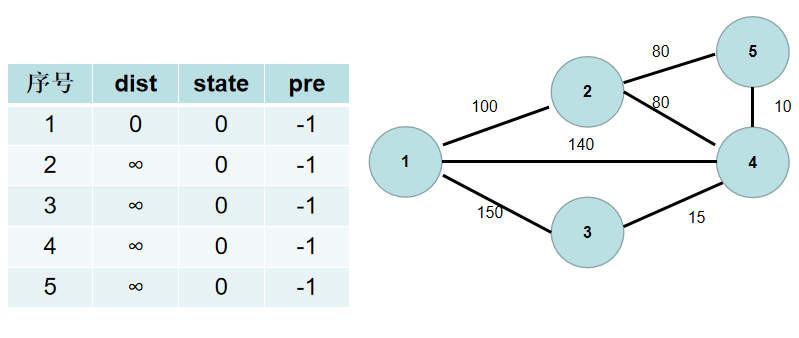
遍历 (dist) 数组，找到一个还没有连通起来，但是距离连通部分最近的点，假设该节点的编号是 (t)。(t)节点就是下一个应该加入连通部分的节点，(st[t]) 置为 (true)。
用青色点表示还没有连通起来的点，红色点表示连通起来的点。这里青色点中距离最小的是 (dist[1])，因此 (st[1]) 置为 (true)。

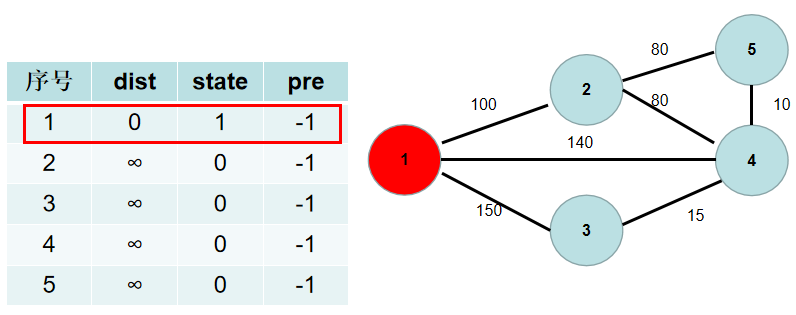
4.遍历所有与 (t) 相连但没有加入到连通部分的点 (j)，如果 (j) 距离连通部分的距离大于 (t sim j) 之间的距离，即 (dist[j] > g[t][j])（(g[t][j]) 为 (t sim j) 节点之间的距离），则更新 (dist[j]) 为 (g[t][j])。这时候表示，(j) 到连通部分的最短方式是和 (t) 相连，因此，更新(pre[j] = t)。

与节点 (1) 相连的有 (2)， (3)， (4) 号节点。(1->2) 的距离为 (100)，小于 (dist[2])，(dist[2]) 更新为 (100)，(pre[2]) 更新为(1)。(1->4) 的距离为 (140)，小于 (dist[4])，$dist[4] $更新为 (140)，(pre[4]) 更新为(1)。(1->3) 的距离为 (150)，小于 (dist[3])，(dist[3]) 更新为 (150)，(pre[3]) 更新为(1)。

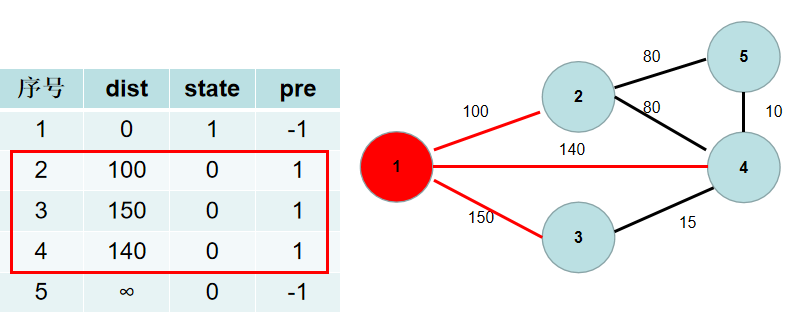
重复 (3), (4)步骤，直到所有节点的状态都被置为 (1).
这里青色点中距离最小的是 (dist[2])，因此 (st[2]) 置为 (1)。

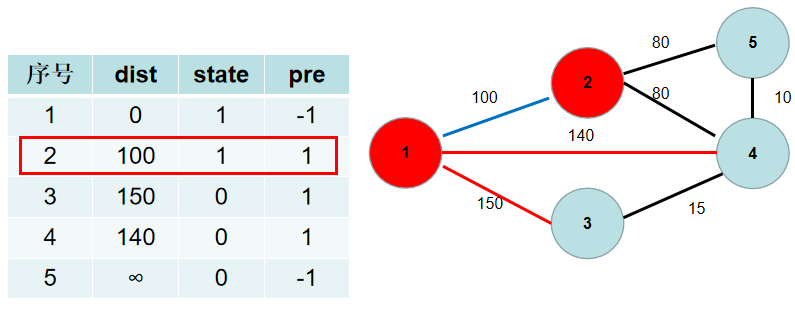
与节点 (2) 相连的有 (5)， (4)号节点。(2->5) 的距离为 (80)，小于 (dist[5])，(dist[5]) 更新为 (80)，(pre[5]) 更新为 (2)。(2->4) 的距离为 (80)，小于 (dist[4])，(dist[4]) 更新为 (80)，(pre[4]) 更新为(2)。

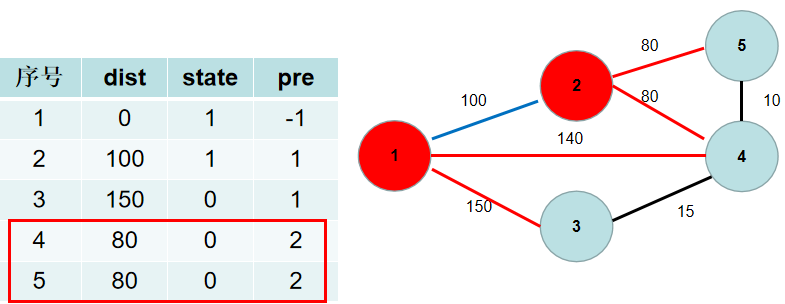
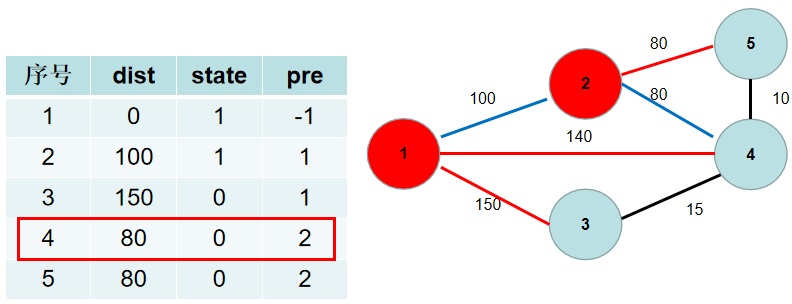
选(dist[4])，更新(dist[3])，(dist[5])，(pre[3])，(pre[5])。

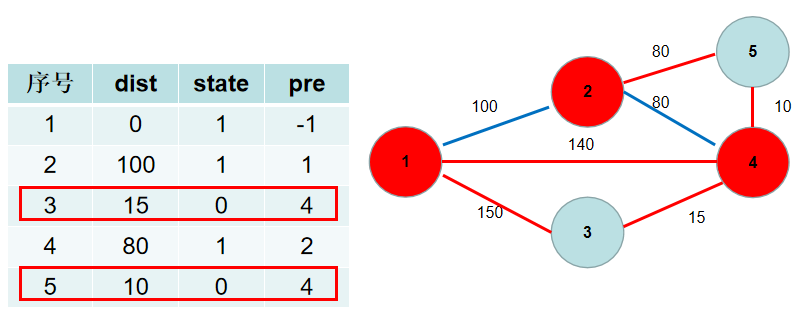
选(dist[5])，没有可更新的。

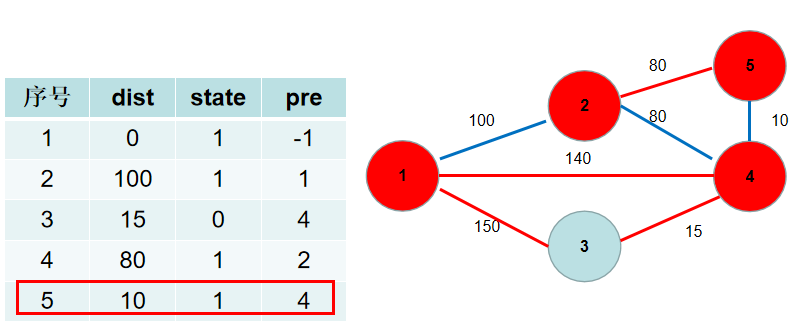
选(dist[3])，没有可更新的。

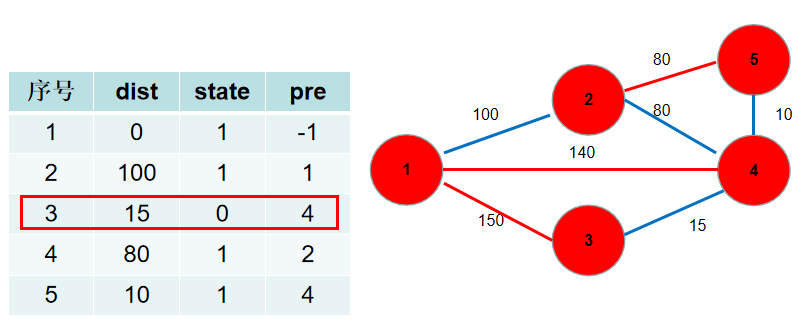
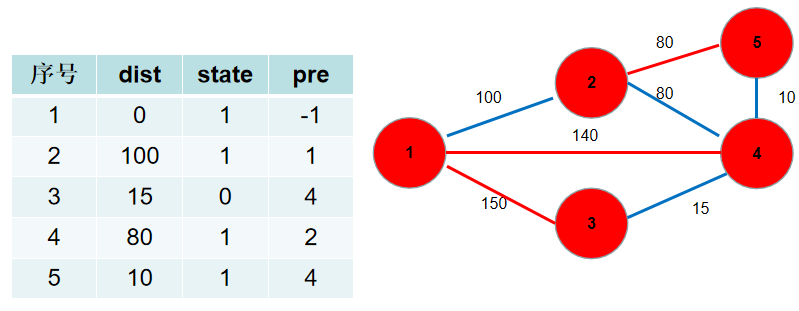
6.此时 (dist) 数组中保存了各个节点需要修的路长，加起来就是。(pre) 数组中保存了需要选择的边。

经验总结

最小生成树并不唯一，但它的边权最小值是唯一的。所以，一般没有要求求出最小生成树长成什么样子，而是要求输出最小生成树的边权最小值。
因为(Prim)算法需要反复的求每两个点之间的距离，这就决定了邻接矩阵更合适，因为相对于邻接表，邻接矩阵可以快速提供两个点之间的距离，而邻接表是链表，想要获取两个点之间的距离就没那么方便。
边数较少可以用(Kruskal),因为(Kruskal)算法每次查找最短的边。边数较多可以用(Prim)，因为它是每次加一个顶点，对边数多的适用。
堆优化的(Prim)算法一般不用。
图论的题一般难就难在建图上，考虑算法原理的并不多啊，所以理解并背下来算法模板的思路就非常重要了，主要是用自然语言复述，不要死记硬背模板代码，那样容易忘，也记不住。

三、朴素版Prim算法代码

#include <bits/stdc++.h>

using namespace std;
const int N = 510;
const int INF = 0x3f3f3f3f;

int n, m;
int g[N][N];    //稠密图，邻接矩阵
int dist[N];    //这个点到集合的距离
bool st[N];     //是不是已经使用过
int res;        //最小生成树里面边的长度之和

/**
 * 功能：普利姆算法求最小生成树
 * @return
 */
int prim() {
    //迭代n次
    for (int i = 0; i < n; i++) {
        //1、找到集合外，距离集合最近的点
        int t = -1;
        for (int j = 1; j <= n; j++)
            if (!st[j] && (t == -1 || dist[t] > dist[j])) t = j;
        /*如果不是第一个点，并且距离是INF，说明现在没有点可以连通到生成树，
         这时不是连通图，没有最小生成树，返回INF*/
        if (i && dist[t] == INF) return INF;
        /*是第一个结点，dist[1]应该是0,现在初始化的是INF,所有这里特判一下。
        不是第一个点,结果加上这条边的权值。*/
        if (i)res += dist[t];
        //2、因为本轮选择的是结点t,那么用t更新其它未加入到集合中点到集合的距离
        for (int j = 1; j <= n; j++) dist[j] = min(dist[j], g[t][j]);
        //3、把t放到集合中
        st[t] = true;
    }
    return res;
}

int main() {
    //读入优化
    ios::sync_with_stdio(false);
    cin >> n >> m;
    //所有点之间的距离初始化为正无穷，然后再读入所有边
    memset(g, 0x3f, sizeof g);
    //距离初始化无穷大,表示所有结点都在生成树之外
    memset(dist, 0x3f, sizeof dist);
    //读入数据
    while (m--) {
        int a, b, c;
        cin >> a >> b >> c;
        g[a][b] = g[b][a] = min(g[a][b], c);
        //允许重复，构建双向有向成为无向图,同时保留最小的
    }
    int t = prim();//普利姆算法
    //输出结果
    if (t == INF) puts("impossible");
    //不存在生成树，比如所有点不连通的情况下
    else printf("%d
", t); //否则输出t

    return 0;
}

四、带路径输出的Prim算法

#include <bits/stdc++.h>

using namespace std;
const int N = 510;
const int INF = 0x3f3f3f3f;

int n, m;
int g[N][N];    //稠密图，邻接矩阵
int dist[N];    //这个点到集合的距离
bool st[N];     //是不是已经使用过
int res;        //最小生成树里面边的长度之和
int pre[N];     //前驱结点

/**
 * 功能：普利姆算法求最小生成树
 * @return
 */
int prim() {
    //迭代n次
    for (int i = 0; i < n; i++) {
        int t = -1;
        for (int j = 1; j <= n; j++)
            if (!st[j] && (t == -1 || dist[t] > dist[j])) t = j;
        if (i && dist[t] == INF) return INF;
        if (i)res += dist[t];
        for (int j = 1; j <= n; j++)
            if (!st[j]) {
                if (g[t][j] < dist[j]) {
                    dist[j] = g[t][j];
                    pre[j] = t;
                }
            }
        st[t] = true;
    }
    return res;
}


int main() {
    //读入优化
    ios::sync_with_stdio(false);
    cin >> n >> m;
    memset(g, 0x3f, sizeof g);
    memset(dist, 0x3f, sizeof dist);
    memset(pre, -1, sizeof pre);
    //读入数据
    while (m--) {
        int a, b, c;
        cin >> a >> b >> c;
        g[a][b] = g[b][a] = min(g[a][b], c);
    }
    int t = prim();
    if (t == INF) puts("impossible");
    else printf("%d
", t);

    //输出前驱结点
    for (int i = 1; i <= n; i++)
        printf("%d ", pre[i]);
    return 0;
}