一、历史背景
1736年,年仅29岁的数学家欧拉来到普鲁士的古城哥尼斯堡(哲学家康德的故乡,今俄罗斯加里宁格勒)。普瑞格尔河正好从市中心流过,河中心有两座小岛,岛和两岸之间建筑有七座古桥。
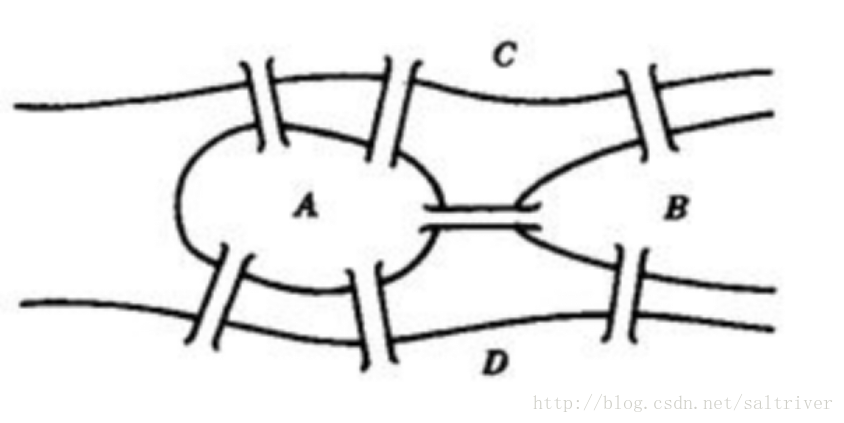
欧拉发现当地居民有一项消遣活动,就是试图每座桥恰好走过一遍并回到原出发点,但从来没人成功过。
欧拉证明了这种走法是不可能的。现在看来,欧拉的证明过程非常简单,但他对七桥问题的抽象和论证思想,开创了一个新的学科:图论(Graph)。
如今,无论是数学、物理、化学、天文、地理、生物等基础科学,还是信息、交通、经济乃至社会科学的众多问题,都可以应用图论方法予以解决。图论还是计算机科学的数据结构和算法中最重要的框架(没有之一)。
首先能想到的证明方法是把走七座桥的走法都列出来,一个一个的试验,但七座桥的所有走法共用(7!=5040种),逐一试验将是很大的工作量。欧拉作为数学家,当然没那样想。欧拉把两座岛和河两岸抽象成顶点,每一座桥抽象成连接顶点的一条边,那么哥尼斯堡的七座桥就抽象成下面的图:
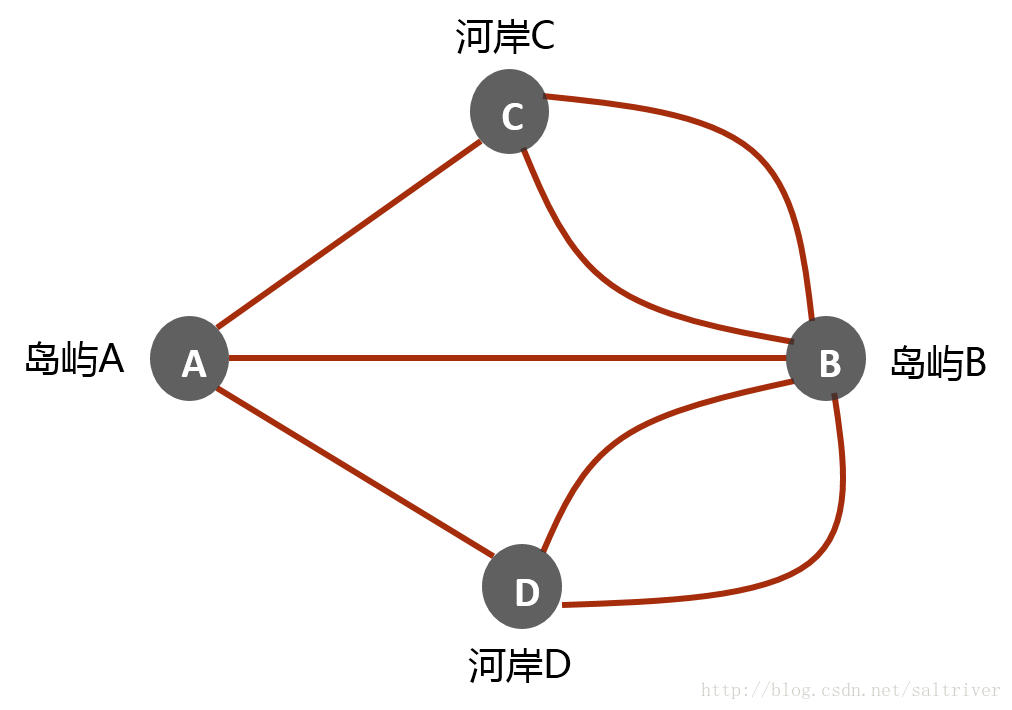
假设每座桥都恰好走过一次,那么对于(A、B、C、D)四个顶点中的每一个顶点,需要从某条边进入,同时从另一条边离开。进入和离开顶点的次数是相同的,即每个顶点有多少条进入的边,就有多少条出去的边,也就是说,每个顶点相连的边是成对出现的,即每个顶点的相连边的数量必须是偶数。
而上图中(A、C、D)四个顶点的相连边都是3,顶点(B)的相连边为5,都为奇数。因此,这个图无法从一个顶点出发,遍历每条边各一次。
欧拉的证明与其说是数学证明,还不如看作是一个逻辑证明。一个曾难住那么多人的问题,竟然是这样一个简单的出人意料的推理,还开创了一个新的学科。欧拉非常巧妙的把一个实际问题抽象成一个合适的数学模型,这种研究方法就是我们应该掌握的数学模型方法。这并不需要运用多么深奥的理论,但能想到这一点,却是解决问题的关键。
二、相关的概念和定理
欧拉图、欧拉路径/回路
- 如果在一张图(有向图或无向图)上能够不重复地遍历完所有的边,那么此图就称为欧拉图(Eulerian graph)。
- 能够不重复地遍历完所有的边的路径——即一笔画的“笔画”,称为欧拉路径(Eulerian path)。
- 特别地,如果上述路径的起点与终点相同,则称为欧拉回路(Eulerian circuit)。
如下gif所示的图就是欧拉图,存在一个欧拉路径。

下图是一笔画成的“串”字,也就是说烧烤店门口挂的这个字可以用单条LED灯带做成。

那么柯尼斯堡七桥问题为什么不能“一笔画”呢?来看看欧拉提出的定理。
图论中的欧拉定理(一笔画定理)
欧拉同时考虑到了有向图与无向图的情况,因此要分别讨论。
无向图的情况
定理:
连通无向图G有欧拉路径的充要条件为:G中奇度顶点(即与其相连的边数目为奇数的顶点)有0个或者2个。
证明:
略,NOIP级别的竞赛,不考证明,知道结论就行了。
可知,柯尼斯堡七桥问题中的图有(4个)奇度顶点((1)个度数为(5),(3)个度数为(3)),所以不存在欧拉路径。
有向图的情况
定理:
底图连通的有向图G有欧拉路径的充要条件为:
1、G的所有顶点入度和出度都相等;
2、或者只有两个顶点的入度和出度不相等,且其中一个顶点的出度与入度之差为1,另一个顶点的入度与出度之差为1。
证明略。
欧拉定理介绍完了,那么如何找到具体的路径呢?
寻找欧拉路径/回路
-
判断图的连通性,非连通图是不存在欧拉路径/回路的。
判断图的连通性可以通过传统的DFS和BFS方法,也可以通过之前讲过的并查集实现,另外还有基于传递闭包的Floyd-Warshall算法(没错就是求最短路的那个),不再赘述。
图的连通性判断链接 -
判断是否欧拉路径/回路
如果图是连通的,我们再遍历每个顶点的度(有向图就是入度和出度),根据欧拉定理即可轻松地判断图中是否欧拉路径/回路。 -
找出路径的起点和终点
如果是欧拉路径的话,还能顺便找出路径的起点和终点。
#include <bits/stdc++.h>
using namespace std;
const int N = 26;
int ind[N]; //入度
/**
测试数据:
欧拉图
4 4
1 2
2 3
3 4
4 1
非欧拉图
4 4
1 2
2 3
3 4
1 4
*/
struct Edge { //记录边的终点,边权的结构体
int to; //终点
int value; //边权
};
int n, m; //表示图中有n个点,m条边
vector<Edge> p[N]; //使用vector的邻接表
int cnt, start;
int main() {
//利用邻接表建图
cin >> n >> m;
//m条边
for (int i = 1; i <= m; i++) {
int u, v; //点u到点v有一条权值为l的边
cin >> u >> v;
p[u].push_back({v, 1});
//维护入度
ind[v]++;
}
//判断是不是欧拉图
//出度与入度的数字关系
for (int i = 1; i <= n; i++) {
//计算每个结点的出度与入度的差
int k = p[i].size() - ind[i]; //出度不需要单独维护
//出度与入度差大于1,则肯定不是欧拉图
if (abs(k) > 1) {
cout << "No";
return 0;
}
//如果差是1,那么需要检查是不是2个,2个才是一个入口点,一个出口点
if (abs(k) == 1) {
//记录个数
cnt++;
//如果出度比入度大1,记录下起点是哪个结点
if (k == 1) start = i;
}
}
//如果不是0也不是2,那么不是欧拉图
if (cnt != 0 && cnt != 2) {
cout << "No";
return 0;
}
//欧拉图
cout << "Yes" << endl;
if (start) cout << "出发点:" << start << endl;
else cout << "任意点都可以是出发点!" << endl;
return 0;
}