主要填补知识漏洞:
一、母函数分析法
(1)普通母函数
在考虑“当投掷n粒骰子时,加起来点数总和等于m的可能方式的数目”这个问题时首先使用了母函数方法,并得出可能的数目是 的展开式中
的展开式中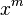 项的系数。
项的系数。
典型模型:砝码称重
特点:求某个解权重之和的解数
例题:有1,2,3g的砝码各一个,称出质量为3的砝码,有几种组合方法。
G(x)=(1+x)(1+x^2)(1+x^3) 答案是x^3的系数。因为幂函数相乘指数相加。
拓展:若是3种砝码有无数种
G(x)=(1+x+x^2+x^3+x^4....)(1+x^2+x^4+x^6....)(1+x^3+x^6+x^9...) 同样 答案是x^3的系数。
例题:HDU2082 http://acm.hdu.edu.cn/showproblem.php?pid=2082
AC代码:

1 /*HDU2082 2 普通型母函数 3 题目:假设有x1个字母A, x2个字母B,..... x26个字母Z,同时假设字母A的价值为1,字母B的价值为2,..... 字母Z的价值为26。那么,对于给定的字母,可以找到多少价值<=50的单词呢? 4 G(x)=(1+x+x^2+x^3...x^x1)(1+x^2+x^4+...x^(x2^2))(1+x^3....) 5 答案就是G(x)展开后的指数小于等于50的项的常数系数之和 6 */ 7 #include <cmath> 8 #include <algorithm> 9 #include <stdlib.h> 10 #include <iostream> 11 #include <string.h> 12 #include <stdio.h> 13 #include <stack> 14 #include <set> 15 #include <map> 16 #include <vector> 17 #define LL long long 18 #define maxn 77 19 using namespace std; 20 LL T; 21 LL a[maxn],b[maxn]; 22 23 int main(){ 24 cin>>T; 25 while(T--){ 26 memset(a,0,sizeof(a)); 27 memset(b,0,sizeof(b)); 28 a[0]=1; 29 for(int i=1;i<=26;i++){ 30 int t; 31 cin>>t; 32 if (t==0) continue; 33 for(int j=0;j<=50;j++){ 34 for(int k=0;k+j<=50 && k<=t*i;k+=i){ 35 b[j+k]+=a[j]*1; 36 } 37 } 38 for(int i=0;i<=50;i++) a[i]=b[i]; 39 memset(b,0,sizeof(b)); 40 } 41 LL ans=0; 42 for(int i=1;i<=50;i++) ans+=a[i];//注意x的下限 43 cout<<ans<<endl; 44 } 45 return 0; 46 }
(2)整数的拆分
描述:将N拆分成多个正整数的和,注意拆分的数和顺序无关。例4=1+3和4=3+1是等效的。
母函数的应用:
考虑上下限,N最多使用一张N的权值的牌。所以可以在有限的范围内通过G(x)计算出来
G(x)=(1+x+x^2+x^3+...x^N)(1+x^2+x^4...x^(N/2*2))(1+x^3+x^6....).....(1+x^N)
最后解就是x^N项的系数。注意:由母函数指数运算的性质,在计算指数的时候可以优化掉超出N指数范围的项。
例题:HDU1028
AC代码:

1 /*HDU1028 2 正整数的拆分(母函数的应用) 3 题目:将N这个正整数(1<=N<=120)拆分方法有哪些? 4 例如: 5 4 = 4; 6 4 = 3 + 1; 7 4 = 2 + 2; 8 4 = 2 + 1 + 1; 9 4 = 1 + 1 + 1 + 1; 10 f(4)=5 11 分析: 考虑上下限,N最多使用一张N的权值的牌。所以可以在有限的范围内通过G(x)计算出来 12 13 G(x)=(1+x+x^2+x^3+...x^N)(1+x^2+x^4...x^(N/2*2))(1+x^3+x^6....).....(1+x^N) 14 15 最后解就是x^N项的系数。注意:由母函数指数运算的性质,在计算指数的时候可以优化掉超出N指数范围的项。 16 */ 17 #include <cmath> 18 #include <algorithm> 19 #include <stdlib.h> 20 #include <iostream> 21 #include <string.h> 22 #include <stdio.h> 23 #include <stack> 24 #include <set> 25 #include <map> 26 #include <vector> 27 #define LL long long 28 #define maxn 155 29 using namespace std; 30 LL N; 31 LL a[maxn],b[maxn]; 32 //G(x)=(1+x+x^2+x^3+...x^N)(1+x^2+x^4...x^(N/2*2))(1+x^3+x^6....).....(1+x^N) 33 int main(){ 34 while(cin>>N){ 35 memset(a,0,sizeof(a)); 36 memset(b,0,sizeof(b)); 37 a[0]=1; 38 for(int i=1;i<=N;i++){//枚举步长(即“牌”的权值) 39 for(int j=0;j<=N;j++){//枚举计算到上一步已有的项 40 for(int k=0;j+k<=N;k+=i){//枚举新的项(下一个括号),注意这道题中系数都是1 41 b[j+k]+=a[j]; 42 } 43 } 44 for(int i=0;i<=N;i++) a[i]=b[i]; 45 memset(b,0,sizeof(b)); 46 } 47 LL ans=a[N]; 48 cout<<ans<<endl; 49 } 50 return 0; 51 }
(3)Ferrers图像
描述:一个从上而下的n层格子,mi 为第i层的格子数,当mi>=mi+1(i=1,2,,n-1) ,即上层的格子数不少于下层的格子数时,称之为Ferrers图像。
性质:(1)每一层至少有一个格子;
(2)第一行与第一列互换,第二行与第二列互换,…,所得到的图象仍然是Ferrers图象,这两个 Ferrers图象称为是一对共轭的Ferrers图象。
(3)或者说是这样:以从左上到右下的斜线为对称轴,将图片翻转一下
应用:由Ferrers图像可以得到关于整数拆分的一些性质
(1)正整数n拆分成k个数的和的拆分数=n拆分成最大数为k的拆分数
(2)正整数n拆分成最多不超过k个数的拆分数=n拆分成最大不超过k的拆分数(注意和(1)的描述的差别,可由(1)归纳推理得到)
(3)正整数n拆分成不超过k的数的和的拆分数=将n+k拆分成恰好k个数的拆分数
吐槽:这些性质比较难应用吧,不过可以转换思维,进而转换要枚举的对象.
(4)指数型母函数
原型:n个元素组成的多重集,其中a1重复了n1次,a2重复了n2次........ak重复了nk次,若n=n1+n2+n3...+nk,则从n个元素中取出r个排列,求不同的排列数。
例如:2个A,一个B,则排列有“AAB”,"ABA","BAA",即相同的元素内部排序算作一种
分析:如果r=n,则f(n,r)=n!/(n1!*n2!....*nk!)这个是高中的基本的排列组数知识
但是如果要求解的r<n,怎么办呢?
指数型母函数:G(x)=(1+x/1+x^2/2!+x^3/3!....x^n1/n1!)(1+x/1+x^2/2!+....x^n2/n2!)...(1+x/1+x^2/2!+...x^nk/nk!)
答案就是(x^r/r!)前面的系数。
例题:HDU1261(指数型母函数+高精度)
AC代码:

1 /*HDU1261 2 题目描述:一个A和两个B一共可以组成三种字符串:"ABB","BAB","BBA". 3 给定若干字母和它们相应的个数,计算一共可以组成多少个不同的字符串. 4 每组测试数据分两行,第一行为n(1<=n<=26),表示不同字母的个数,第二行为n个数A1,A2,...,An(1<=Ai<=12),表示每种字母的个数.测试数据以n=0为结束. 5 6 分析:典型的指数型母函数的模板题。 7 G(x)=(1+x/1+x^2/2!+x^3/3!....x^A1/A1!)(1+x/1+x^2/2!+....x^A2/A2!)...(1+x/1+x^2/2!+...x^A26/A26!) 8 答案:如果r=n,则f(n,r)=n!/(n1!*n2!....*nk!),这道题目就是用上n张的全排了。 9 */ 10 #include <cmath> 11 #include <algorithm> 12 #include <stdlib.h> 13 #include <iostream> 14 #include <string.h> 15 #include <stdio.h> 16 #include <stack> 17 #include <set> 18 #include <map> 19 #include <vector> 20 #define LL long long 21 #define maxn 1550 22 using namespace std; 23 int N; 24 int gcd(int a,int b){ 25 if (a<b) return gcd(b,a); 26 if (b==0) return a;else return gcd(b,a%b); 27 } 28 struct D{ 29 int dig[maxn];//方向存储,从0到高位相乘 30 int b[maxn]; 31 int cnt; 32 void init(){ 33 for(int i=0;i<maxn-5;i++) dig[i]=0; 34 dig[0]=1; 35 cnt=1; 36 } 37 void multi(int num){//这道题的num最大26 38 memset(b,0,sizeof(b)); 39 int m=cnt; 40 for(int i=0;i<cnt;i++){ 41 int k=num*dig[i]; 42 int t=0; 43 while(k>0){ 44 b[i+t]+=k%10; 45 m=max(cnt,i+t+1); 46 if (b[i+t]>9){ 47 b[i+t+1]+=b[i+t]/10; 48 b[i+t]=b[i+t]%10; 49 m=max(m,i+t+2); 50 } 51 k=k/10; 52 t++; 53 } 54 } 55 cnt=m; 56 for(int i=0;i<cnt;i++) dig[i]=b[i]; 57 } 58 void print(){ 59 // cout<<"cnt="<<cnt<<endl; 60 for(int i=cnt-1;i>=0;i--) 61 cout<<dig[i]; 62 printf(" "); 63 } 64 }Dig; 65 int p[maxn]; 66 int A[30]; 67 //ans=f(n,r)=n!/(n1!*n2!....*nk!) 68 //范围:n(1<=n<=26),(1<=Ai<=12),根据范围,可直接暴力 69 //思路:上下约分,约掉公因数,分母剩下的部分用高精度乘法(除法不会写啊) 70 int main(){ 71 // freopen("out.txt","w",stdout); 72 while(cin>>N && N>0){ 73 int T=0; 74 Dig.init(); 75 for(int i=1;i<=N;i++) { 76 cin>>A[i]; 77 T+=A[i]; 78 } 79 // cout<<"T="<<T<<endl; 80 for(int i=1;i<=T;i++) p[i]=i; 81 for(int i=1;i<=N;i++){ 82 int Ai=A[i]; 83 for(int j=2;j<=Ai;j++){ 84 int nj=j; 85 for(int k=1;k<=T;k++){//约分A[k]和j 86 if (p[k]==1) continue; 87 if (nj==1) break; 88 int g=gcd(p[k],nj); 89 p[k]/=g; 90 nj/=g; 91 } 92 } 93 } 94 for(int i=1;i<=T;i++) Dig.multi(p[i]); 95 Dig.print(); 96 } 97 return 0; 98 }
例题:HDU1521
AC代码:

1 /*HDU1521 2 题目描述:有n种物品,并且知道每种物品的数量。要求从中选出m件物品的排列数。例如有两种物品A,B,并且数量都是1,从中选2件物品,则排列有"AB","BA"两种。 3 每组输入数据有两行,第一行是二个数n,m(1<=m,n<=10),表示物品数,第二行有n个数,分别表示这n件物品的数量。 4 分析:典型的指数型母函数的模板题。 5 G(x)=(1+x/1+x^2/2!+x^3/3!....x^A1/A1!)(1+x/1+x^2/2!+....x^A2/A2!)...(1+x/1+x^2/2!+...x^A26/A26!) 6 答案:x^m/m!前的指数 7 ps:题目的数据范围很小,所以可以不用高精度。 8 和HDU1261的高精度联系起来,可以写一道大数+f(n,m)的题目吧 9 这道题目要用到一个技巧(略微觉得损失精度) 10 系数用double存储,这样在不能整除时,保留(部分)精度 11 分析 12 13 */ 14 #include <cmath> 15 #include <algorithm> 16 #include <stdlib.h> 17 #include <iostream> 18 #include <string.h> 19 #include <stdio.h> 20 #include <stack> 21 #include <set> 22 #include <map> 23 #include <vector> 24 #define LL long long 25 #define maxn 1001 26 using namespace std; 27 int N,M; 28 double a[maxn],b[maxn]; 29 int F[1001],A[1001]; 30 void init(){ 31 F[0]=1; 32 for(int i=1;i<=10;i++){ 33 F[i]=F[i-1]*i; 34 } 35 return; 36 } 37 int main(){ 38 // freopen("out.txt","w",stdout); 39 init(); 40 while(cin>>N>>M){ 41 for(int i=1;i<=N;i++) cin>>A[i]; 42 for(int i=1;i<=M;i++) a[i]=0,b[i]=0;//清空的时候,注意M可能大于N,不能受上一组的数据影响 43 a[0]=1.0; 44 for(int i=1;i<=N;i++){ 45 for(int j=0;j<=M;j++){ 46 for(int k=0;k<=A[i];k++){ 47 if (j+k>M) continue; 48 b[j+k]+=a[j]*(1.0/F[k]); 49 // cout<<"j+k="<<j+k<<","<<b[j+k]<<endl; 50 } 51 } 52 for(int i=0;i<=M;i++) a[i]=b[i]; 53 for(int i=0;i<=M;i++) b[i]=0; 54 } 55 LL ans=(ceil)(a[M]*F[M]);//注意向上取整:因为除的时候除不尽,很小的尾数会丢失,然后再乘一个大数,可能会产生像6.999999这样的数。 56 cout<<ans<<endl; 57 } 58 return 0; 59 }
