图的基础---关键路径理解和实现(Java)

引言

    之前所说的拓扑排序是为了解决一个工程能否顺利进行的问题。但在生活中，我们还会经常遇到如何解决工程完成需要的最短时间问题。
    举个例子，我们需要制作一台汽车，我们需要先造各种各样的零件，然后进行组装，这些零件基本上都是在流水线上同时成产的。加入造一个轮子需要0.5天的时间，造一个发动机需要3天的时间，造一个车底盘需要2天的时间，造一个外壳需要2天的时间，其他零部件需要2天的时间，全部零部件集中到一个地方需要0.5天的时间，组装成车需要2天的时间，那么请问汽车厂造一辆车，最短需要多少时间。
    因为这些零部件都是分别在流水线上同时生产的，也就是说在生产发动机的这3天当中，可能已经生产了6个轮子，1.5个外壳，1.5个车底盘，而组装是在这些零部件都生产好之后才能进行，因此最短的时间就是零件生产时间最长的发动机3天+集中零部件0.5天+组成成车2天，以供需要5.5天完成一辆车的生产。
    所以，我们如果对一个流程获得最短时间，就需要分析它的拓扑关系，找到最关键的流程，这个流程的时间就是最短的时间。

AOE网的定义

在一个表示工程的带权有向图中，用顶点表示时间，用有向边表示活动，用边上的权值表示活动的持续时间，这种有向图的边表示活动的网，我们称之为AOE网。
把AOE网中没有入边的顶点称之为始点或源点，没有出边的顶点称之为终点或汇点。
摘自：《大话数据结构》

关键路径的定义

我们把路径上各个活动所持续的时间之和称之为路径长度，从源点到汇点具有最大的长度的路径叫做关键路径，在关键路径上的活动叫关键活动。
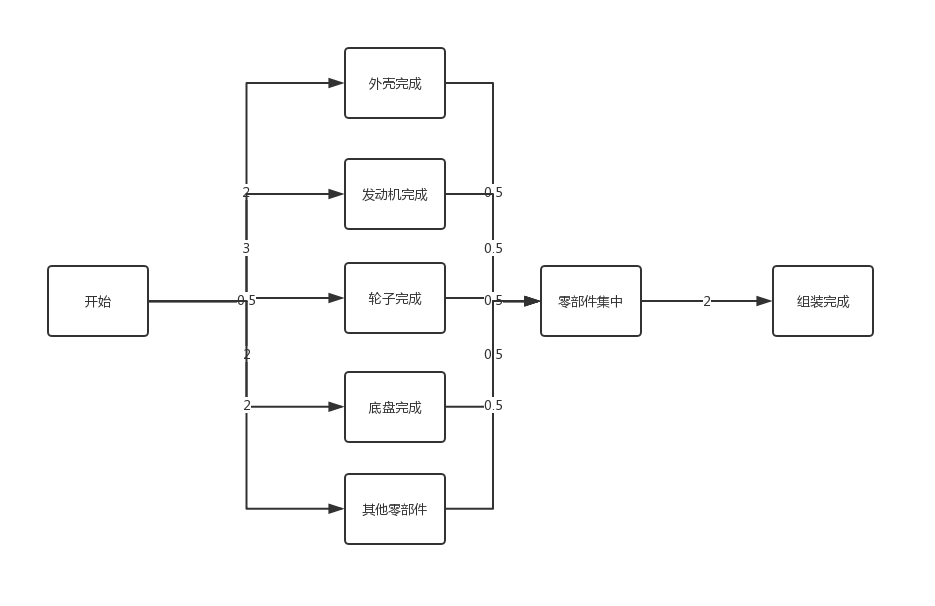
在这里插入图片描述
对上面的AOE网来说，其关键路径就是：开始->发动机完成->部件集中->组装完成。路径长度为5.5。

关键路径算法原理

对于一个活动来说，有活动的最早开始时间和最晚开始时间，比较这个活动的最早开始时间和最晚开始时间，如果最早开始时间和最晚开始时间相等，那么就意味着该活动是关键活动，活动间的路径为关键路径。如果不相等，那么这个活动就不是关键活动。

名词解释

事件的最早发生时间etv：即顶点 $v_k$ 的最早发生时间
事件的最晚发生时间ltv：即顶点 $v_k$ 的最晚发生时间，也就是每个顶点对应的事件最晚需要开始的时间，超过此时间将会延误整个工期。
活动的最早开工时间ete：即弧 $a_k$ 的最早发生时间
活动的最晚开工时间lte：即弧 $a_k$ 的最晚发生时间，也就是不推迟工期的最晚开工时间。

算法分析

    假设起点为 $v_0$ ，则我们从 $v_0$ 到 $v_i$ 的最长路径的长度为顶点(事件) $v_i$ 的最早发生时间。
    同时 $v_i$ 的最早发生时间也是所有以 $v_i$ 为尾的弧所表示的活动的最早开工时间(即ete)，
    定义活动最晚开工时间表示在不会延误所有工期(即lte)。通过根据ete[k]是否与lte[k]相等来判断 $a_k$ 是关键活动。
    同时，因为我们采用邻接表来存储AOE网，并且对于表示活动的每条边都具有活动的持续时间(即该边的权重)，所以，我们需要修改边表节点，增加一个weight来存储弧的权值。

首先我们要求顶点 $v_k$ 即求etv[k]的最早发生时间，公式：
$etv[k]= left {egin{array}{cc} 0, &当k=0时\ max[etv[i]+len<vi, vk>], & 当k不等于0且<vi, vk>属于P[k]时 end{array} ight.$
在计算ltv时，其实就是对拓扑序列倒过来进行，所以我们可以计算顶点 $v_k$ 即求ltv[k]的最晚发生时间。公式：
$ltv[k]= left {egin{array}{cc} etv[k], &当k=n-1时\ min[ltv[j]-len<vk, vj>], & 当k<n-1且<vk, vj>属于S[k]时 end{array} ight.$
这两个公式怎么理解呢
我的理解是，对于事件 $v_k$ 的最早发生时间，表现为以 $v_k$ 为弧头， $v_i$ 为弧尾的其他所有弧(注意：i的值可能没有，表示 $v_k$ 的入度为0；可能为n，表示 $v_k$ 的入度为n)的活动持续时间+ $v_i$ 的最早开工时间列表中的最大值。以上面的流程图为例，零部件集中这项事件只有等生产时间最长的发动机造好之后才能进行。
对于 $v_k$ 的最晚发生时间，表现为事件 $v_j$ 的最晚发生时间减去以 $v_k$ 为弧尾， $v_j$ 为弧头的其他所有弧(注意：j的值可能没有，表示 $v_k$ 的出度为0；可能为n，表示 $v_k$ 的出度为n)的活动持续时间。

求关键路径的步骤

根据图的描述建立该图的邻接表
从源点 $v_0$ 出发，根据拓扑序列算法求源点到汇点每个顶点的etv，如果得到的拓扑序列个数小于网的顶点个数，则该网中存在环，无关键路径，结束程序。
从汇点 $v_n$ 出发，且ltv[n-1]=etv[n-1]，按照逆拓扑序列，计算每个顶点的ltv。
根据每个顶点的etv和ltv求每条弧的ete和lte，若ete=lte，说明该活动是关键活动。

代码实现

示例AOE网：
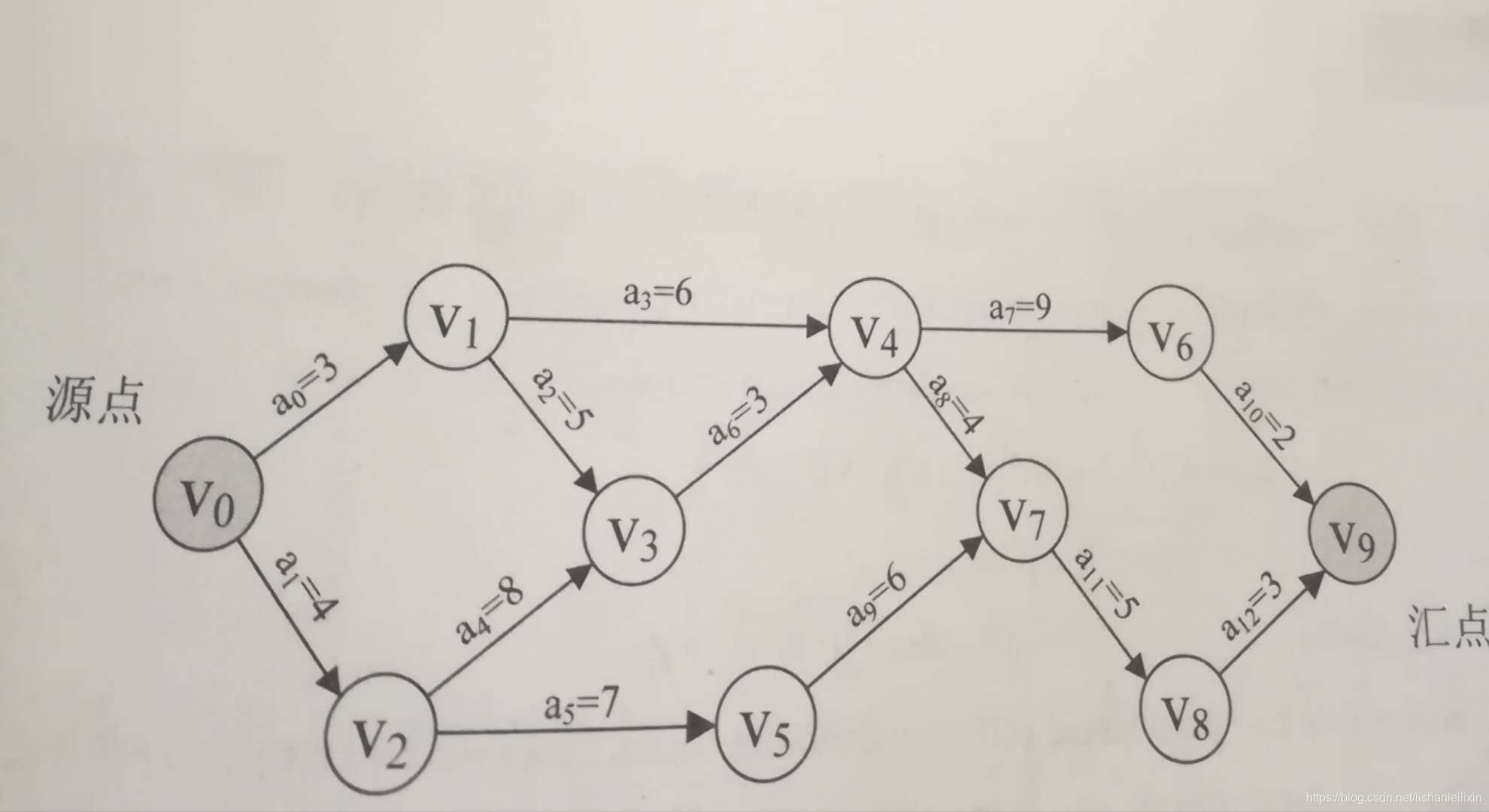
在这里插入图片描述
该网的邻接表结构：

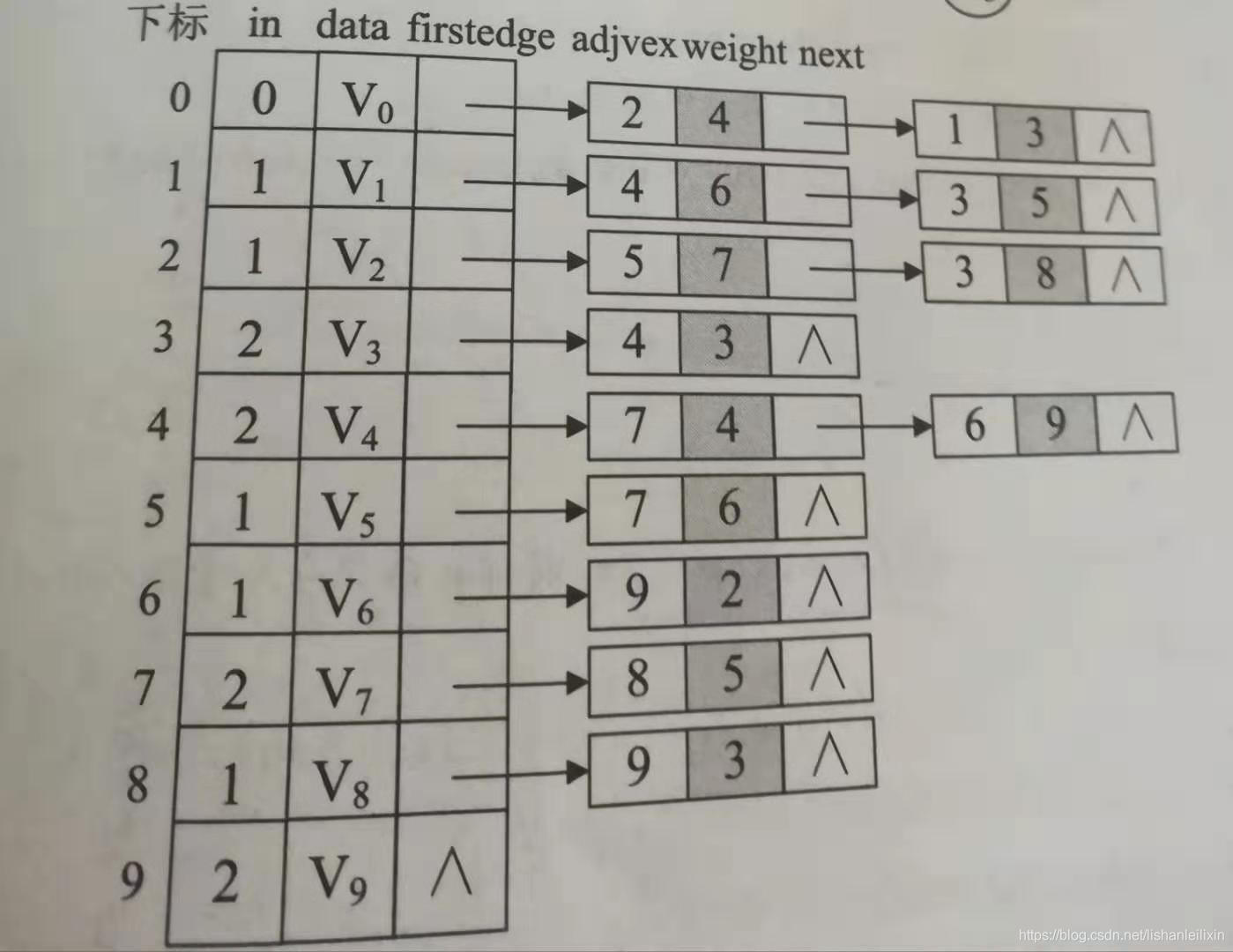
数据结构
边表节点：

public class EdgeNode {
	
	public int adjevex;
	public int weight;
	public EdgeNode next;
	
	public EdgeNode(int adjevex, EdgeNode next) {
		this.adjevex = adjevex;
		this.next = next;
	}
	
	public EdgeNode(int adjevex, int weight, EdgeNode next) {
		this.adjevex = adjevex;
		this.weight = weight;
		this.next = next;
	}
}

顶点节点：

public class VertexNode {

	public int in;
	public Object data;
	public EdgeNode firstedge;
	
	public VertexNode(Object data, int in, EdgeNode firstedge) {
		this.data = data;
		this.in = in;
		this.firstedge = firstedge;
	}
}

通过拓扑排序求得etv

	public boolean ToplogicalSort() {
		EdgeNode e;
		int k, gettop;
		int count = 0;
		etv = new int[adjList.length];
		for (int i = 0; i < adjList.length; i++) {
			if(adjList[i].in == 0) {
				stack.push(i);
			}
		}
		for (int i = 0; i < adjList.length; i++) {
			etv[i] = 0;
		}
		
		while(!stack.isEmpty()) {
			gettop = (int) stack.pop();
			count++;
			stack2.push(gettop);
			for (e = adjList[gettop].firstedge; e != null; e = e.next) {
				k = e.adjevex;
				if((--adjList[k].in) == 0) {
					stack.push(k);
				}
				if(etv[gettop] + e.weight > etv[k]) {
					etv[k] = etv[gettop] + e.weight;
				}
			}
		}
		if(count < adjList.length) return false;
		else return true;

	}

关键路径算法：

	public void CriticalPath() {
		EdgeNode e;
		int gettop, k, j;
		int ete, lte;
		if(!this.ToplogicalSort()) {
			System.out.println("该网中存在回路!");
			return;
		}
		ltv = new int[adjList.length];
		for (int i = 0; i < adjList.length; i++) {
			ltv[i] = etv[etv.length - 1];
		}
		
		while(!stack2.isEmpty()) {
			gettop = (int) stack2.pop();
			for(e = adjList[gettop].firstedge; e != null; e = e.next) {
				k = e.adjevex;
				if(ltv[k] - e.weight < ltv[gettop]) {
					ltv[gettop] = ltv[k] - e.weight;
				}
			}
		}
		for (int i = 0; i < adjList.length; i++) {
			for(e = adjList[i].firstedge; e != null; e = e.next) {
				k = e.adjevex;
				ete = etv[i];
				lte = ltv[k] - e.weight;
				if(ete == lte) {
					System.out.print("<" + adjList[i].data + "," + adjList[k].data + "> length: " + e.weight + ",");
				}
			}
		}
	}

完整代码：

public class CriticalPathSort {

	int[] etv, ltv;
	Stack stack = new Stack(); //存储入度为0的顶点，便于每次寻找入度为0的顶点时都遍历整个邻接表
	Stack stack2 = new Stack(); //将顶点序号压入拓扑序列的栈
	static VertexNode[] adjList;
	
	
	
	public boolean ToplogicalSort() {
		EdgeNode e;
		int k, gettop;
		int count = 0;
		etv = new int[adjList.length];
		for (int i = 0; i < adjList.length; i++) {
			if(adjList[i].in == 0) {
				stack.push(i);
			}
		}
		for (int i = 0; i < adjList.length; i++) {
			etv[i] = 0;
		}
		
		while(!stack.isEmpty()) {
			gettop = (int) stack.pop();
			count++;
			stack2.push(gettop);
			for (e = adjList[gettop].firstedge; e != null; e = e.next) {
				k = e.adjevex;
				if((--adjList[k].in) == 0) {
					stack.push(k);
				}
				if(etv[gettop] + e.weight > etv[k]) {
					etv[k] = etv[gettop] + e.weight;
				}
			}
		}
		if(count < adjList.length) return false;
		else return true;

	}
	
	
	public void CriticalPath() {
		EdgeNode e;
		int gettop, k, j;
		int ete, lte;
		if(!this.ToplogicalSort()) {
			System.out.println("该网中存在回路!");
			return;
		}
		ltv = new int[adjList.length];
		for (int i = 0; i < adjList.length; i++) {
			ltv[i] = etv[etv.length - 1];
		}
		
		while(!stack2.isEmpty()) {
			gettop = (int) stack2.pop();
			for(e = adjList[gettop].firstedge; e != null; e = e.next) {
				k = e.adjevex;
				if(ltv[k] - e.weight < ltv[gettop]) {
					ltv[gettop] = ltv[k] - e.weight;
				}
			}
		}
		for (int i = 0; i < adjList.length; i++) {
			for(e = adjList[i].firstedge; e != null; e = e.next) {
				k = e.adjevex;
				ete = etv[i];
				lte = ltv[k] - e.weight;
				if(ete == lte) {
					System.out.print("<" + adjList[i].data + "," + adjList[k].data + "> length: " + e.weight + ",");
				}
			}
		}
	}
	
	public static EdgeNode getAdjvex(VertexNode node) {
		EdgeNode e = node.firstedge;
		while(e != null) {
			if(e.next == null) break;
			else
				e = e.next;
		}
		return e;
	}
	public static void main(String[] args) {
		int[] ins = {0, 1, 1, 2, 2, 1, 1, 2, 1, 2};
		int[][] adjvexs = {
				{2, 1},
				{4, 3},
				{5, 3},
				{4},
				{7, 6},
				{7},
				{9},
				{8},
				{9},
				{}
		};
		int[][] widths = {
				{4, 3},
				{6, 5},
				{7, 8},
				{3},
				{4, 9},
				{6},
				{2},
				{5},
				{3},
				{}
		};
		adjList = new VertexNode[ins.length];
		for (int i = 0; i < ins.length; i++) {
			adjList[i] = new VertexNode("V"+i, ins[i],null);
			if(adjvexs[i].length > 0) {
				for (int j = 0; j < adjvexs[i].length; j++) {
					if(adjList[i].firstedge == null) 
						adjList[i].firstedge = new EdgeNode(adjvexs[i][j], widths[i][j], null);
					else {
						getAdjvex(adjList[i]).next = new EdgeNode(adjvexs[i][j], widths[i][j], null);
					} 	
				}
			}
		}
		
		CriticalPathSort c = new CriticalPathSort();
		c.CriticalPath();
		
	}
}

注意：这个例子中只有唯一一条关键路径，这并不表示不存在多条关键路径的有向无环图。如果是多条关键路径，则单是提高一条关键路径上的关键活动速度并不能导致整个工期缩短，而必须提高同时在几条关键路径上的活动的速度。