A*

A* 启发式搜索

 引言：

先前提到过的优先队列算法，每次都取出当前价值最小的值进行扩展，虽然已经大大的降低了复杂度，但也会有很多数据来卡你的复杂度；

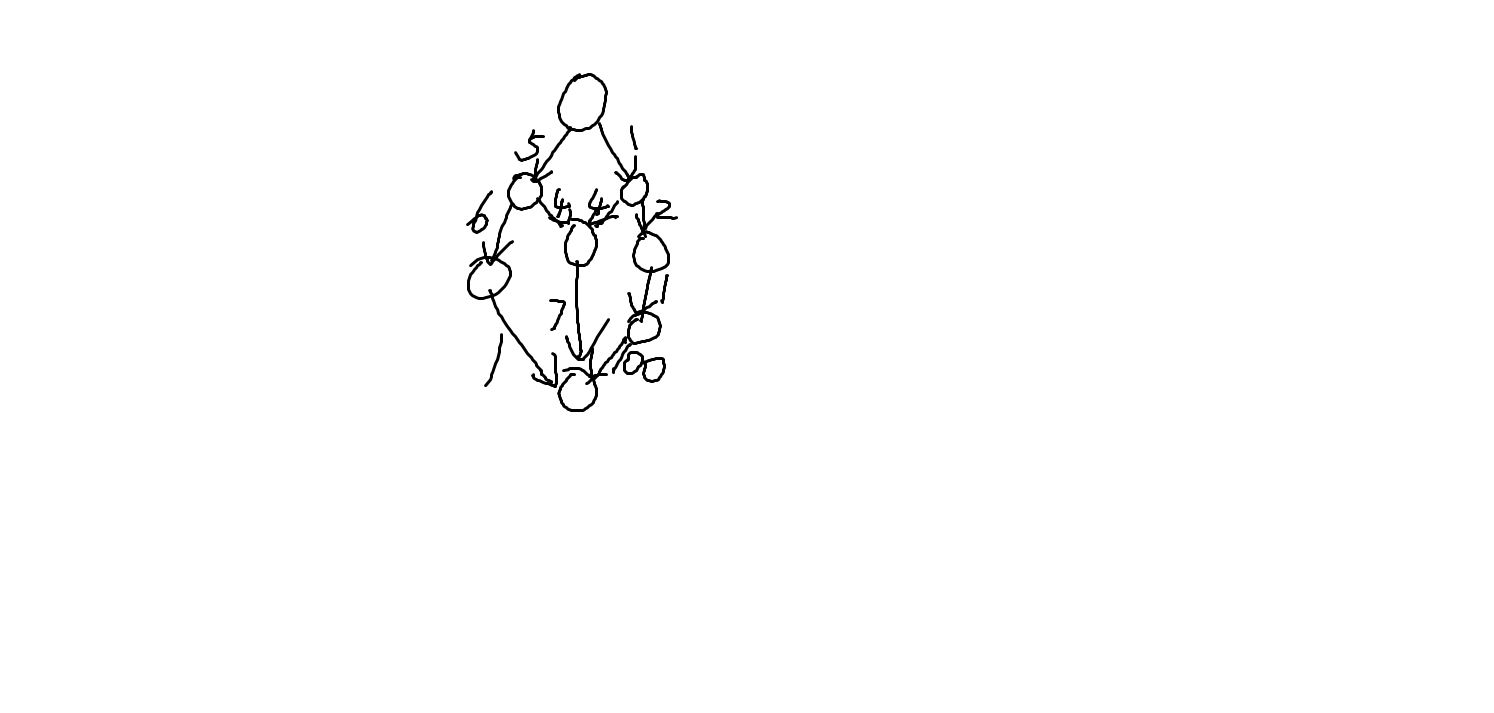
比如说上面这个图，我们会一直沿着右边这条路搜索，

然而最后我们发现一直沿着这条边搜索下去答案会变得很大，

这几次搜索就没什么用了；

最终答案为12；

在这样的基础上，我们可以对未来可能产生的情况进行预估；

设计了一个“估价函数”；

表示从该状态到目标状态的估计的价值；

用f（x）来表示估价函数；

用g（x）表示实际上从该状态到目标状态的价值

astar 的算法核心就是从堆中不断取出 [f(x)+当前代价] 的最小值进行扩展；

定理：

对于每一个当前状态 x

 有f(x)<=g(x)恒成立；

若不成立，正确答案无法得出；

举个例子：

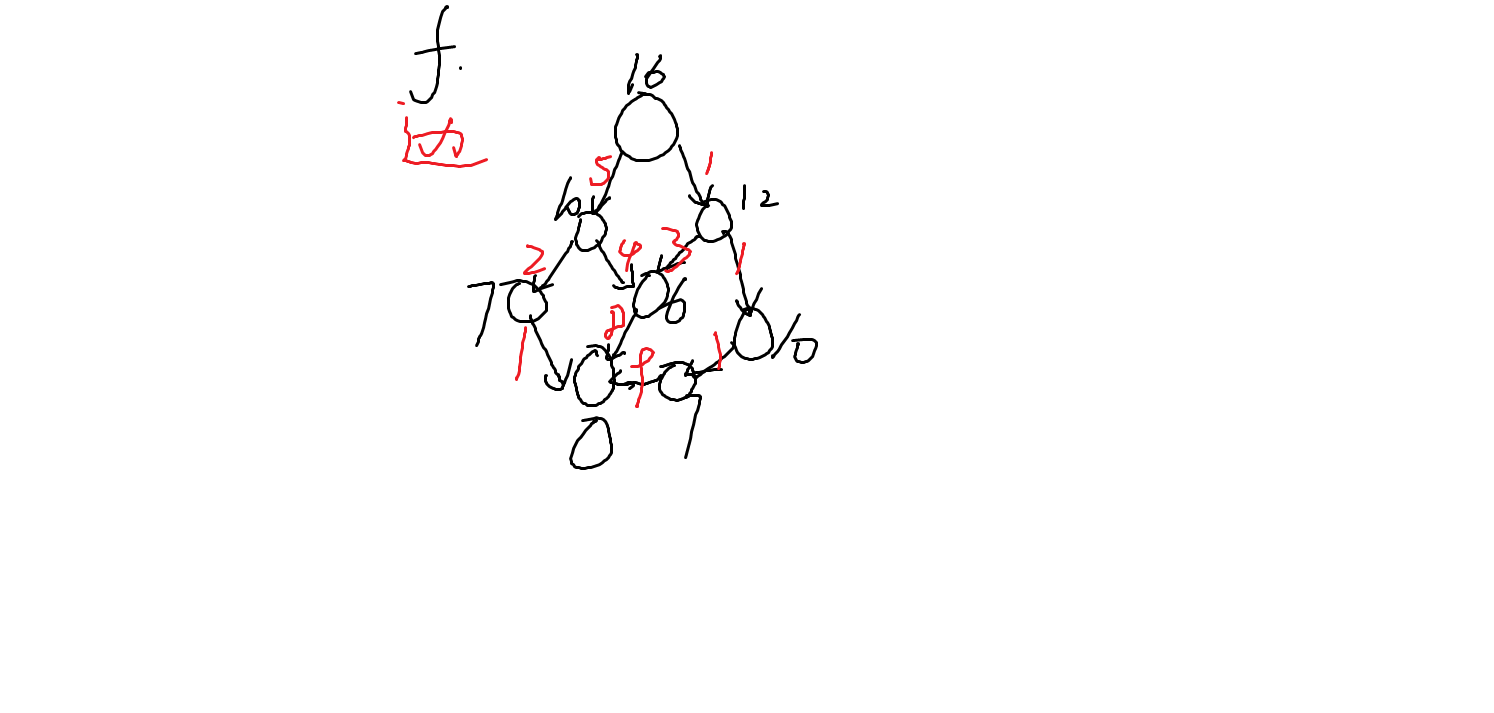
上图的数字代表着当前节点的f()值，也就是估计值，以及边权；

我们以更新最后一个答案来举一个例子：

红色代表着当前代价；

这时的

队列为： 3+7,4+6,5+10

取出：3+7;

得到12+0；插入队列；

此时队列为：4+6,12+0,5+10;

取出：4+6;

得到：12+0;

再次取出时，取出的值是12+0；

此时目标节点第一次被取出应为答案；

ans=12;

然而事实上这道题根据优先队列来做应该是 8

为最左端的一条路径；

由此可见当估价函数被错误地估计到了大于实际价值时，

我们的正解实际上是被压在堆里出不来；

根据设计估价函数小于实际代价：

假如某非最优解路径上的某一点s先被扩展；

那么，当目标节点被取出来前的某一时刻：

1、s为非最优解，所以s的当前代价大于从 start 到 end 的最小代价 minn；

2、状态 t 为最优解路径上的一个状态，就有 t状态代价+f(t) <= t当前代价+g(t) =minn;

所以s当前代价>t当前代价+f(t),t状态就会比s先扩展，从而找到最优解；

A* 算法的实质：

  带有估价的优先队列bfs；

例题 1：

第k短路

这个题目的大意是：给了一个n个点，m个边的图，求start 到 end的第k短路长度；

一个比较直观的做法是优先队列bfs

当一个状态被第一次取出时：我们可以得到从出态到此状态的最小代价；

推论：当一个状态被第i次取出时，对应的代价是start 到 此状态的第i短路；

所以当目标节点被第k次取出时，我们就得到了答案

我们用优先队列极有可能会超时，

所以我们使用astar 算法；

按照f()的设计准则，f（x）要小于等于实际的x到end的第k短距离；

所以我们可以设计f为当前节点x到end 的最短路

然后进行优先队列算法，当第k次取出时，即为答案；

怎样记录节点被取出呢？

我们可以用一个二元组pair<int,int> 。这时c++stl自带的一个组，可以把他想象成一个两个元素的结构体；

然后优先队列也用二元组定义；

#include <bits/stdc++.h>
using namespace std;
const int N = 1006;
int n, m, st, ed, k, f[N], cnt[N];
bool v[N];
vector<pair<int, int> > e[N], fe[N];
priority_queue<pair<int, int> > pq;

void dijkstra() {
    memset(f, 0x3f, sizeof(f));
    memset(v, 0, sizeof(v));
    f[ed] = 0;
    pq.push(make_pair(0, ed));
    while (pq.size()) {
        int x = pq.top().second;
        pq.pop();
        if (v[x]) continue;
        v[x] = 1;
        for (unsigned int i = 0; i < fe[x].size(); i++) {
            int y = fe[x][i].first, z = fe[x][i].second;
            if (f[y] > f[x] + z) {
                f[y] = f[x] + z;
                pq.push(make_pair(-f[y], y));
            }
        }
    }
}

void A_star() {
    if (st == ed) ++k;
    pq.push(make_pair(-f[st], st));
    memset(cnt, 0, sizeof(cnt));
    while (pq.size()) {
        int x = pq.top().second;
        int dist = -pq.top().first - f[x];
        pq.pop();
        ++cnt[x];
        if (cnt[ed] == k) {
            cout << dist << endl;
            return;
        }
        for (unsigned int i = 0; i < e[x].size(); i++) {
            int y = e[x][i].first, z = e[x][i].second;
            if (cnt[y] != k) pq.push(make_pair(-f[y] - dist - z, y));
        }
    }
    cout << "-1" << endl;
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int x, y, z;
        scanf("%d %d %d", &x, &y, &z);
        e[x].push_back(make_pair(y, z));
        fe[y].push_back(make_pair(x, z));
    }
    cin >> st >> ed >> k;
    dijkstra();
    A_star();
    return 0;
}

因为我们加上了一个估价函数，我们的实际时间复杂度被大大降低，能够快速求出结果。

例题2：

 八数码 （无可解性判断）（有可解性判断）

先讲有解时的移动方法：

问题有解时，我们可以采用astar算法搜索一种移动步数最少的方案；

我们可以发现，每次移动是将空格与一个数字换一个位置；

至多每次将一个数字朝他的目标位置移动一格；、

所以即使每个数字的移动都是有意义的，

在一个状态x，从 此状态到目标状态的总步数 不可能小于 所有数字从此状态到目标状态的曼哈顿距离之和；

所以，我们的估价函数f就可以设为 ：所有数字从此状态到目标状态的曼哈顿距离之和；

即：for(num=1->9) f(x)+=abs(x_a_num-end_a_num)+abs(x_b_num-end_b_num) 

然后进行优先队列搜索；

可行解判断：

 奇数码问题：奇数码两个局面可以互相达到，当且仅当，

两个局面的数字写成一列后（空格不算），逆序对的奇偶性相同；

必要性证明：

 空格左右移动时，写出来的序列相同；

空格上下移动时，相当于某个数与它前后的n-1个数交换了位置，

n-1为一个偶数，所以逆序对的变化个数也是偶数。

所以八数码问题就是一个n=3的奇数码问题；

只需要判断前后状态的逆序对奇偶就能判断是否有解了；

这里放出的是没有用逆序对判断的代码，比起用判断可能时间较大；

#include<bits/stdc++.h>
using namespace std;
// state：八数码的状态(3*3九宫格压缩为一个整数)
// dist：当前代价 + 估价
struct rec{int state,dist;
    rec(){}
    rec(int s,int d){state=s,dist=d;}
};
int a[3][3];

map<int,int> d,f,go;
priority_queue<rec> q;
const int dx[4]={-1,0,0,1},dy[4]={0,-1,1,0};
char dir[4]={'u','l','r','d'};

bool operator <(rec a,rec b) {
    return a.dist>b.dist;
}

// 把3*3的九宫格压缩为一个整数（9进制）
int calc(int a[3][3]) {
    int val=0;
    for(int i=0;i<3;i++)
        for(int j=0;j<3;j++) {
            val=val*9+a[i][j];
        }
    return val;
}

// 从一个9进制数复原出3*3的九宫格，以及空格位置
pair<int,int> recover(int val,int a[3][3]) {
    int x,y;
    for(int i=2;i>=0;i--)
        for(int j=2;j>=0;j--) {
            a[i][j]=val%9;
            val/=9;
            if(a[i][j]==0) x=i,y=j;
        }
    return make_pair(x,y);
}

// 计算估价函数
int value(int a[3][3]) {
    int val=0;
    for(int i=0;i<3;i++)
        for(int j=0;j<3;j++) {
            if(a[i][j]==0) continue;
            int x=(a[i][j]-1)/3;
            int y=(a[i][j]-1)%3;
            val+=abs(i-x)+abs(j-y);
        }
    return val;
}

// A*算法
int astar(int sx,int sy,int e) {
    d.clear(); f.clear(); go.clear();
    while(q.size()) q.pop();
    int start=calc(a);
    d[start]=0;
    q.push(rec(start,0+value(a)));
    while(q.size()) {
        // 取出堆顶
        int now=q.top().state; q.pop();
        // 第一次取出目标状态时，得到答案
        if(now==e) return d[now];
        int a[3][3];
        // 复原九宫格
        pair<int,int> space=recover(now,a);
        //空格位置 
        int x=space.first,y=space.second;
        // 枚举空格的移动方向（上下左右）
        for(int i=0;i<4;i++) {
            int nx=x+dx[i], ny=y+dy[i];
            if (nx<0||nx>2||ny<0||ny>2) continue;
            swap(a[x][y],a[nx][ny]);
            int next=calc(a);
            // next状态没有访问过，或者能被更新
            if(d.find(next)==d.end()||d[next]>d[now]+1) {
                d[next]=d[now]+1;
                // f和go记录移动的路线，以便输出方案
                f[next]=now;
                go[next]=i;
                // 入堆
                q.push(rec(next,d[next]+value(a)));
            }
            swap(a[x][y],a[nx][ny]);//回溯 
        }
    }
    return -1;
}

void print(int e) {
    if(f.find(e)==f.end()) return;
    print(f[e]);
    putchar(dir[go[e]]);
}

int main() {
    int end=0;
    for(int i=1;i<=8;i++) end=end*9+i;
    end*=9;
    int x,y;
    for(int i=0;i<3;i++)
        for(int j=0;j<3;j++) {
            char str[2];
            scanf("%s",str);
            if(str[0]=='x') a[i][j]=0,x=i,y=j;
            else a[i][j]=str[0]-'0';
        }
    int ans=astar(x,y,end);
    if(ans==-1) puts("unsolvable"); else print(end);
    return 0; 
}