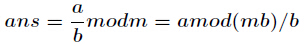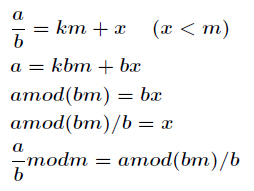这个不能直接求逆元来做,
a存在模p的乘法逆元的充要条件是gcd(a,p) = 1,有很多gcd(a,9901)不是1的,所以不能用p-1的mod-2次幂
求现在来看一个逆元最常见问题,求如下表达式的值
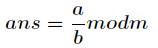
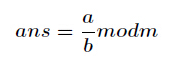
当然这个经典的问题有很多方法,最常见的就是扩展欧几里得,如果
但是你会发现费马小定理和扩展欧几里得算法求逆元是有局限性的,它们都会要求a

种通用的求逆元方法,适合所有情况。公式如下
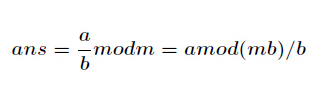
在这里有两种方法求1.可以用二分的方法求等比数列的前N项和
若n为奇数,一共有偶数项
1+p+p^2+.....+p^n=(1+p^(n/2+1))+p*(1+p^(n/2+1))+p^2*(1+p^(n/2+1))+.....+p^(n/2)*(1+p^(n/2+1))=(1+p+p^2+....+p^(n/2))*(1+p^(n/2+1))
若n为偶数,一共有奇数项
1+p+p^2+.....+p^n=(1+p^(n/2+1))+p*(1+p^(n/2+1))+p^2(1+p^(n/2+1))+.....+p^(n/2-1)*(1+p^(n/2+1))+p^(n/2)=(1+p+p^2+.....+p^(n/2-1))*(1+p^(n/2+1)+p^(n/2);
long long sum(long long p,long long n) { if(n==0) return 1; if(n%2) return (sum(p,n/2)*(1+power(p,n/2+1)))%mod; else return (sum(p,n/2-1)*(1+power(p,n/2+1))+power(p,n/2))%mod; }
AC代码:
#include<iostream> #include<algorithm> using namespace std; typedef long long ll; const int maxn=1e6+100; const ll mod=9901; ll a,b; ll qpow(ll a,ll b){ ll ans=1; while(b){ if(b&1){ ans=(ans*a)%mod; } a=(a*a)%mod; b/=2; } return ans%mod; } ll sum(ll p,ll k){//1+p^1+p^2+....p^k if(k==0){ return 1; } if(k&1){//k为奇数 return ((1+qpow(p,k/2+1))*sum(p,k/2))%mod; } else{//k为偶数 return ((1+qpow(p,k/2+1))*sum(p,k/2-1)+qpow(p,k/2))%mod; } } ll cal(){ ll ans=1; int z; for(ll i=2;i*i<=a;i++){ z=0; while(a%i==0){ a/=i; z++; } ans=(ans*sum(i,z*b))%mod; } if(a!=1){ ans=(ans*sum(a,b))%mod; } return ans%mod; } int main(){ while(~scanf("%lld%lld",&a,&b)){ printf("%lld ",cal()); } return 0; }
方法二:
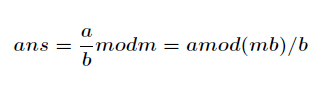
因为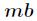
#include <iostream> #include <string.h> #include <stdio.h> using namespace std; typedef long long LL; const int N = 10005; const int MOD = 9901; bool prime[N]; int p[N]; int cnt; void isprime() { cnt = 0; memset(prime,true,sizeof(prime)); for(int i=2; i<N; i++) { if(prime[i]) { p[cnt++] = i; for(int j=i+i; j<N; j+=i) prime[j] = false; } } } LL multi(LL a,LL b,LL m) { LL ans = 0; a %= m; while(b) { if(b & 1) { ans = (ans + a) % m; b--; } b >>= 1; a = (a + a) % m; } return ans; } LL quick_mod(LL a,LL b,LL m) { LL ans = 1; a %= m; while(b) { if(b & 1) { ans = multi(ans,a,m); b--; } b >>= 1; a = multi(a,a,m); } return ans; } void Solve(LL A,LL B) { LL ans = 1; for(int i=0; p[i]*p[i] <= A; i++) { if(A % p[i] == 0) { int num = 0; while(A % p[i] == 0) { num++; A /= p[i]; } LL M = (p[i] - 1) * MOD; ans *= (quick_mod(p[i],num*B+1,M) + M - 1) / (p[i] - 1); ans %= MOD; } } if(A > 1) { LL M = MOD * (A - 1); ans *= (quick_mod(A,B+1,M) + M - 1) / (A - 1); ans %= MOD; } cout<<ans<<endl; } int main() { LL A,B; isprime(); while(cin>>A>>B) Solve(A,B); return 0; }